Incident angle-tuned filter based on 1D resonant waveguide grating in full conical mounting
doi: 10.37188/CO.EN-2023-0030
-
摘要:
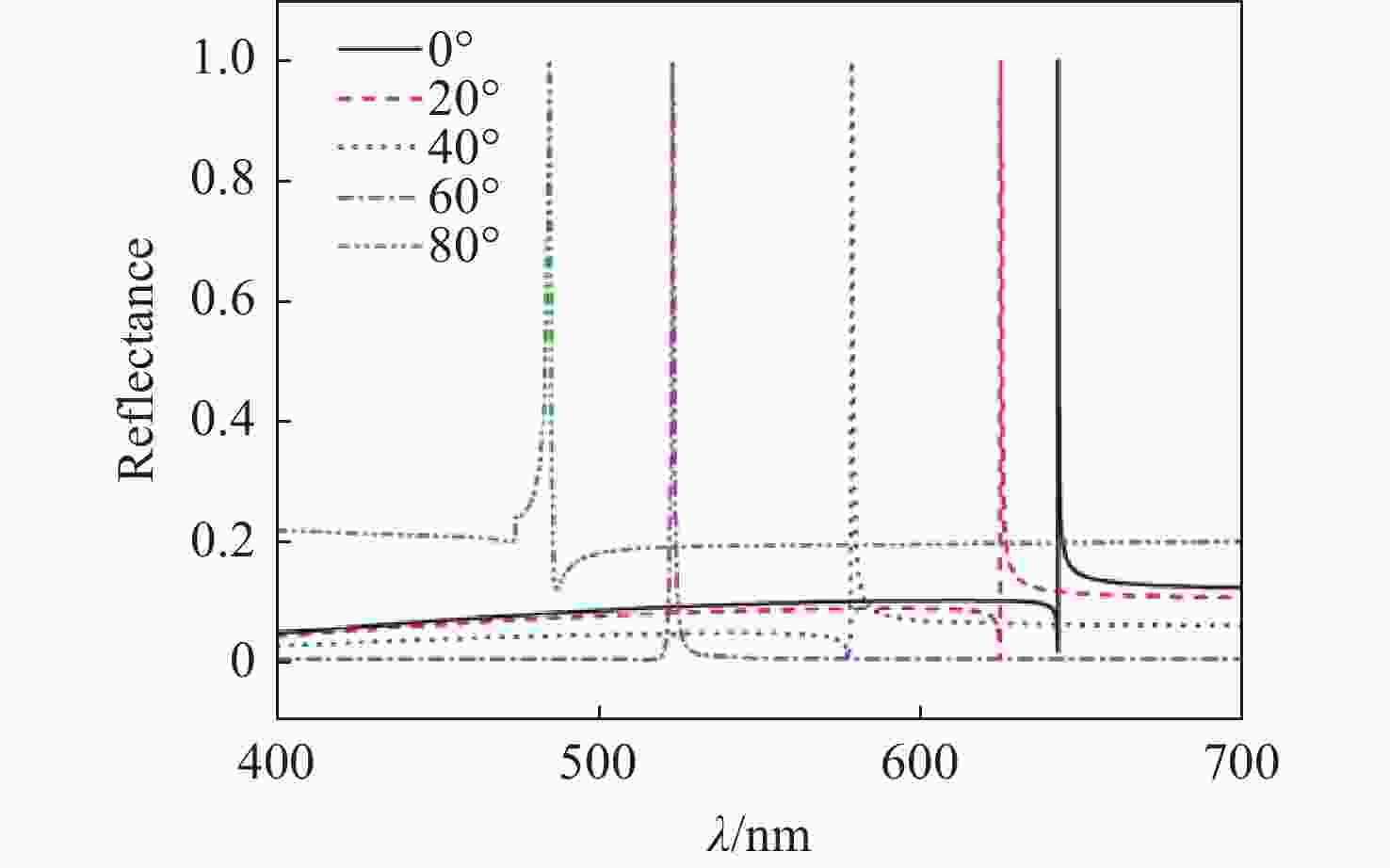
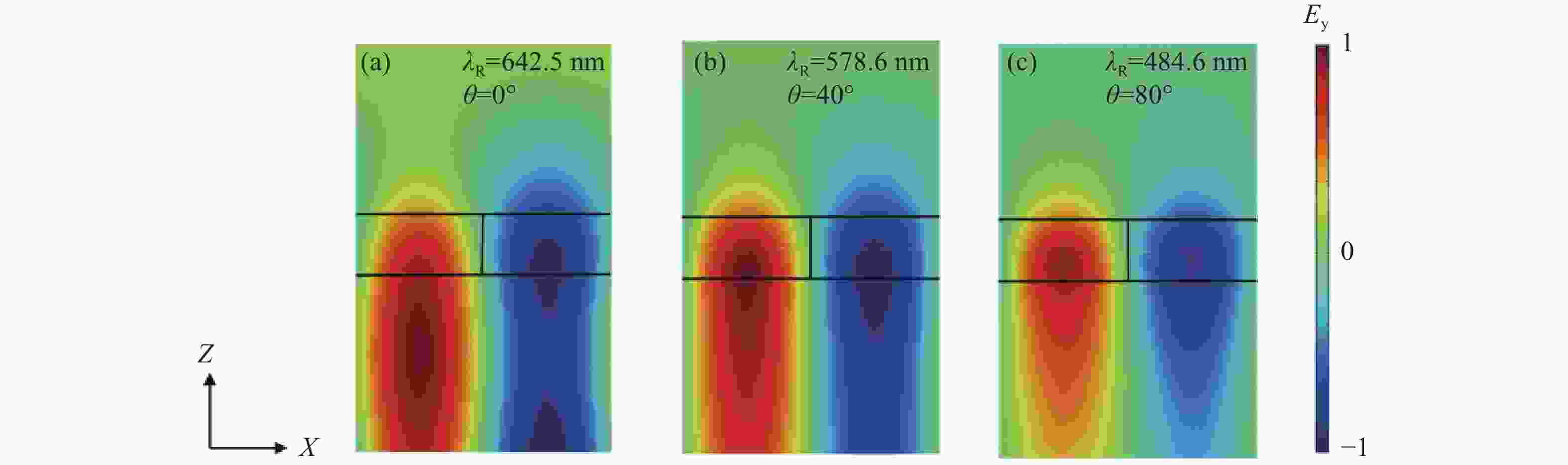
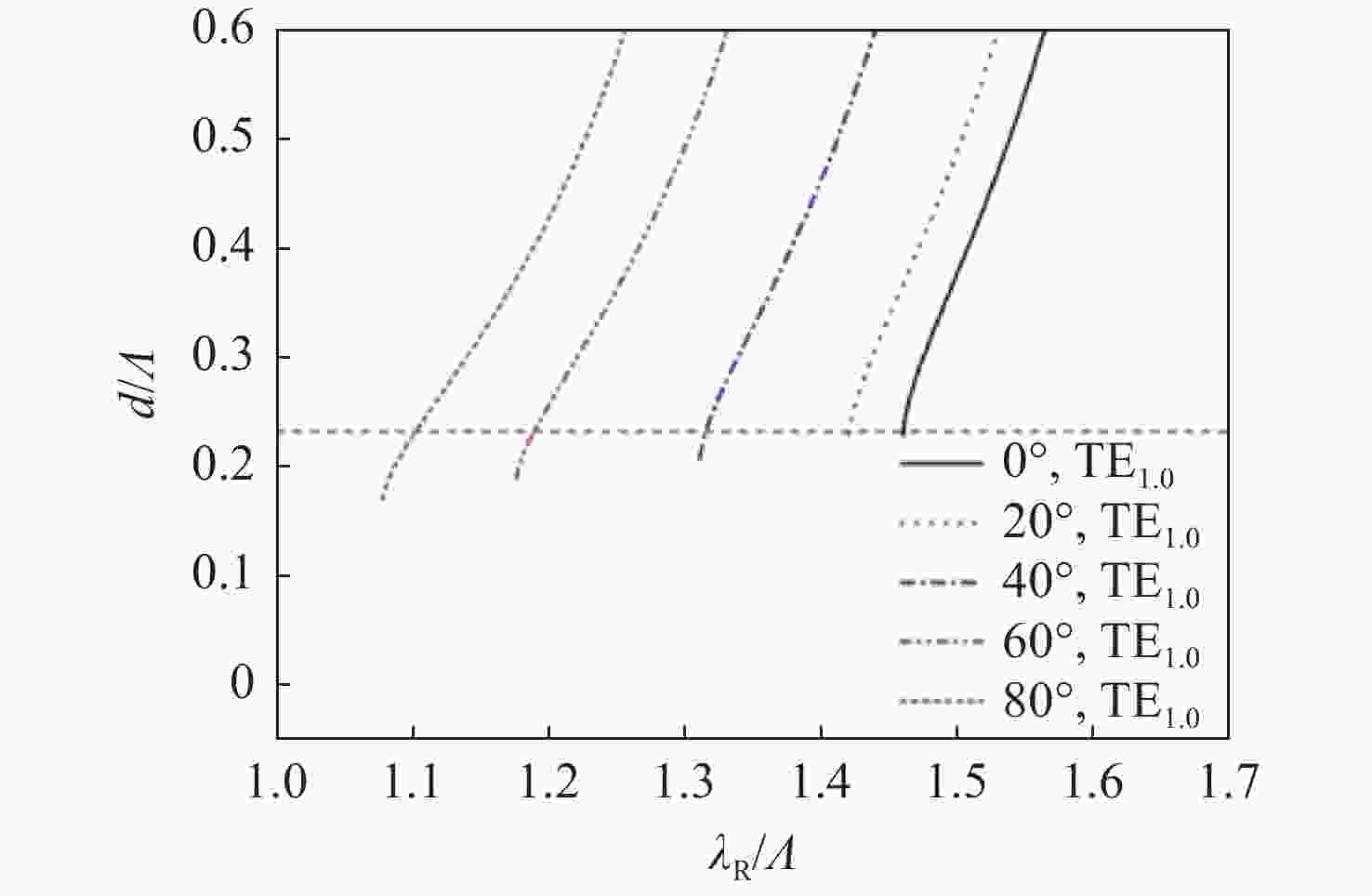
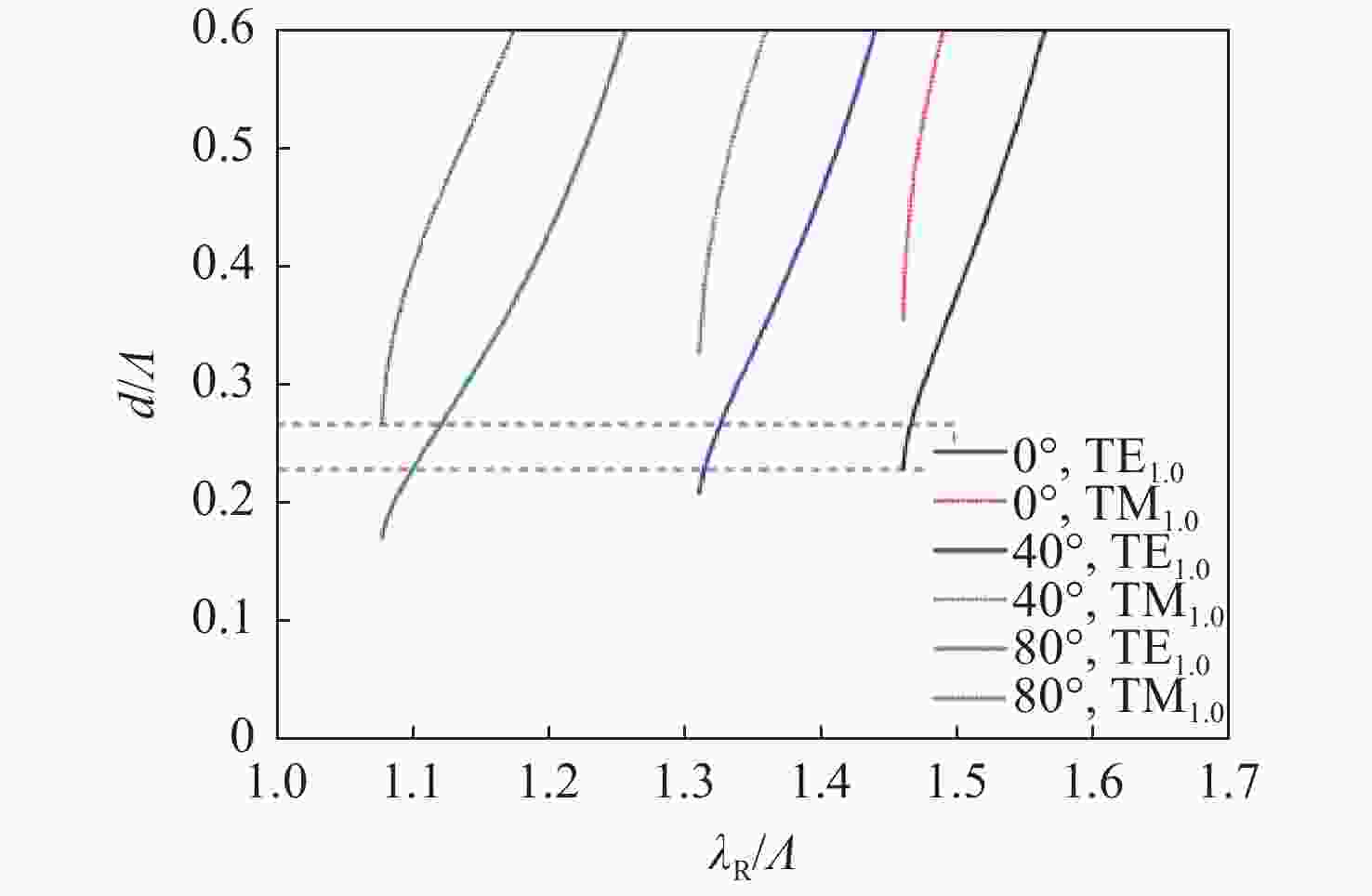
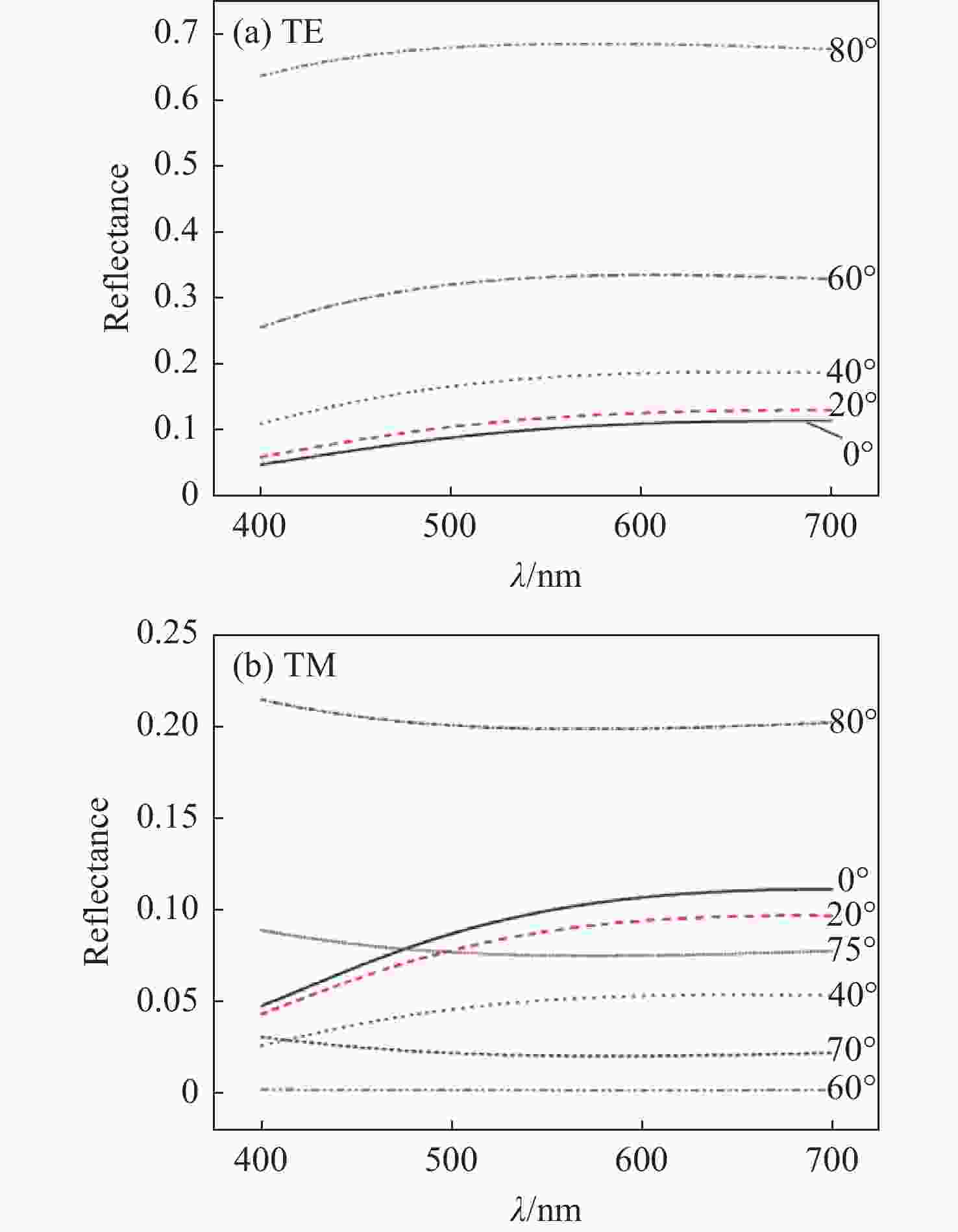
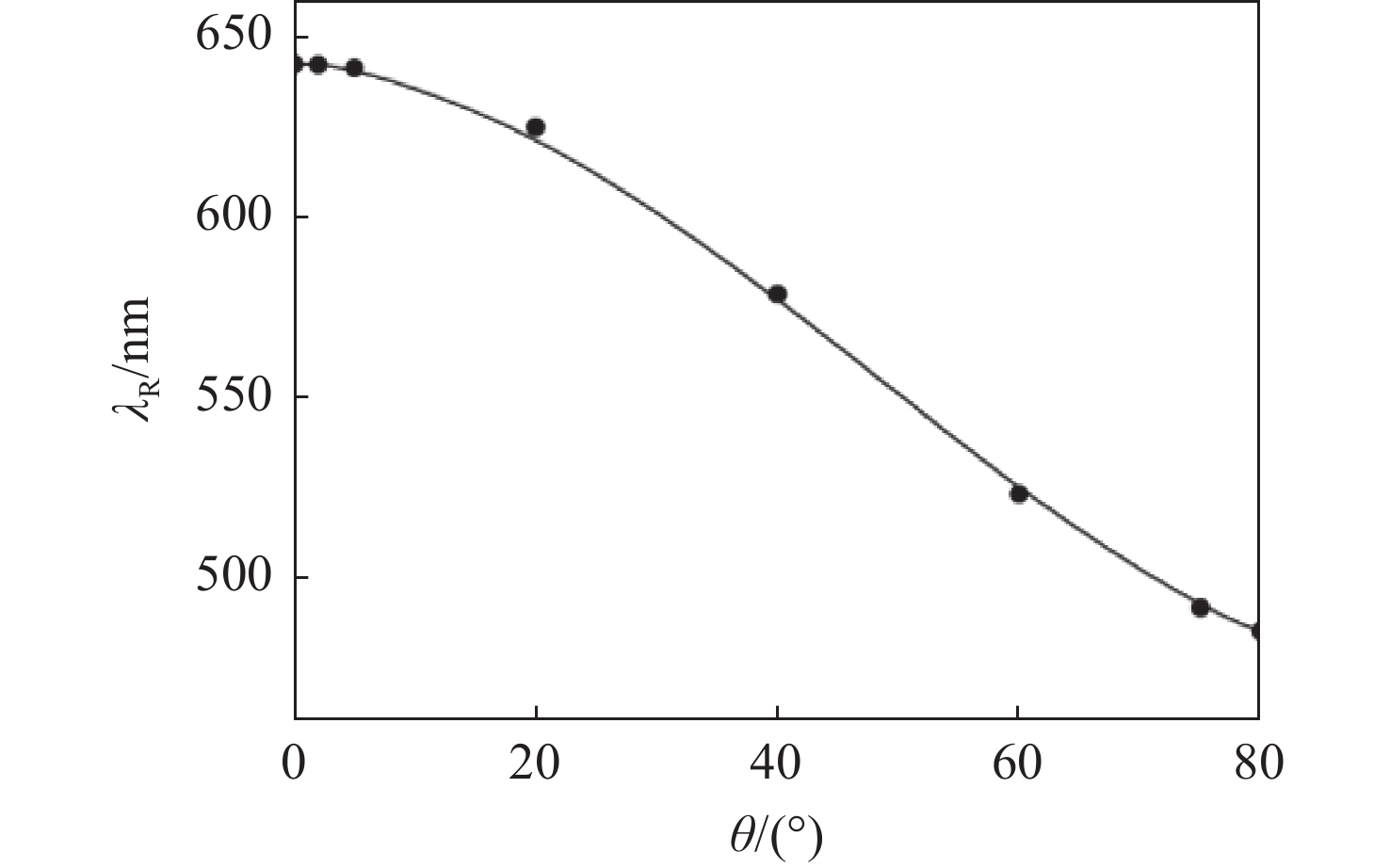
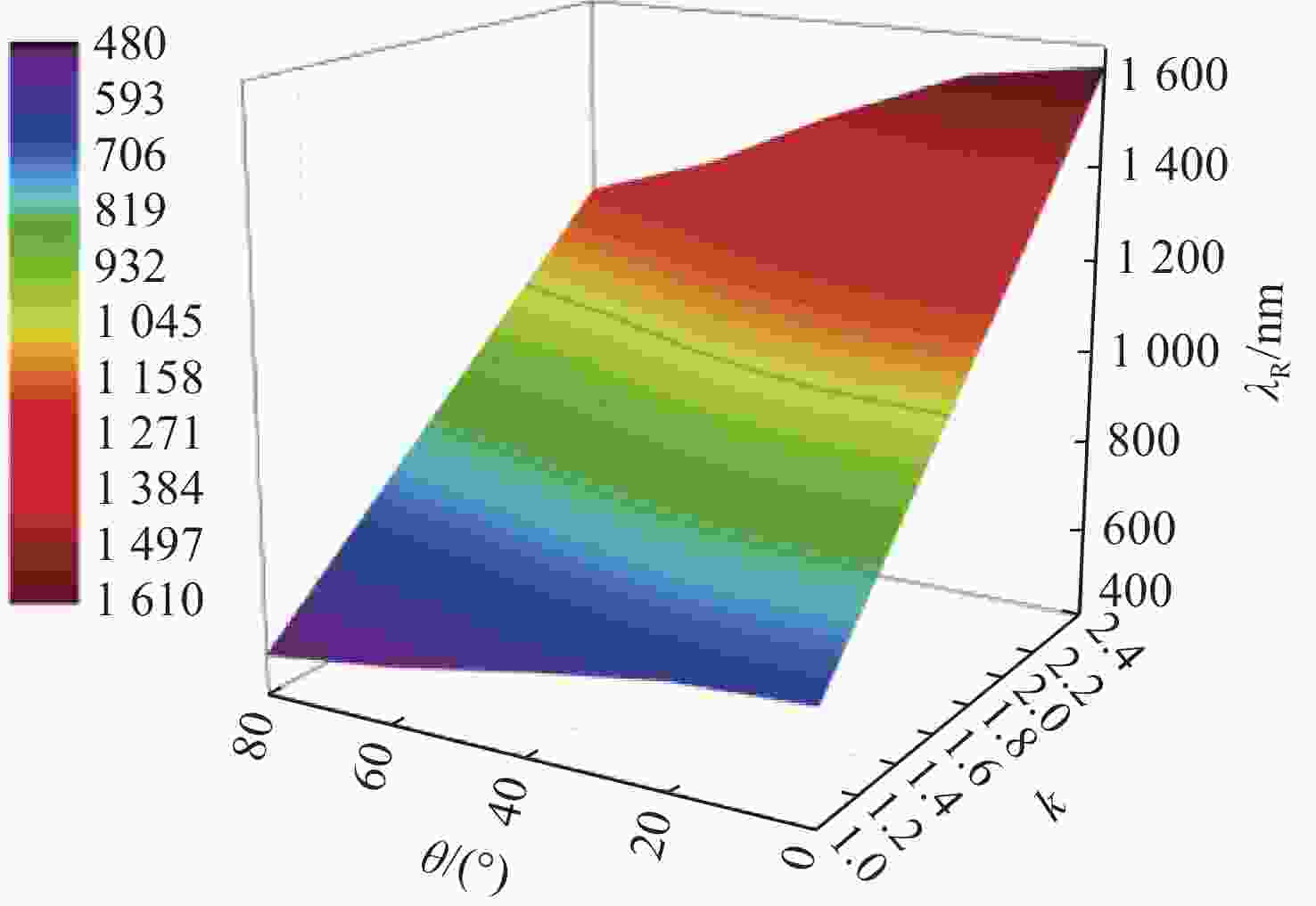
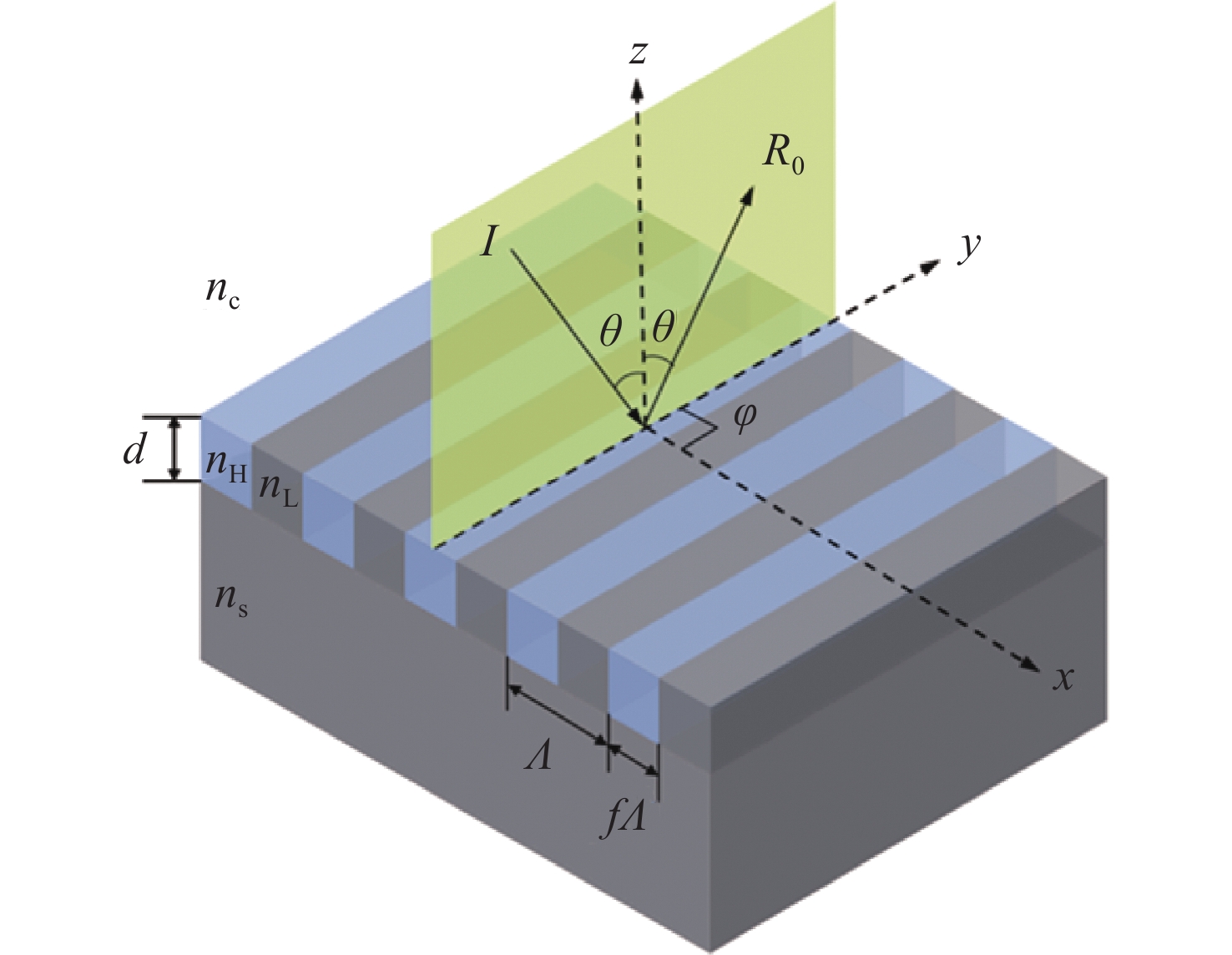
本文提出并展示了一种全圆锥入射下基于一维共振波导光栅的入射角调谐滤波器。通过优化光栅层厚度，使其能够在支持TE导模的同时抑制TM导模。本文设计的滤波器呈现出可调谐的单一反射峰, 峰值反射率理论上可达100%。当入射角改变时，共振波长可以由642.5 nm调节至484.6 nm。该反射峰是由一级衍射波与TE导模（基模）之间的共振效应所产生的。同样地，通过按比例增加光栅层的厚度和周期可实现应用于更高动态范围的可调谐滤波器。
Abstract:This paper proposes and demonstrates a tunable filter using full conical mounting. The designed 1D resonant waveguide grating presents a tunable single reflection peak. The peak reflectance can theoretically reach 100%. The resonant wavelength can be tuned from 642.5 nm to 484.6 nm by changing the incident angle. The resonance between the 1st-order diffracted wave and fundamental transverse electric (TE) guided mode generates the reflection peak. This feature was achieved by optimizing the grating thickness to support the TE guided mode and suppress the transverse magnetic (TM) guided mode. The same concept can be applied to tunable filters with high dynamic range by increasing the thickness and period of grating in equal proportion.
-
Key words:
- tunable filters /
- resonant waveguide gratings /
- incident angle /
- full conical mounting
-
Figure 1. Schematic diagram of 1D RWG in full conical mounting. The structural parameters are nH = 1.8, nL = 1.63, ns = 1.46, nc = 1.0, d = 102 nm, f = 0.5, and Λ = 440 nm
Figure 2. Calculated reflection spectra with the incident angle variation when the TM-polarized wave irradiates 1D RWG in full conical mounting
Figure 3. Internal electric field (Ey) profile for (a) λR = 642.5 nm (θ = 0°); (b) λR = 578.6 nm (θ = 40°); (c) λR = 484.6 nm (θ = 80°)
Figure 4. Calculated resonant positions based on the eigenvalue equation of fundamental TE guided mode at different incident angles
Figure 5. Calculated resonant positions based on the eigenvalue equation of fundamental TE and TM guided modes at different incident angles
Figure 6. Reflection spectra of equivalent multilayer stacks at different incident angles. (a) TE-polarized incidence; (b) TM-polarized incidence
-
[1] FENG S Q, LIU T T, CHEN W Y, et al. Enhanced sum-frequency generation from etchless lithium niobate empowered by dual quasi-bound states in the continuum[J]. Science China Physics, Mechanics & Astronomy, 2023, 66(12): 124214. [2] WU F, WU J J, GUO ZH W, et al. Giant enhancement of the Goos-Hänchen shift assisted by quasibound states in the continuum[J]. Physical Review Applied, 2019, 12(1): 014028. doi: 10.1103/PhysRevApplied.12.014028 [3] QIAN L Y, WANG K N, ZHU W, et al. Enhanced sensing ability in a single-layer guided-mode resonant optical biosensor with deep grating[J]. Optics Communications, 2019, 452: 273-280. doi: 10.1016/j.optcom.2019.07.047 [4] HSU H Y, LAN Y H, HUANG CH SH. A gradient grating period guided-mode resonance spectrometer[J]. IEEE Photonics Journal, 2018, 10(1): 4500109. [5] FEHREMBACH A L, SHARSHAVINA K, LEMARCHAND F, et al. 2 × 1D crossed strongly modulated gratings for polarization independent tunable narrowband transmission filters[J]. Journal of the Optical Society of America A, 2017, 34(2): 234-240. doi: 10.1364/JOSAA.34.000234 [6] QIAN L Y, ZHU W, WANG K N, et al. Polarization-controlled reflectance tunable narrow-band filter with single channel based on sparse dielectric grating[J]. Optics Communications, 2019, 443: 123-128. doi: 10.1016/j.optcom.2019.03.010 [7] KUO W K, HSU C J. Two-dimensional grating guided-mode resonance tunable filter[J]. Optics Express, 2017, 25(24): 29642-29649. doi: 10.1364/OE.25.029642 [8] FERRARO A, TANGA A A, ZOGRAFOPOULOS D C, et al. Guided mode resonance flat-top bandpass filter for terahertz telecom applications[J]. Optics Letters, 2019, 44(17): 4239-4242. doi: 10.1364/OL.44.004239 [9] SAKAT E, VINCENT G, GHENUCHE P, et al. Free-standing guided-mode resonance band-pass filters: from 1D to 2D structures[J]. Optics Express, 2012, 20(12): 13082-13090. doi: 10.1364/OE.20.013082 [10] SALEEM M R, ZHENG D D, BAI B F, et al. Replicable one-dimensional non-polarizing guided mode resonance gratings under normal incidence[J]. Optics Express, 2012, 20(15): 16974-16980. doi: 10.1364/OE.20.016974 [11] FANG CH L, DAI B, LI ZH, et al. Tunable guided-mode resonance filter with a gradient grating period fabricated by casting a stretched PDMS grating wedge[J]. Optics Letters, 2016, 41(22): 5302-5305. doi: 10.1364/OL.41.005302 [12] FENG SH F, ZHANG X P, SONG J Y, et al. Theoretical analysis on the tuning dynamics of the waveguide-grating structures[J]. Optics Express, 2009, 17(2): 426-436. doi: 10.1364/OE.17.000426 [13] CHAUDHURI R R, ENEMUO A N, SONG Y, et al. Polymer based resonant waveguide grating photonic filter with on-chip thermal tuning[J]. Optics Communications, 2018, 418: 1-9. doi: 10.1016/j.optcom.2018.02.045 [14] WANG C T, HOU H H, CHANG P C, et al. Full-color reflectance-tunable filter based on liquid crystal cladded guided-mode resonant grating[J]. Optics Express, 2016, 24(20): 22892-22898. doi: 10.1364/OE.24.022892 [15] UDDIN M J, MAGNUSSON R. Efficient guided-mode-resonant tunable color filters[J]. IEEE Photonics Technology Letters, 2012, 24(17): 1552-1554. doi: 10.1109/LPT.2012.2208453 [16] COVES Á, GIMENO B, ANDRÉS M V. Oblique incidence and polarization effects in coupled gratings[J]. Optics Express, 2012, 20(23): 25454-25460. doi: 10.1364/OE.20.025454 [17] YUKINO R, SAHOO P K, SHARMA J, et al. Wide wavelength range tunable one-dimensional silicon nitride nano-grating guided mode resonance filter based on azimuthal rotation[J]. AIP Advances, 2017, 7(1): 015313. doi: 10.1063/1.4975344 [18] REN ZH B, SUN Y H, HU J SH, et al. Nonpolarizing guided-mode resonance filter with high tolerance of conical angle[J]. Journal of Optics, 2018, 20(8): 085601. doi: 10.1088/2040-8986/aacdd6 [19] WANG D Y, WANG Q K, WU M T. Spectral characteristics of a guided mode resonant filter with planes of incidence[J]. Applied Optics, 2018, 57(27): 7793-7797. doi: 10.1364/AO.57.007793 [20] WANG W, CAI W, SHI ZH, et al. Polarization-insensitive one-dimensional guided-mode resonance filter operating at conical mounting[J]. Optics Letters, 2018, 43(21): 5226-5229. doi: 10.1364/OL.43.005226 [21] KODALI A K, SCHULMERICH M, IP J, et al. Narrowband midinfrared reflectance filters using guided mode resonance[J]. Analytical Chemistry, 2010, 82(13): 5697-5706. doi: 10.1021/ac1007128 [22] LI Y Y, HU CH, WU Y CH, et al. Numerical investigation of one-dimensional nonpolarizing guided-mode resonance gratings with conformal dielectric films[J]. Optics Express, 2013, 21(1): 345-357. doi: 10.1364/OE.21.000345 [23] FAN L N, JIA K H, MA J SH. Transmission filter controlled by incident conditions in single-layer waveguide grating structures[J]. Applied Optics, 2019, 58(31): 8371-8375. doi: 10.1364/AO.58.008371 [24] WANG D Y, WANG Q K, LIU D M. Polarization-insensitive filter for incidence between classic and full conical mountings[J]. IEEE Photonics Technology Letters, 2018, 30(5): 495-498. doi: 10.1109/LPT.2018.2799950 [25] LACOUR D, GRANET G, PLUMEY J P, et al. Polarization independence of a one-dimensional grating in conical mounting[J]. Journal of the Optical Society of America A, 2003, 20(8): 1546-1552. doi: 10.1364/JOSAA.20.001546 [26] MOHARAM M G, GAYLORD T K. Diffraction analysis of dielectric surface-relief gratings[J]. Journal of the Optical Society of America, 1982, 72(10): 1385-1392. doi: 10.1364/JOSA.72.001385 [27] MAGNUSSON R, WANG S S. New principle for optical filters[J]. Applied Physics Letters, 1992, 61(9): 1022-1024. doi: 10.1063/1.107703 [28] WANG S S, MAGNUSSON R. Theory and applications of guided-mode resonance filters[J]. Applied Optics, 1993, 32(14): 2606-2613. doi: 10.1364/AO.32.002606 -
下载:
计量
- 文章访问数: 412
- HTML全文浏览量: 106
- PDF下载量: 217
- 被引次数: 0
