A photoacoustic tomography image reconstruction method based on forward imaging model
-
摘要:
在光声层析成像(photoacoustic tomography,PAT)时,不均匀光通量分布、组织复杂的光学和声学特性以及超声探测器的非理想特性等因素会导致重建图像质量下降。本文考虑不均匀光通量、非定常声速、超声探测器的空间脉冲响应和电脉冲响应、有限角度扫描和稀疏采样等因素的影响,建立了前向成像模型。通过交替优化求解成像模型的逆问题,实现光吸收能量分布图和声速分布图的同时重建。仿真、仿体和在体实验结果表明,与反投影法、时间反演法和短滞后空间相干法相比,该方法重建图像的结构相似度和峰值信噪比可分别提高约83%、56%、22%和80%、68%、58%。由上述结果可知,对非理想成像场景采用该方法重建的图像质量有显著提高。
Abstract:Aiming at the issue of degraded image quality in photoacoustic tomography (PAT) caused by the inhomogeneous light fluence distribution, complex optical and acoustic properties of biological tissues, and non-ideal properties of ultrasonic detectors, we propose a comprehensive forward imaging model. The model takes into account variables such as the inhomogeneous light fluence, unsteady speed of sound, spatial and electrical impulse responses of ultrasonic transducers, limited-view scanning, and sparse sampling. The inverse problem of the imaging model is solved by alternate optimization, and images representing optical absorption and speed of sound (SoS) distributions are reconstructed simultaneously. The results indicate that the structural similarity of the reconstructed images of the proposed method can be enhanced by about 83%, 56%, and 22%, in comparison with back projection, time-reversal, and short-lag spatial coherence techniques, respectively. Additionally, the peak signal-to-noise ratio can be improved by approximately 80%, 68% and 58%, respectively. This method considerably enhances the image quality of non-ideal imaging scenarios when compared to traditional techniques.
-
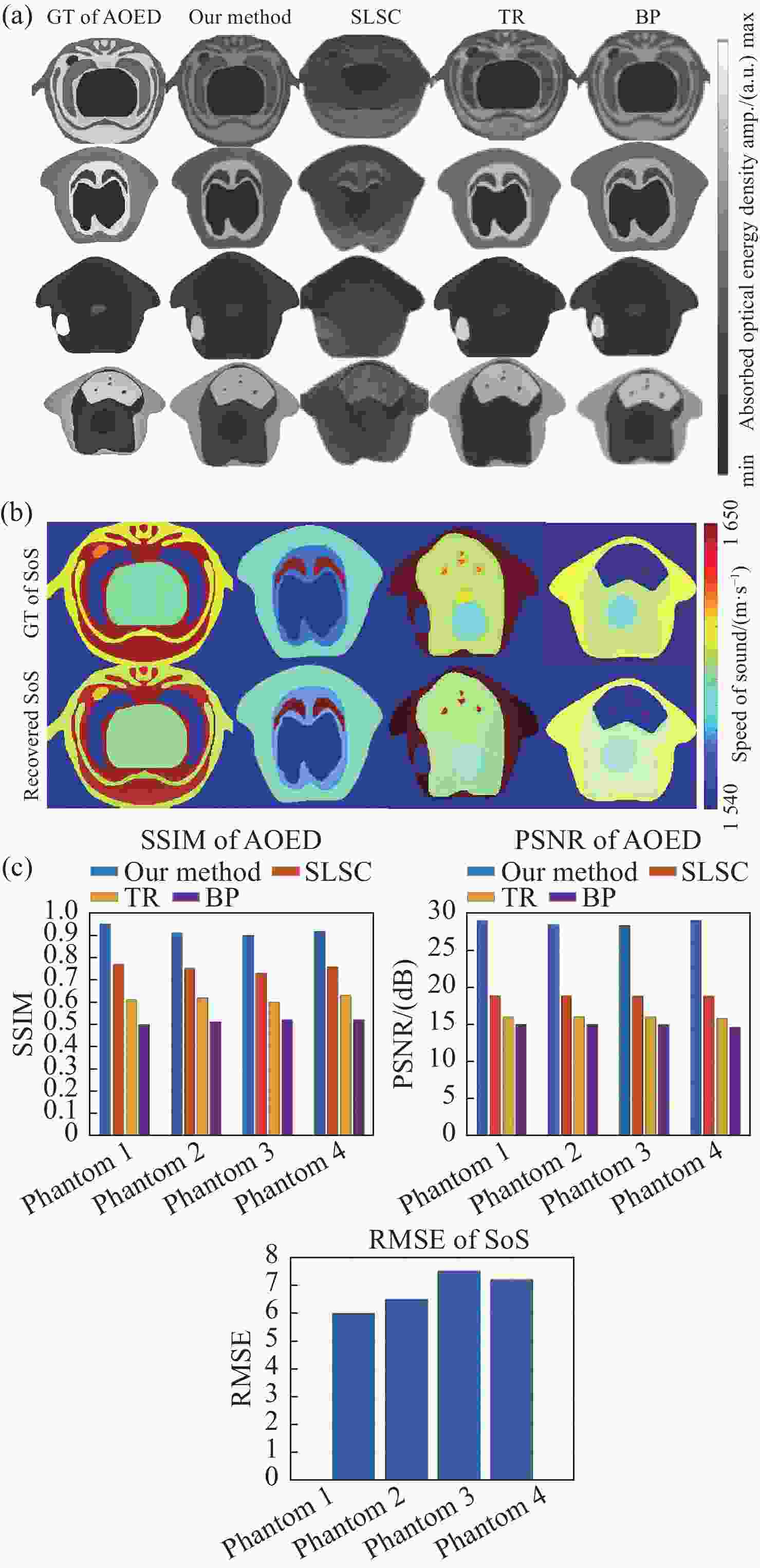
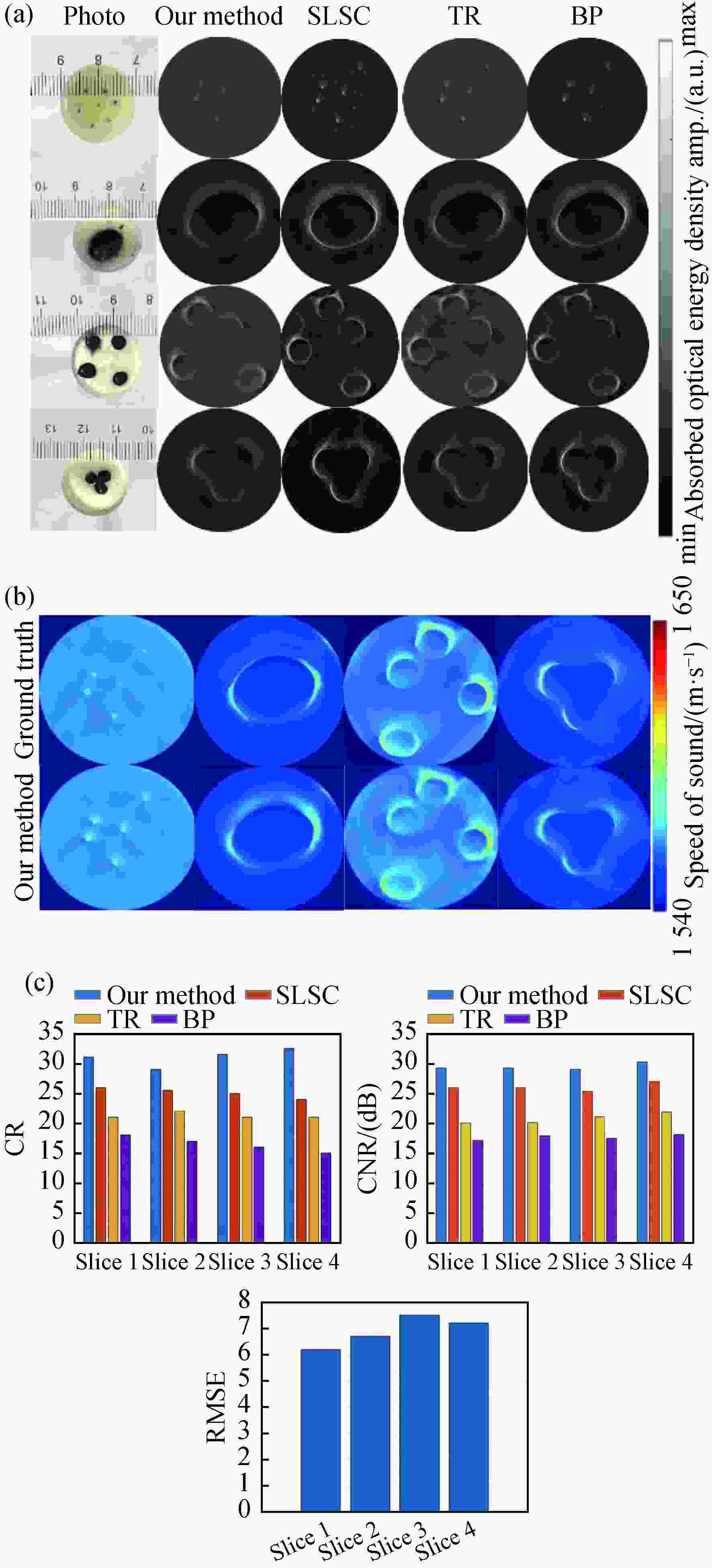
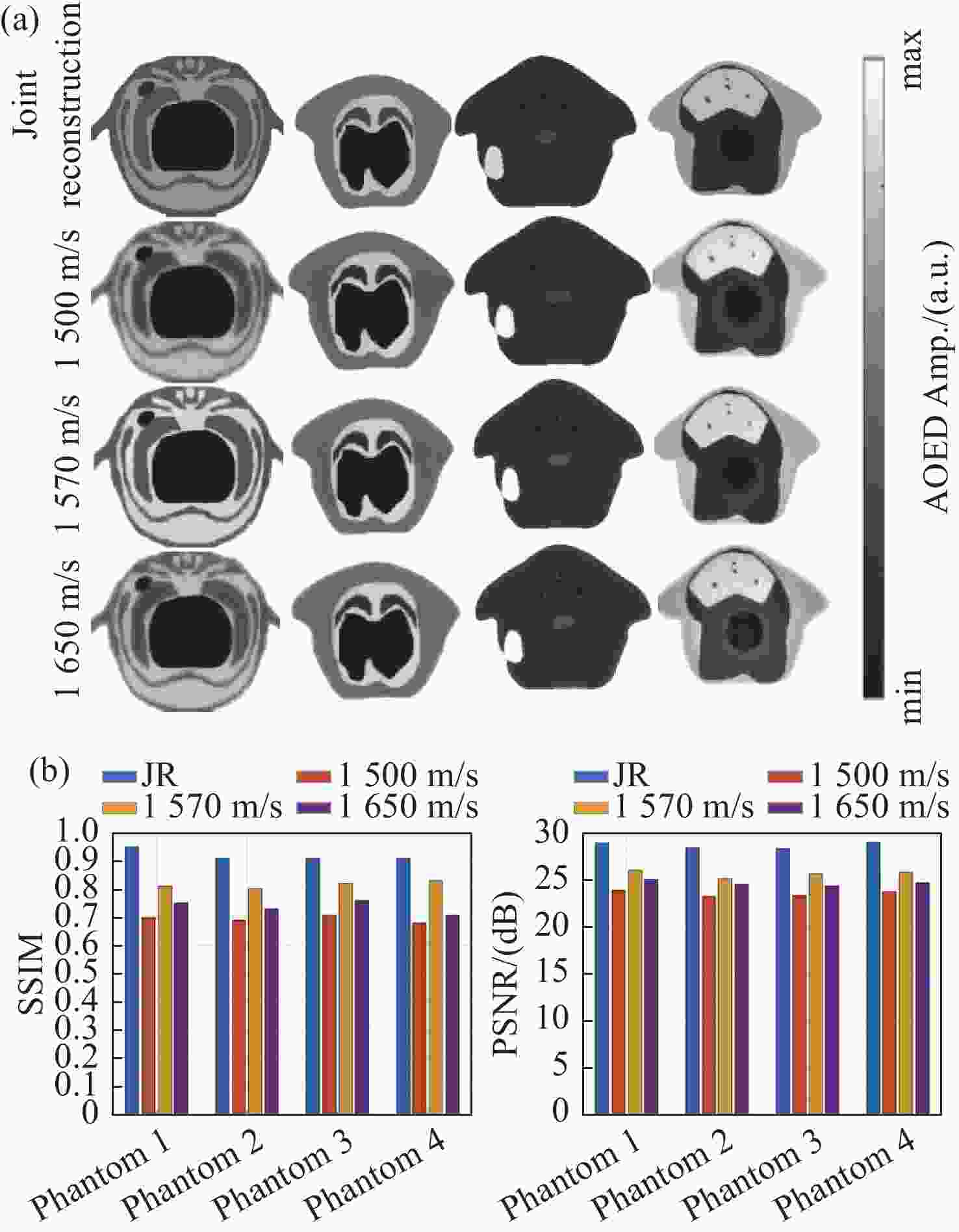
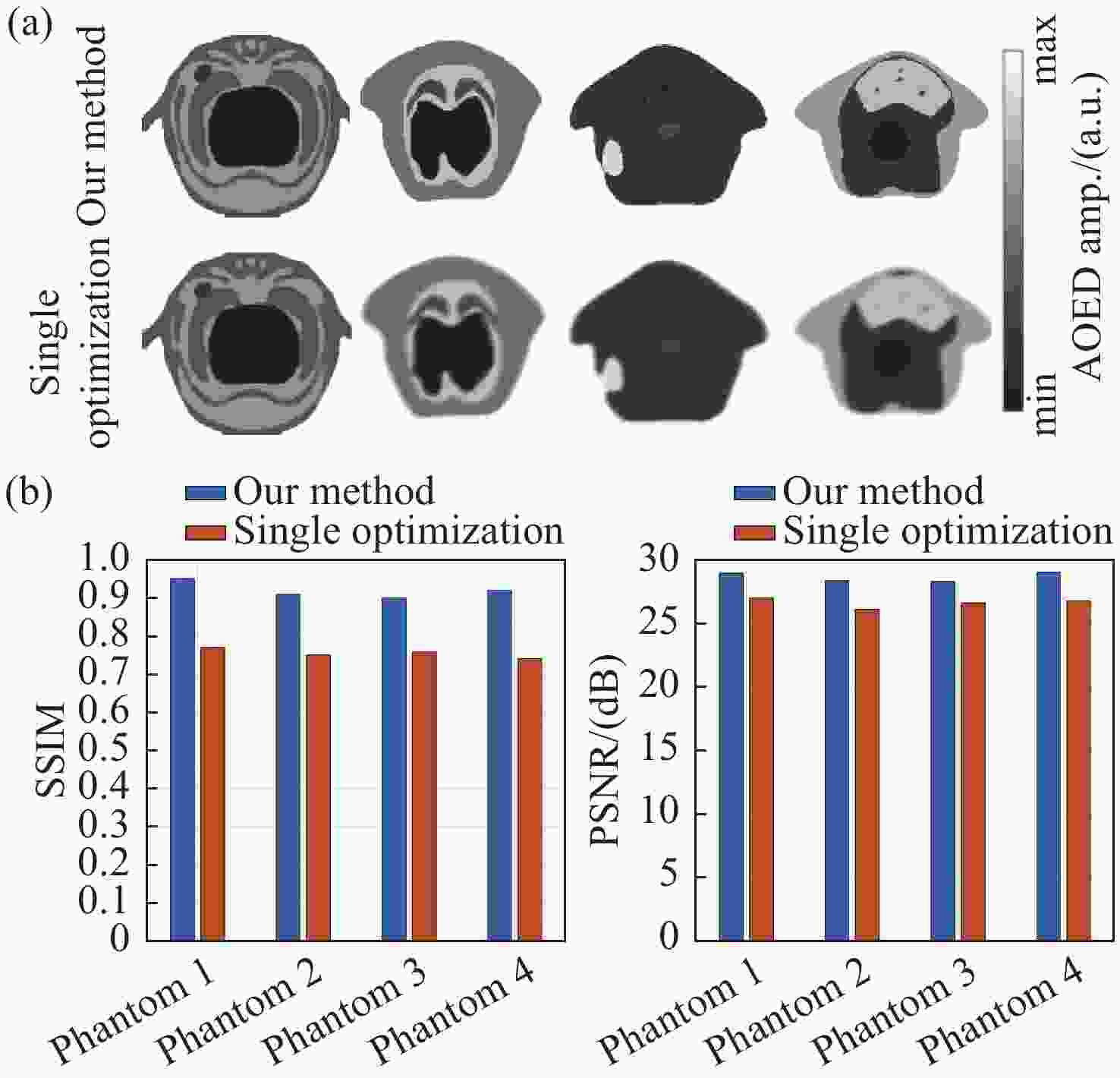
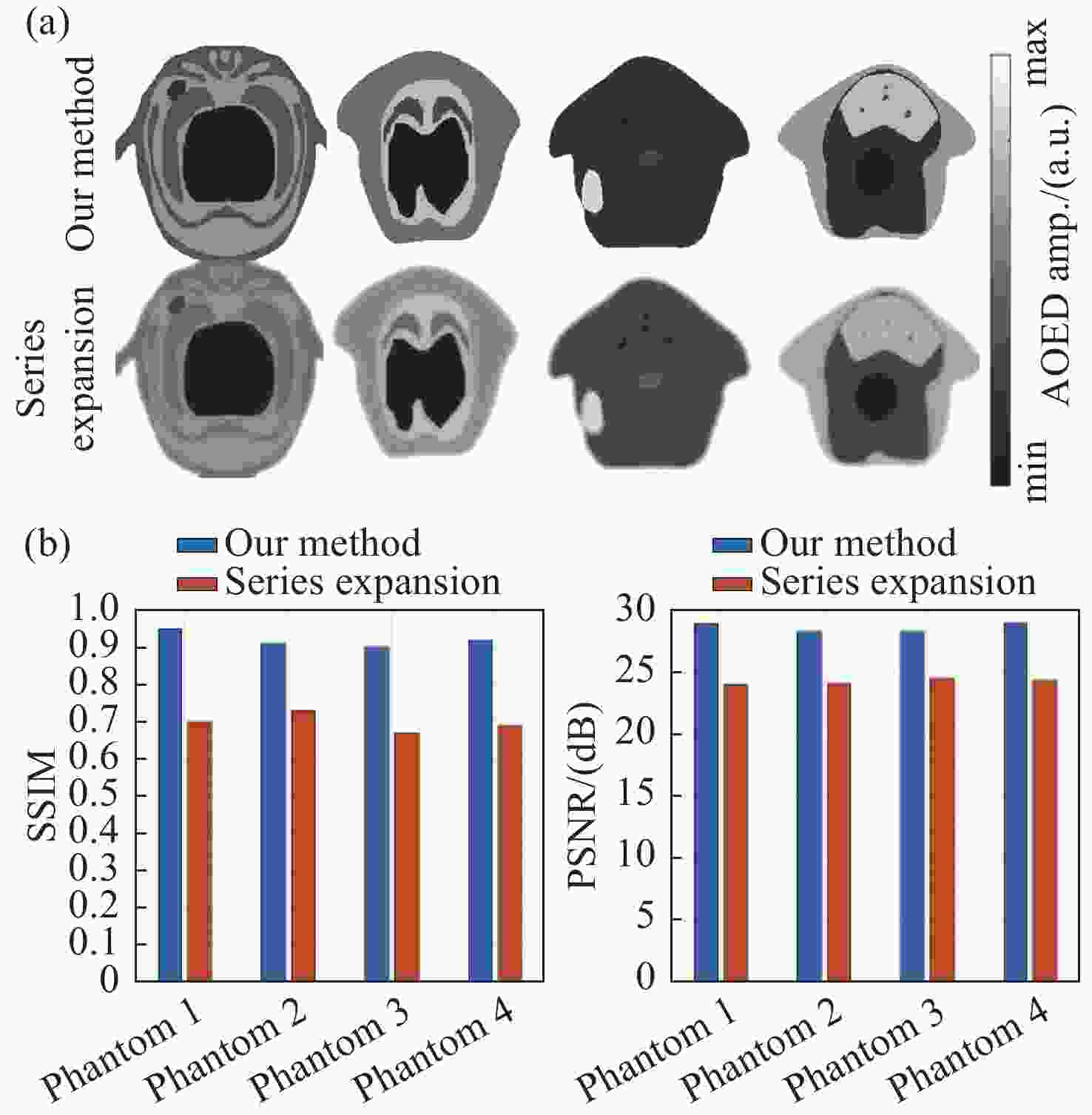
图 4 根据全角度密集采样的仿真光声信号重建的图像及其评价指标。(a)光吸收能量分布图;(b)声速分布图;(c)评价指标
Figure 4. Reconstructed distribution maps and their evaluation metrics based on simulated photoacoustic signals that are densely-sampled and collected at a full-angle. (a) AOED distribution maps; (b) SoS distribution; (c) evaluation metrics
表 1 数值仿真模型的组织特性参数
Table 1. Tissue property parameters of numerical phantoms
组织
名称组织
成分折射率 吸收系数
(cm‒1)散射系数
(cm‒1)各向异
性因子声速
(m/s)密度
(kg/L)心脏 肌肉组织 1.37 0.78 132 0.96 1580 1.060 肺 肌肉组织 1.37 0.72 114 0.95 1561 1.043 肾 结缔组织 1.36 0.76 205 0.90 1560 1.050 肝脏 肌肉组织 1.37 0.75 103 0.91 1595 1.060 胸骨 钙质 1.37 0.05 150 0.96 1580 1.050 -
[1] YAO J J, WANG L V. Recent progress in photoacoustic molecular imaging[J]. Current Opinion in Chemical Biology, 2018, 45: 104-112. doi: 10.1016/j.cbpa.2018.03.016 [2] 孙正, 王新宇. 深度学习在光声成像中的应用现状[J]. 计算机科学,2020,47(6A):148-152,156.SUN ZH, WANG X Y. Application of deep learning in photoacoustic imaging[J]. Computer Science, 2020, 47(6A): 148-152,156. (in Chinese). [3] COX B T, LAUFER J G, BEARD P C, et al. Quantitative spectroscopic photoacoustic imaging: a review[J]. Journal of Biomedical Optics, 2012, 17(6): 061202. doi: 10.1117/1.JBO.17.6.061202 [4] JAVAHERIAN A, HOLMAN S. Direct quantitative photoacoustic tomography for realistic acoustic media[J]. Inverse Problems, 2019, 35(8): 084004. doi: 10.1088/1361-6420/ab091e [5] XU M H, WANG L V. Universal back-projection algorithm for photoacoustic computed tomography[J]. Proceedings of SPIE, 2005, 5697: 251-254. doi: 10.1117/12.589146 [6] SUN ZH, HAN D D, YUAN Y. 2-D image reconstruction of photoacoustic endoscopic imaging based on time-reversal[J]. Computers in Biology and Medicine, 2016, 76: 60-68. doi: 10.1016/j.compbiomed.2016.06.028 [7] SHAN H M, WIEDEMAN C, WANG G, et al. Simultaneous reconstruction of the initial pressure and sound speed in photoacoustic tomography using a deep-learning approach[J]. Proceedings of SPIE, 2019, 11105: 1110504. [8] LOU Y, WANG K, ORAEVSKY A A, et al. Impact of nonstationary optical illumination on image reconstruction in optoacoustic tomography[J]. Journal of the Optical Society of America A, 2016, 33(12): 2333-2347. doi: 10.1364/JOSAA.33.002333 [9] 孟琪, 孙正. 生物光声层析成像中不均匀和不稳定照明解决方法[J]. 中国光学,2021,14(2):307-319. doi: 10.37188/CO.2020-0142MENG Q, SUN ZH. Solutions to inhomogeneous and unstable illumination in biological photoacoustic tomography[J]. Chinese Optics, 2021, 14(2): 307-319. (in Chinese). doi: 10.37188/CO.2020-0142 [10] CHO M H, KANG L H, KIM J S, et al. An efficient sound speed estimation method to enhance image resolution in ultrasound imaging[J]. Ultrasonics, 2009, 49(8): 774-778. doi: 10.1016/j.ultras.2009.06.005 [11] NAPOLITANO D, CHOU C H, MCLAUGHLIN G, et al. Sound speed correction in ultrasound imaging[J]. Ultrasonics, 2006, 44 Suppl: e43-e46. [12] PETROSYAN T, THEODOROU M, BAMBER J, et al. Rapid scanning wide-field clutter elimination in epi-optoacoustic imaging using comb LOVIT[J]. Photoacoustics, 2018, 10: 20-30. doi: 10.1016/j.pacs.2018.02.001 [13] LEDIJU BELL M A, KUO N, SONG D Y, et al. Short-lag spatial coherence beamforming of photoacoustic images for enhanced visualization of prostate brachytherapy seeds[J]. Biomedical Optics Express, 2013, 4(10): 1964-1977. doi: 10.1364/BOE.4.001964 [14] NGUYEN H N Y, HUSSAIN A, STEENBERGEN W. Reflection artifact identification in photoacoustic imaging using multi-wavelength excitation[J]. Biomedical Optics Express, 2018, 9(10): 4613-4630. doi: 10.1364/BOE.9.004613 [15] 孙正, 闫向阳. 采用稀疏测量数据的有限角度光声层析成像的研究进展[J]. 声学技术,2020,39(1):1-10. doi: 10.16300/j.cnki.1000-3630.2020.01.001SUN ZH, YAN X Y. Progress of limited-view photoacoustic tomography imaging based on sparse measurement[J]. Technical Acoustics, 2020, 39(1): 1-10. (in Chinese). doi: 10.16300/j.cnki.1000-3630.2020.01.001 [16] LI C H, WANG L V. Photoacoustic tomography and sensing in biomedicine[J]. Physics in Medicine & Biology, 2009, 54(19): R59-R97. [17] HOCHULI R, POWELL S, ARRIDGE S, et al. Forward and adjoint radiance Monte Carlo models for quantitative photoacoustic imaging[J]. Proceedings of SPIE, 2015, 9323: 93231P. [18] MOHAMMADI L, BEHNAM H, TAVAKKOLI J, et al. Skull’s photoacoustic attenuation and dispersion modeling with deterministic ray-tracing: towards real-time aberration correction[J]. Sensors, 2019, 19(2): 345. doi: 10.3390/s19020345 [19] WANG K, ERMILOV S A, SU R, et al. An imaging model incorporating ultrasonic transducer properties for three-dimensional optoacoustic tomography[J]. IEEE Transactions on Medical Imaging, 2011, 30(2): 203-214. doi: 10.1109/TMI.2010.2072514 [20] LIU D C, NOCEDAL J. On the limited memory BFGS method for large scale optimization[J]. Mathematical Programming, 1989, 45(1-3): 503-528. doi: 10.1007/BF01589116 [21] BECK A, TEBOULLE M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. doi: 10.1137/080716542 [22] HIRAKAWA M, NAGAKUBO D, KANZLER B, et al. Fundamental parameters of the developing thymic epithelium in the mouse[J]. Scientific Reports, 2018, 8(1): 11095. doi: 10.1038/s41598-018-29460-0 [23] LU T, WANG Y H, LI J, et al. Full-frequency correction of spatial impulse response in back-projection scheme using space-variant filtering for optoacoustic mesoscopy[J]. Photoacoustics, 2020, 19: 100193. doi: 10.1016/j.pacs.2020.100193 [24] SHENG Q W, WANG K, MATTHEWS T P, et al. A constrained variable projection reconstruction method for photoacoustic computed tomography without accurate knowledge of transducer responses[J]. IEEE Transactions on Medical Imaging, 2015, 34(12): 2443-2458. doi: 10.1109/TMI.2015.2437356 [25] ZANGERL G, MOON S, HALTMEIER M, et al. Photoacoustic tomography with direction dependent data: an exact series reconstruction approach[J]. Inverse Problems, 2019, 35(11): 114005. doi: 10.1088/1361-6420/ab2a30 [26] LI M L, WANG L V. A study of reconstruction in photoacoustic tomography with a focused transducer[J]. Proceedings of SPIE, 2007, 6437: 64371E. [27] GAVIN H P. The Levenberg-Marquardt algorithm for nonlinear least squares curve-fitting problems[D]. Durham: Duke University, 2019: 1-19. [28] 王倩, 蔡伟伟, 陶波. 基于层析成像的激光强度分布测量方法[J]. 中国光学(中英文),2023,16(4):743-752.WANG Q, CAI W W, TAO B. Laser intensity distribution measurement method based on tomographic imaging[J]. Chinese Optics, 2023, 16(4): 743-752. (in Chinese) [29] HELOU E S, ZIBETTI M V W, HERMAN G T. Fast proximal gradient methods for nonsmooth convex optimization for tomographic image reconstruction[J]. Sensing and Imaging, 2020, 21(1): 45. doi: 10.1007/s11220-020-00309-z [30] BECK A, TEBOULLE M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems[J]. IEEE Transactions on Image Processing, 2009, 18(11): 2419-2434. doi: 10.1109/TIP.2009.2028250 -






 下载:
下载: