凹非球面的非零位干涉检测技术

张旭; 李世杰; 刘丙才; 田爱玲; 梁海锋; 蔡长龙

doi:10.37188/CO.2023-0042

凹非球面的非零位干涉检测技术

doi: 10.37188/CO.2023-0042

西安工业大学光电工程学院, 陕西西安 710021

基金项目: 陕西省科技厅资助项目（No. 2022GY-222，No. 2022GY-262）；基础科研（No. JCKY2020426B009）；“一带一路”外国专家创新人才交流项目（No. DL2022040006L）

详细信息

作者简介:
张旭（1998—），女，陕西渭南人，硕士研究生，2019年于西安工业大学获得学士学位，2021年至今于西安工业大学攻读硕士研究生，主要从事光学检测方面的研究。E-mail：zhangxu19982021@163.com

李世杰（1988—），男，四川广安人，博士，副教授，硕士生导师，2014年于中国科学院光电技术研究所获得博士学位，主要从事先进光学制造技术及先进光学系统研发等方面的研究。E-mail：lishijie@xatu.edu.cn

中图分类号: TN74
计量
- 文章访问数: 196
- HTML全文浏览量: 88
- PDF下载量: 157
- 被引次数: 0
出版历程
- 收稿日期: 2023-03-13
- 修回日期: 2023-04-14
- 网络出版日期: 2023-09-26

A non-null interferometry for concave aspheric surface

School of Opto-Electronical Engineering, Xi’an Technological University, Xi’an 710021, China

Funds: Supported by Department of Science and Technology Project of Shaanxi Province (No. 2022GY-222, No. 2022GY-262); Basic Scientific Research (No. JCKY2020426B009)；"The Belt and Road" Foreign Experts Innovative Talent Exchange Project (No. DL2022040006L)

More Information

Corresponding author: lishijie@xatu.edu.cn

摘要

摘要:
为了实现凹非球面的快速、高精度与通用化检测，文中提出了一种将非球面当做球面，直接采用干涉仪检测的非零位干涉检测方法，并结合相应的数据处理方法，获得非球面的面形误差检测结果。首先，介绍了该方法的检测原理，建立了回程误差、调整误差的计算与去除模型，研究了面形误差的数据处理方法。然后，以两个不同非球面度的凹非球面为例，对其回程误差和调整误差进行了仿真计算，验证了该方法的有效性。最后，搭建了凹非球面的非零位检测实验装置，成功测量得到其面形误差。通过与自准直零位检测法或LUPHOScan轮廓测量法检测结果对比发现，两种方法测量得到的面形分布和评价指标具有高度一致性，验证了该检测方法的正确性。该检测方法在保证高精度测量的同时兼备一定的通用性与便捷性，为凹非球面的通用化检测提供了一种有效手段。
- 非球面面形测量 /
- 非零位干涉检测 /
- 回程误差 /
- 数据处理
Abstract:
To realize the rapid, high-precision, and universal testing of concave aspheric surface, a non-null interferometry method is proposed in this paper, which takes the asphere as a spherical surface and measures it directly with an interferometer. Combined with the corresponding data processing methods, the test results of the aspheric surface are obtained. Firstly, the detection theory of this method is introduced, the calculation and removal models of retrace error and adjustment error are established, and the data processing method of shape error is studied. Secondly, taking two concave aspherical surfaces with different parameters as an example, the retrace error and adjustment error are simulated, which verified the effectiveness of the method. Finally, a non-null interferometry experimental setup of concave aspheric surface is performed, and its shape error is successfully obtained. By comparing the results with autocollimation method or LUPHOScan method, it is shown that the surface distribution and evaluation indicators of the results are highly consistent, which verifies the correctness of this method. This method provides an effective measurement method for concave aspheric surface with high precision, universality, and convenience.
- aspheric surface shape measurement /
- non-null interferometry /
- retrace error /
- data processing

HTML全文

图 1 非零位干涉法直接检测非球面原理示意图

Figure 1. Schematic diagram of aspheric surface directly tested by non-null interferometry

下载: 全尺寸图片幻灯片

图 2 非零位检测光线追迹模型

Figure 2. Ray-tracing model of non-null test

下载: 全尺寸图片幻灯片

图 3 调整误差引入的像差。（a）距离引起的离焦；（b）光轴倾斜引起的倾斜误差；（c）偏心引起的彗差

Figure 3. Aberration caused by adjustment errors. (a) Distance induced defocusing; (b) tilt error caused by optical axis tilt; (c) coma caused by optical axis offset error

下载: 全尺寸图片幻灯片

图 4 非零位检测凹非球面时（a）实验装置及非零位直接检测（b）凹抛物面和（c）凹椭球面的数据

Figure 4. (a) The experiment setup of non-null test for concave aspheric; data of (b) concave paraboloid surface and (c) concave ellipsoid surface obtained by non-null direct interferometry

下载: 全尺寸图片幻灯片

图 5 非零位检测去除调整误差与回程误差。（a）凹抛物面处理后的面形结果；（b）凹椭球面处理后的面形结果；

Figure 5. Non-null test results after removing adjustment error and retrace error. (a)Test results of concave parabolic surface; (b) test results of concave ellipsoid surface

下载: 全尺寸图片幻灯片

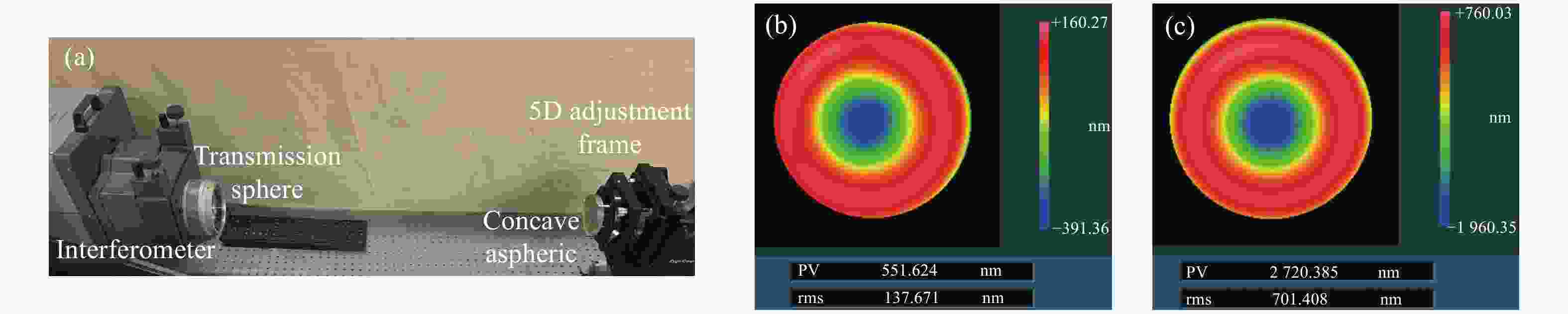
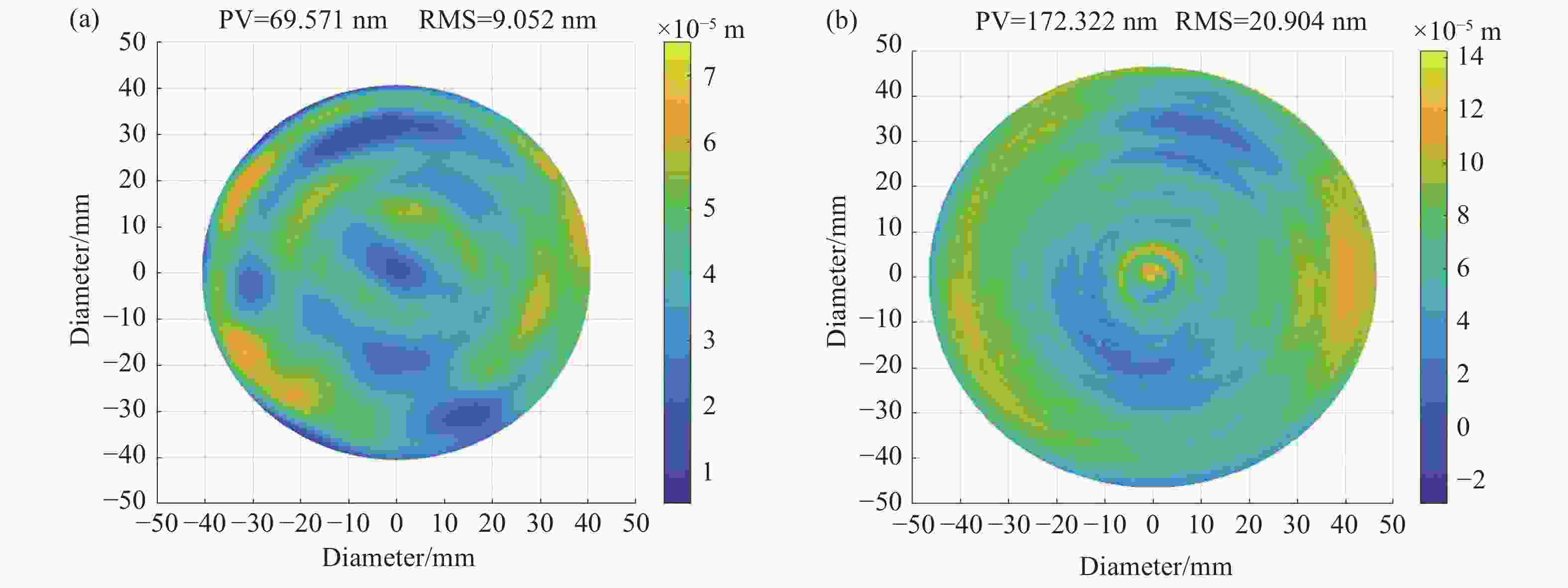
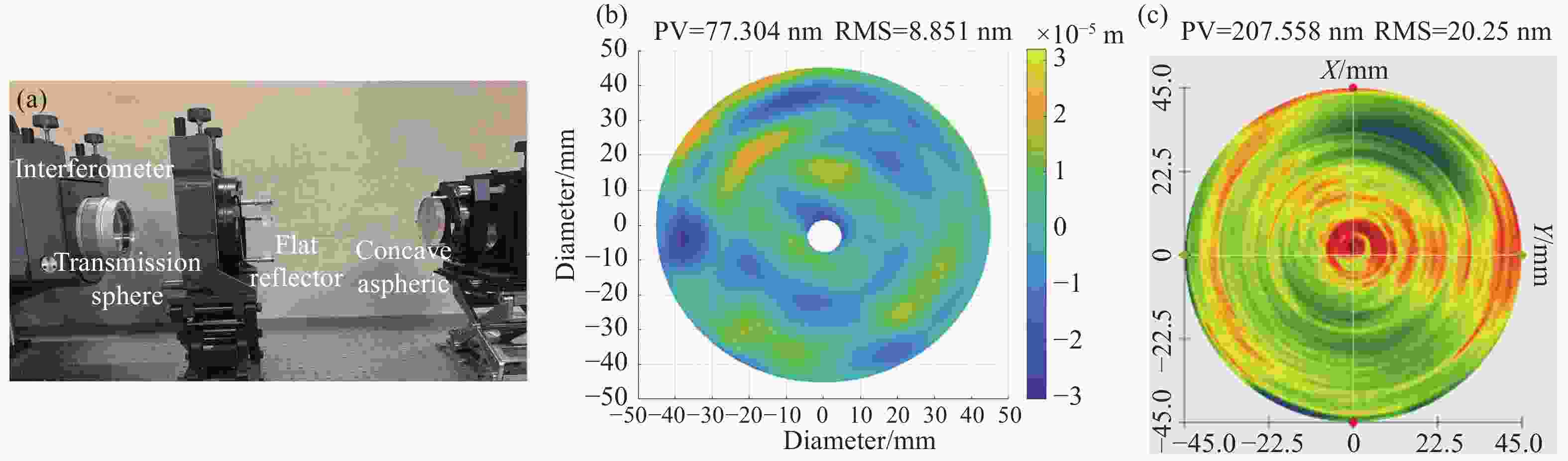
图 6 凹非球面的对比实验。(a)平面自准直法检测光路图；(b) 自准直法检测凹抛物面的数据；(c) LUPHOScan 轮廓仪测量凹椭球面的数据

Figure 6. Comparative experiment on concave aspheric. (a) The optical path diagram of plane autocollimation; (b) testing of concave paraboloid surface by autocollimation; (c) testing of concave ellipsoid surface using LUPHOScan

下载: 全尺寸图片幻灯片

表 1 Zernike多项式的项数与像差的对应关系

Table 1. Correspondence between the terms of Zernike polynomials and aberrations

Term	Polynomial	Meaning
$ {Z_4} $	$ - 1{\text{ + }}2\left( {{x^2} + {y^2}} \right) $	Power
$ {Z_7} $	$ \left( { - 2 + 3{x^2} + 3{y^2}} \right)x $	Coma X
$ {Z_8} $	$ \left( { - 2 + 3{x^2} + 3{y^2}} \right)y $	Coma Y
$ {Z_9} $	$ 1 - 6\left( {{x^2} + {y^2}} \right) + 6{\left( {{x^2} + {y^2}} \right)^2} $	Primary Spherical

下载: 导出CSV

表 2 凹抛物面参数

Table 2. Parameters of concave paraboloid surface

Parameter	Value	Parameter	Value
Aspheric type	Concave paraboloid	Maximum sag/mm	1.67
Diameter/mm	90	Maximum slope/(°)	4.25
Radius curvature of the vertex/mm	606	Maximum asphericity/μm	0.575
Conic coefficient K	−1	Best radius of the reference sphere/mm	606.835

下载: 导出CSV

表 3 凹椭球面参数

Table 3. Parameters of concave ellipsoid surface

Parameter	Value	Parameter	Value
Aspheric type	Concave ellipsoid	Maximum sag/mm	2.91
Diameter/mm	90	Maximum slope/(°)	7.39
Radius curvature of the vertex/mm	348	Maximum asphericity/μm	2.0154
Conic coefficient K	−0.66	Best radius of the reference sphere/mm	348.9615

下载: 导出CSV

表 4 凹抛物面回程误差的仿真计算结果

Table 4. Simulation calculation results of retrace error of concave paraboloid surface

OA/mm	$ O P D $	Power item $ Z_{{\mathrm{OPD}}(4)} $	Primary spherical $Z_{\Delta{{\mathrm{OPD}}(9)}}$	Retrace error
605
606
606.835
607
608

下载: 导出CSV

表 5 凹椭球面回程误差的仿真计算结果

Table 5. Simulation calculation results of retrace error of concave ellipsoid surface

OA/mm	$ O P D $	Power item $ Z_{{\mathrm{OPD}}(4)} $	Primary spherical $ Z_{\Delta{{\mathrm{OPD}}(9)}}$	Retrace error
347
348
348.9615
349
350

下载: 导出CSV

表 6 实验中距离误差引入的离焦误差与去除

Table 6. Defocusing error introduced by distance errors in experiments and its removal (nm)

Detection result	Power is adjusted to a minimum	Adjust the distance L₁	Adjust the distance L₂	Adjust the distance L₃
Fringe pattern
Surface error before removing Power	PV=639.7608 RMS=135.4192	PV=4283.4232 RMS=1200.4216	PV=1833.8544 RMS=515.732	PV=1999.0152 RMS=523.3256
Surface error after removing Power	PV= 627.1048 RMS=135.4192	PV= 654.3152 RMS=133.5208	PV=721.392 RMS=132.888	PV=656.2136 RMS=137.3176

下载: 导出CSV

表 7 实验中光轴倾斜/偏心误差引入的彗差与去除

Table 7. Comet error introduced by optical axis tilt/offset error in experiment and its removal (nm)

Detection result	Coma is adjusted to a minimum	Adjust the eccentric θ₁	Adjust the eccentric θ₂	Adjust the eccentric θ₃
Fringe pattern
Surface error before removing Coma	PV=722.6576 RMS=137.3176	PV=656.8464 RMS=133.5208	PV=641.6592 RMS=134.7864	PV=649.2528 RMS=136.6848
Surface error after removing Coma	PV= 510.6696 RMS=125.2944	PV= 489.7872 RMS=123.3960	PV= 491.0528 RMS=125.2944	PV= 488.5216 RMS=126.5600

下载: 导出CSV

参考文献(21)

[1]	刘锋伟, 吴永前, 陈强, 等. 大口径光学非球面镜先进制造技术概述[J]. 光电工程,2020,47(10):200203. LIU F W, WU Y Q, CHEN Q, et al. Overview of advanced manufacturing technology of large-aperture aspheric mirror[J]. Opto-Electronic Engineering, 2020, 47(10): 200203. (in Chinese)
[2]	师途, 杨甬英, 张磊, 等. 非球面光学元件的面形检测技术[J]. 中国光学,2014,7(1):26-46. SHI T, YANG Y Y, ZHANG L, et al. Surface testing methods of aspheric optical elements[J]. Chinese Optics, 2014, 7(1): 26-46. (in Chinese)
[3]	GUO H, LI X F, ZHANG X X, et al. Comparing the effects of highly aspherical lenslets versus defocus incorporated multiple segment spectacle lenses on myopia control[J]. Scientific Reports, 2023, 13(1): 3048. doi: 10.1038/s41598-023-30157-2
[4]	常军, 张正慧, 王蕊瑞. 特殊光学元件的新型子孔径拼接检测方法研究[J]. 物理学报,2011,60(3):034218. doi: 10.7498/aps.60.034218 CHANG J, ZHANG ZH H, WANG X R. A new sub-aperture stitching method of measuring special optical element[J]. Acta Physica Sinica, 2011, 60(3): 034218. (in Chinese) doi: 10.7498/aps.60.034218
[5]	范芯蕊, 刁晓飞, 吴剑威, 等. 高精度轴对称非球面反射镜轮廓测量方法(特邀)[J]. 红外与激光工程,2022,51(9):20220500. doi: 10.3788/IRLA20220500 FAN X R, DIAO X F, WU J W, et al. High-precision profile measurement method for axisymmetric aspheric mirror ( invited)[J]. Infrared and Laser Engineering, 2022, 51(9): 20220500. (in Chinese) doi: 10.3788/IRLA20220500
[6]	冯帅, 常军, 牛亚军, 等. 一种非对称双面离轴非球面反射镜检测补偿变焦光路设计方法[J]. 物理学报,2019,68(11):114201. doi: 10.7498/aps.68.20182253 FENG SH, CHANG J, NIU Y J, et al. A method of designing asymmetric double-sided off-axis aspheric mirror detection compensation zoom light path[J]. Acta Physica Sinica, 2019, 68(11): 114201. (in Chinese) doi: 10.7498/aps.68.20182253
[7]	HU P, XIONG X, ZHANG W H, et al. Accurate inner profile measurement of a high aspect ratio aspheric workpiece using a two-probe measuring system[J]. Applied Sciences, 2022, 12(13): 6628. doi: 10.3390/app12136628
[8]	苏航, 王孝坤, 程强, 等. 子孔径拼接和计算全息混合补偿检测大口径凸非球面(特邀)[J]. 红外与激光工程,2022,51(9):20220576. doi: 10.3788/IRLA20220576 SU H, WANG X K, CHENG Q, et al. Sub-aperture stiching and CGH mixed compensation for the testing of large convex asphere ( invited)[J]. Infrared and Laser Engineering, 2022, 51(9): 20220576. (in Chinese) doi: 10.3788/IRLA20220576
[9]	闫公敬, 张宪忠. 非零位凸非球面子孔径拼接检测技术研究[J]. 中国光学,2018,11(5):798-803. doi: 10.3788/co.20181105.0798 YAN G J, ZHANG X ZH. Research on non-null convex aspherical sub-aperture stitching detection technology[J]. Chinese Optics, 2018, 11(5): 798-803. (in Chinese) doi: 10.3788/co.20181105.0798
[10]	王孝坤, 王丽辉, 张学军. 干涉法实时测量浅度非球面技术[J]. 光学精密工程,2008,16(2):184-189. WANG X K, WANG L H, ZHANG X J. Testing of weak aspheric surface by real-time interferometry[J]. Optics and Precision Engineering, 2008, 16(2): 184-189. (in Chinese)
[11]	梁子健, 杨甬英, 赵宏洋, 等. 非球面光学元件面型检测技术研究进展与最新应用[J]. 中国光学,2022,15(2):161-186. doi: 10.37188/CO.2021-0143 LIANG Z J, YANG Y Y, ZHAO H Y, et al. Advances in research and applications of optical aspheric surface metrology[J]. Chinese Optics, 2022, 15(2): 161-186. (in Chinese) doi: 10.37188/CO.2021-0143
[12]	姚劲刚, 张金平, 郑列华, 等. 干涉零位补偿检验研究[J]. 光学学报,2015,35(6):0622003. doi: 10.3788/AOS201535.0622003 YAO J G, ZHANG J P, ZHENG L H, et al. Study on interference null compensator testing[J]. Acta Optica Sinica, 2015, 35(6): 0622003. (in Chinese) doi: 10.3788/AOS201535.0622003
[13]	ZHANG L, TIAN CH, LIU D, et al. Non-null annular subaperture stitching interferometry for steep aspheric measurement[J]. Applied Optics, 2014, 53(25): 5755-5762. doi: 10.1364/AO.53.005755
[14]	SHI T, LIU D, ZHOU Y H, et al. Practical retrace error correction in non-null aspheric testing: a comparison[J]. Optics Communications, 2017, 383: 378-385. doi: 10.1016/j.optcom.2016.09.034
[15]	贾文昕, 韩森, 张凌华, 等. 离轴椭圆柱面镜测量方法及调整误差分析[J]. 光学学报,2021,41(20):2012004. doi: 10.3788/AOS202141.2012004 JIA W X, HAN S, ZHANG L H, et al. Measurement method and alignment error analysis of off-axis elliptical cylindrical mirror[J]. Acta Optica Sinica, 2021, 41(20): 2012004. (in Chinese) doi: 10.3788/AOS202141.2012004
[16]	沙定国, 全书学, 朱秋东, 等. 光学非球面度的定义及其准确计算[J]. 光子学报,1995,24(1):91-94. SHA D G, QUAN SH X, ZHU Q D, et al. Definition and accurate calculation of optical asphericity[J]. Acta Photonica Sinica, 1995, 24(1): 91-94. (in Chinese)
[17]	方素平, 小森雅晴, 久保爱三, 等. 适用于精密复杂零件表面形状的干涉测量光学系统的光线追迹方法[J]. 机械工程学报,2009,45(2):170-177. doi: 10.3901/JME.2009.02.170 FANG S P, KOMORI M, KUBO A, et al. Ray tracing method for optical system of interferometry measurement used for form deviation of precise complex surface of machine parts[J]. Journal of Mechanical Engineering, 2009, 45(2): 170-177. (in Chinese) doi: 10.3901/JME.2009.02.170
[18]	周龙峰, 张昂, 张俊波, 等. 基于成像清晰度函数的非球面反射镜位置校正实验研究[J]. 物理学报,2016,65(13):139501. doi: 10.7498/aps.65.139501 ZHOU L F, ZHANG A, ZHANG J B, et al. Experimental research of alignment error correction by aspheric mirror based on the function of imaging quality[J]. Acta Physica Sinica, 2016, 65(13): 139501. (in Chinese) doi: 10.7498/aps.65.139501
[19]	程德文, 陈海龙, 王涌天, 等. 复杂光学曲面数理描述和设计方法研究[J]. 光学学报,2023,43(8):0822008. doi: 10.3788/AOS221980 CHENG D W, CHEN H L, WANG Y T, et al. Mathematical description and design methods of complex optical surfaces[J]. Acta Optica Sinica, 2023, 43(8): 0822008. (in Chinese) doi: 10.3788/AOS221980
[20]	GU W, SONG W H, WU G F, et al. Model-based multi-fringe interferometry using Zernike polynomials[J]. Optics and Lasers in Engineering, 2018, 105: 198-200. doi: 10.1016/j.optlaseng.2018.01.020
[21]	郭良贤, 卫俊杰, 唐培. Zernike圆域多项式镜面拟合仿真与精度研究[J]. 光学与光电技术,2018,16(6):56-62. GUO L X, WEI J J, TANG P. Fitting simulation and precision of mirror surface with Zernike circular polynomial[J]. Optics & Optoelectronic Technology, 2018, 16(6): 56-62. (in Chinese)