Data processing of high-order aspheric surface measurements using CMM in optical fabrication
-
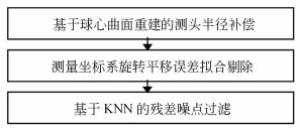
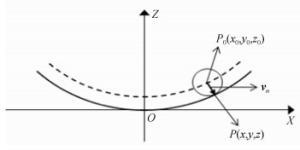
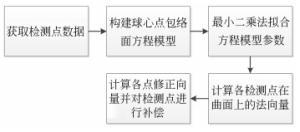
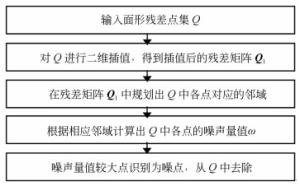
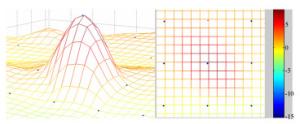
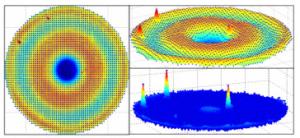
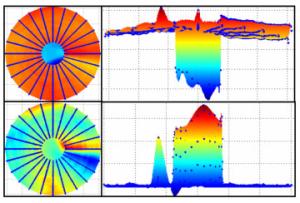
摘要: 三坐标轮廓检测是大口径高次非球面确定性加工过程中的主要面形测量手段。由于原始三坐标数据包含较大的检测误差，无法直接应用于加工过程，本文提出了一组数据处理算法对误差进行全面去除。首先，对获取的检测数据采用基于球心曲面重建的测头半径补偿算法进行测头半径误差补偿，然后对补偿后数据进行坐标系旋转平移误差去除，最后对提取的检测面形残差进行基于KNN的残差噪点过滤。其中，提出的基于球心曲面重建的测头半径补偿算法通过引入一个高精度的测头球心包络面拟合模型，来计算各检测点的测头半径补偿向量，仿真实验证明：算法补偿精度达到RMS < 4 nm；提出的基于KNN的残差噪点过滤算法，通过采用插值方法提高样本空间密度和优化噪声度量值的计算，提高了噪点的识别敏感度并实现了噪点的自动化去除。最终根据整个误差清理算法构建了检测点云处理软件，应用实践表明其有效提高了镜面加工过程中检测点云的数据处理精度和效率。Abstract: Surface measurement using a Coordinate Measuring Machine(CMM) is the main method of processing large-aperture high order aspheric mirror fabrication. Because three main types of measurement error exist in original data, the achieved surface residual cannot be directly used in mirror fabrication. Therefore, a series of algorithms for cleaning the errors of CMM point clouds is proposed. Firstly, Probe Radius Compensation(PRC) based on aspherical surface reconstruction is used to compensate for probe radius error in acquired data. Then, the compensation data is processed to remove the rotation and translation errors in the coordinate system. Finally, Surface Residual Denoising(SRD) based on KNN is used to denoise the extracted surface residual data. In the PRC algorithm, a high-precision surface fitting model for probe center points is proposed, which takes rotation and translation errors into consideration. With this model, a correcting vector for each point can be calculated to compensate for the probe radius error. The Simulation experiments show that with PRC algorithm, the precision can reach RMS < 4 nm. By densifying the sampling points with spatial interpolation and optimizing the noise characterization, the proposed SRD algorithm can identify the noise points with a high degree of sensitivity, making the denoising intelligent. Software was constructed according to the error cleaning algorithm and its application shows that it can effectively improve the accuracy and efficiency of CMM point cloud processing during aspheric mirror fabrication.
-
图 2 测量坐标系与理论面坐标系的偏差示意图
Figure 2. Sketch of deviation between measuring coordinate system and theoretical coordinate system
图 5 基于球心曲面重建的测头半径补偿算法流程
Figure 5. Flow chart of probe radius compensation based on aspherical surface reconstruction
图 6 实测数据模型拟合的残差面形分布图(单位:mm)。左图为XOY视图，右图为XOZ视图，RMS为0.12 mm
Figure 6. The residual map of model fitting with CMM data (unit mm). The left is XOY view and the right is XOZ view, RMS=0.12 mm
图 7 检测坐标系(X0, Y0, Z0)与方程理想坐标系(X, Y, Z)的空间旋转平移误差示意图
Figure 7. Sketch of the rotation and translation deviation between measuring coordinate system(X0, Y0, Z0) and theoretical coordinate system(X, Y, Z)
图 8 Matlab构建模拟验证数据流程图
Figure 8. Flow chart of constructing simulated validation data by Matlab
图 9 模拟数据模型拟合残差面形分布图(单位:mm)。RMS=1.056 2×10-6nm，PV=6.647 6×10-6 nm
Figure 9. The residual map of model fitting with simulated data(Unit mm). RMS=1.056 2×10-6 nm, PV=6.647 6×10-6 nm
图 11 插值示意图(圈为三坐标点，网格点为插值点)
Figure 11. Schematic diagram of interpolation effect(A circle represents a CMM point, the grid is represented as interpolation)
图 12 某噪点邻域的插值轮廓图(左侧为三维图，右侧为平面图)
Figure 12. Interpolation contour maps of a noise point neighborhood, the left is 3D graph and the right is plane graph
图 13 Q1平面图(左)，Q1三维图(右上)，ω分布图(右下)
Figure 13. The plane graph of Q1(left), the 3D graph of Q1(right upper), the map of ω(lower right)
图 14 Q2平面图(左上)，Q2剖面图(右上)，Q2去噪后平面图(左下)，Q2的ω剖面图(右下)
Figure 14. The plane graph of Q2(upper left), the profile of Q2(upper right), the plane graph after Q2 denoising(lower left), the map of ω(lower right)
表 1 用模拟数据拟合的测头球心曲面模型参数结果
Table 1. Parameters of spherical surface of probe center points fitted with simulated data
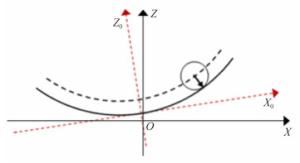
Arguments of the model Actual values Initial values given for calculation Values obtained by the model C 2 996 2 996.012 k -0.98 -0.981 271 a4 0 6.988 2×10-13 a6 0 1.013 2×10-19 pst 0 23.988 α 0.17 0 0.170 001 6 β -0.01 0 -0.009 999 9 Δx 0.8 0 0.796 523 4 Δy 4 0 -4.059 332 1 
下载: 导出CSV
表 2 补偿算法的坐标补偿精度(单位mm)
Table 2. Precision of the PRC algorithm(Unit mm)
Coordinate error Root mean square Peak-Valley of error diff-X 4.083×10-6 2.013×10-5 diff-Y 4.058×10-6 2.104×10-5 diff-Z 5.046×10-7 2.021×10-6
下载: 导出CSV
表 3 Leiz三坐标与本文算法补偿结果对比(单位mm)
Table 3. Result comparison of Leiz CMM algorithm and the PRC (Unit mm)
Coordinate error Root mean square Peak-Valley of error diff-X 7.724×10-6 8.316×10-5 diff-Y 1.008×10-5 1.014×10-4 diff-Z 2.161×10-6 8.832×10-6
下载: 导出CSV
表 4 空间五维误差仿真检测数据
Table 4. Simulation CMM data of spatial 5D-errors
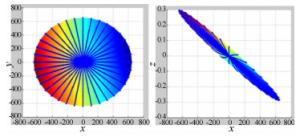
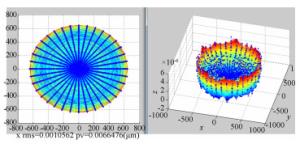
理论轮廓 五维误差 残差面形 实验数据一 D=600 mm α=0.006 3° 面形=低频像散 C=-1/1 646.4 β=0.003 5° pv=2.678 μm k=-0.986 1 Δx=0.129 1 mm rms=0.549 μm a4=4×10-16 Δy=0.153 2 mm a6=0 Δz=-61.37 mm 
实验数据二 D=1 000 mm α=-2.341° 面形=中高频加工痕迹 C=1/208 5 β=-0.531 5° pv= 3.057 μm k=-0.97 Δx=4.296 mm rms=0.342 μm a4=3×10-19 Δy=3.372 mm a6=-2×10-23 Δz=-50.37 mm 
下载: 导出CSV
表 5 实验数据一/二的空间五维误差拟合精度
Table 5. Fitting precision of spatial 5D-error test data 1 and data 2
Test data 1 Test data 2 diff-α -4.131×10-7° 0.058 75° diff-β 4.625×10-7° 0.010 62° diff-Δx -0.003 6 mm 0.043 1 mm diff-Δy -0.006 9 mm 0.171 3 mm diff-Δz 1.16×10-4 mm 1.33×10-4 mm
下载: 导出CSV
-
[1] 薛栋林, 郑立功, 张峰.基于光学自由曲面的离轴三反光学系统[J].光学 精密工程, 2011, 19(12):2813-2820. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201112001XUE D L, ZHENG L G, ZHANG F. Off-axis three-mirror system based on freeform mirror[J]. Opt. Precision Eng., 2011, 19(12):2813-2820. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201112001 [2] 李欢, 周峰.成像光谱仪宽视场离轴三反望远系统的光学设计[J].航天返回与遥感, 2012, 33(2):28-33. doi: 10.3969/j.issn.1009-8518.2012.02.006LI H, ZHOU F. Optical design of wide-field off-axis three-mirror telescope systems[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(2):28-33. (in Chinese) doi: 10.3969/j.issn.1009-8518.2012.02.006 [3] 刘兆军, 周峰, 胡斌, 等.长焦距同轴三反空间相机光学系统研究[J].航天返回与遥感, 2011, 32(6):46-52. doi: 10.3969/j.issn.1009-8518.2011.06.009LIU ZH J, ZHOU F, HU B, et al.. Study on coaxis three-mirror-anastigmat space camera with long focal length[J]. Spacecraft Recovery & Remote Sensing, 2011, 32(6):46-52. (in Chinese) doi: 10.3969/j.issn.1009-8518.2011.06.009 [4] 孟晓辉, 王永刚, 马仙梅, 等.空间同轴三反相机φ520mm次镜的加工与检测[J].红外与激光工程, 2017, 46(8):0818002. http://d.old.wanfangdata.com.cn/Periodical/hwyjggc201708024MENG X H, WANG Y G, MA X M, et al.. Fabrication and test for φ520 mm secondary mirror of on-axis three mirror space camera[J]. Infrared and Laser Engineering, 2017, 46(8):0818002. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/hwyjggc201708024 [5] 孟晓辉, 王永刚, 李文卿, 等. φ420 mm高次非球面透镜的加工与检测[J].光学 精密工程, 2016, 24(12):3068-3075. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201612027MENG X H, WANG Y G, LI W Q, et al.. Fabricating and testing of φ520 mm high-order aspheric lens[J]. Opt. Precision Eng., 2016, 24(12):3068-3075. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201612027 [6] 韩哈斯额尔敦, 曾志革, 刘海涛, 等.光学加工机器人定位误差测量与分析[J].光电工程, 2017, 44(5):516-522. doi: 10.3969/j.issn.1003-501X.2017.05.007HASIRDEN, ZENG ZH G, LIU H T, et al.. Measurement and analyses on positioning accuracy for optical processing robots[J]. Opto-Electronic Engineering, 2017, 44(5):516-522. (in Chinese) doi: 10.3969/j.issn.1003-501X.2017.05.007 [7] 林长青, 景洪伟, 匡龙, 等.离轴非球面镜精磨阶段的三坐标检测技术[J].强激光与粒子束, 2012, 24(11):2665-2668. http://d.old.wanfangdata.com.cn/Periodical/qjgylzs201211031LIN CH Q, JING H W, KUANG L, et al.. Measuring technique for off-axis aspherical mirror in fine grinding process using coordinate measurement machine[J]. High Power Laser and Particle Beams, 2012, 24(11):2665-2668. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/qjgylzs201211031 [8] 范晓明, 罗词金, 徐学科, 等.光学非球面三坐标测量中的像散补偿[J].光学 精密工程, 2016, 24(12):3012-3019. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201612019FAN X M, LUO C J, XU X K, et al.. Compensation of astigmatism in coordinate measurement for optical aspheric elements[J]. Opt. Precision Eng., 2016, 24(12):3012-3019. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201612019 [9] 王建明.三坐标轮廓测量仪检测非球面研究[D].苏州: 苏州大学, 2013.WANG J M. Study on aspheric surface measurement using coordinate contour measuring machine[D]. Suzhou: Soochow University, 2013. (in Chinese) [10] LIN Y C, SUN W I. Probe radius compensated by the multi-cross product method in freeform surface measurement with touch trigger probe CMM[J]. The International Journal of Advanced Manufacturing Technology, 2003, 21(10-11):902-909. doi: 10.1007/s00170-002-1413-0 [11] 张毅, 刘旭敏, 隋颖, 等.基于K-近邻点云去噪算法的研究与改进[J].计算机应用, 2009, 29(4):1011-1014. http://d.old.wanfangdata.com.cn/Periodical/jsjyy200904029ZHANG Y, LIU X M, SUI Y, et al.. Research and improvement of denoising method based on K-neighbors[J]. Journal of Computer Applications, 2009, 29(4):1011-1014. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jsjyy200904029 [12] SHI K L, YONG J H, SUN J G, et al.. B-spline surface interpolation[J]. Computer Aided Geometric Design, 2011, 28(6):368-381. doi: 10.1016/j.cagd.2011.06.002 -
下载:
计量
- 文章访问数: 2319
- HTML全文浏览量: 1056
- PDF下载量: 165
- 被引次数: 0
