快速反射镜在像移补偿中的应用

王正玺; 张葆; 李贤涛; 张士涛

doi:10.3788/CO.20201301.0095

快速反射镜在像移补偿中的应用

doi: 10.3788/CO.20201301.0095

王正玺^{1, 2,},
张葆^1, ,,
李贤涛¹,
张士涛^{1, 2}

1.
中国科学院长春光学精密机械与物理研究所, 吉林长春 130033
2.
中国科学院大学, 北京 100049

基金项目:

国家自然科学基金 1705225

详细信息

作者简介:
王正玺(1989-), 男, 河北保定人, 博士研究生, 2014年于哈尔滨工业大学获得学士学位, 主要从事光电平台视轴稳定控制技术研究。E-mail:ldh_wh@163.com

张葆(1966-), 男, 吉林磐石人, 研究员, 博士生导师, 1989年、1994年于长春光机学院分别获得学士、硕士学位, 2004年于中国科学院长春光学精密机械与物理研究所获得博士学位, 主要从事航空光电成像技术方面的研究。E-mail:clearsky_zh@163.com

中图分类号: TP273
计量
- 文章访问数: 1780
- HTML全文浏览量: 742
- PDF下载量: 114
- 被引次数: 0
出版历程
- 收稿日期: 2019-03-19
- 修回日期: 2019-05-14
- 刊出日期: 2020-02-01

Application of fast steering mirror in image motion compensation

WANG Zheng-xi^{1, 2
,},
ZHANG Bao^{1
, ,},
LI Xian-tao¹,
ZHANG Shi-tao^{1, 2}

1.
Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033
2.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds:

National Natural Science Foundation of China 1705225

More Information

Corresponding author: ZHANG Bao, E-mail:clearsky_zh@163.com

摘要

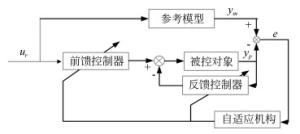
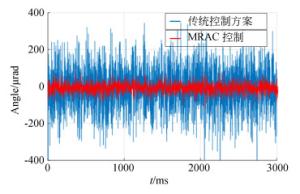
摘要: 本文提出了一种基于快速反射镜的像移补偿方法用于解决航空成像中的像移问题。首先通过计算航空相机在曝光时间内的像移速度证明了像移补偿的必要性；针对快速反射镜存在伺服模型不确定性的问题，设计了模型参考自适应控制器；最后通过实验验证了该算法的性能，结果显示：采用本算法后，快速反射镜的阶跃响应稳定时间降低了50%以上，在振动情况下快速反射镜的稳定精度都可以达到10 μrad，精度比传统控制方案提升10倍以上。最终的像移补偿成像实验成功验证了基于快速反射镜的像移补偿方案有较高的工程应用价值。
- 快速反射镜 /
- 像移补偿 /
- 像移速度 /
- 模型参考自适应控制
Abstract: A method of image motion compensation based on Fast Steering Mirrors (FSM) is proposed to solve the problem of image motion in aeronautical imaging. Firstly, the necessity of image motion compensation is proven by calculating the image motion velocity of the aeronautical camera in exposure time. Then, a model reference adaptive controller is designed to solve uncertainties in the servo model of an FSM. The experimental results indicate that the stable time of step response is reduced by more than 50% comparing with traditional methods. The stability accuracy of the FSM can reach 10 μrad even under vibration condition, which means the accuracy of this method is 10 times better than that of traditional methods. A final image motion compensation imaging experiment proves that our image motion compensation scheme based on an FSM has high value in engineering applications.
- Fast Steering Mirrors(FSM) /
- image motion compensation /
- image motion velocity /
- model reference adaptive controller

HTML全文

图 1 航空成像系统几何关系图

Figure 1. Geometry diagram of aeronautical imaging system

下载: 全尺寸图片幻灯片

图 2 MRAC控制系统结构框图

Figure 2. Block diagram of MRAC

下载: 全尺寸图片幻灯片

图 3 用状态方程描述的MRAC系统框图

Figure 3. MRAC system block diagram described by equation of state

下载: 全尺寸图片幻灯片

图 4 快速反射镜结构示意图

Figure 4. Schematic diagram of a FSM

下载: 全尺寸图片幻灯片

图 5 快速反射镜频率响应

Figure 5. Frequency responses of the FSM system

下载: 全尺寸图片幻灯片

图 6 带速率反馈的二阶系统示意图

Figure 6. Block diagram of a second order system with rate feedback

下载: 全尺寸图片幻灯片

图 7 引入速率反馈前后快速反射镜开环频率响应

Figure 7. Open loop frequency responses of the FSM with and without rate feedback

下载: 全尺寸图片幻灯片

图 8 ω_nt_s-ξ关系曲线

Figure 8. ω_nt_s-ξ relationship curves

下载: 全尺寸图片幻灯片

图 9 快速反射镜硬件实验平台

Figure 9. Hardware experimental platform for FSM

下载: 全尺寸图片幻灯片

图 10 快速反射镜闭环阶跃响应曲线

Figure 10. Closed-loop step response curve of FSM

下载: 全尺寸图片幻灯片

图 11 阶跃响应稳态误差

Figure 11. Steady state error of step response

下载: 全尺寸图片幻灯片

图 12 振动条件下的位置稳定误差

Figure 12. Position stability error under vibration conditions

下载: 全尺寸图片幻灯片

图 13 成像系统原理示意图

Figure 13. Schematic diagram of imaging system

下载: 全尺寸图片幻灯片

图 14 平台扫描速度为5(°)/s时，几种情况的像移补偿效果对比

Figure 14. Comparison of image shift compensation effect for three different conditons with platform scanning speed of 5(°)/s

下载: 全尺寸图片幻灯片

表 1 不同转速时系统分辨率对比

Table 1. System resolution comparison at different speeds

平台转速(°/s) 2 3 4 5

分辨率(cycles/mm) 13 13 13 12

下载: 导出CSV

参考文献(22)

[1]	李刚, 杨名宇.基于联合变换相关的机载航空相机像移测量[J].中国光学, 2015, 8(3):401-406. http://www.chineseoptics.net.cn/CN/abstract/abstract9301.shtml LI G, YANG M Y. Image motion measurement for airborne camera based on joint transform correlation[J]. Chinese Optics, 2015, 8(3):401-406. (in Chinese) http://www.chineseoptics.net.cn/CN/abstract/abstract9301.shtml
[2]	张玉欣, 刘宇, 葛文奇.像移补偿技术的发展与展望[J].中国光学与应用光学, 2010, 3(2):112-118. doi: 10.3969/j.issn.2095-1531.2010.02.003 ZHANG Y X, LIU Y, GE W Q. Development and prospect of image motion compensation technology[J]. Chinese Journal of Optics and Applied Optics, 2010, 3(2):112-118. (in Chinese) doi: 10.3969/j.issn.2095-1531.2010.02.003
[3]	张丽, 汤恩生, 许敬旺.空间相机像移补偿方法研究[J].航天返回与遥感, 2007, 28(3):19-22, 32. doi: 10.3969/j.issn.1009-8518.2007.03.004 ZHANG L, TANG E SH, XU J W. Studies on the image motion compensation methods of space camera[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(3):19-22, 32. (in Chinese) doi: 10.3969/j.issn.1009-8518.2007.03.004
[4]	陈黎, 翟林培, 李友一.基于航空遥感器像移补偿实现方法的研究[J].计算机测量与控制, 2009, 17(1):154-155, 163. http://d.old.wanfangdata.com.cn/Periodical/jsjzdclykz200901052 CHEN L, ZHAI L P, LI Y Y. Research to realize aerial remote sensor image motion compensation[J]. Computer Measurement & Control, 2009, 17(1):154-155, 163. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jsjzdclykz200901052
[5]	王德江, 董斌, 李文明, 等. TDI CCD电荷转移对遥感相机成像质量的影响[J].光学精密工程, 2011, 19(10):2500-2506. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201110027 WANG D J, DONG B, LI W M, et al.. Influence of TDI CCD charge transfer on imaging quality in remote sensing system[J]. Opt. Precision Eng., 2011, 19(10):2500-2506. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201110027
[6]	NOUGUÈS P O, BAIZE P, ROLAND F, et al.. Third-generation naval IRST using the step-and-stare architecture[J]. Proceedings of SPIE, 2008, 6940:69401B. doi: 10.1117-12.773953/
[7]	AMON M, STOKES B. Stabilized step/stare scanning device:US, 5663825[P]. 1997-09-02.
[8]	HELD K J, ROBINSON B H. TIER Ⅱ Plus airborne EO sensor LOS control and image geolocation[C]. Proceedings of 1997 IEEE Aerospace Conference, IEEE, 1997.
[9]	李永昌, 金龙旭, 李国宁, 等.宽视场遥感相机像移速度模型及补偿策略[J].武汉大学学报(信息科学版), 2018, 43(8):1278-1286. http://d.old.wanfangdata.com.cn/Periodical/whchkjdxxb201808022 LI Y CH, JIN L X, LI G N, et al.. Image motion velocity model and compensation strategy of wide-field remote sensing camera[J]. Geomatics and Information Science of Wuhan University, 2018, 43(8):1278-1286. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/whchkjdxxb201808022
[10]	路朋罗, 李永昌, 金龙旭, 等.大视场空间相机的像移速度场模型及卫星三轴姿态稳定度分析[J].光学精密工程, 2016, 24(9):2173-2182. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201609011 LU P L, LI Y CH, JIN L X, et al.. Image motion velocity field model of space camera with large field and analysis on three-axis attitude stability of satellite[J]. Opt. Precision Eng., 2016, 24(9):2173-2182. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201609011
[11]	DEY N, MONDAL U, MONDAL D. Design of a H-infinity robust controller for a DC servo motor system[C]. Proceedings of 2016 International Conference on Intelligent Control Power and Instrumentation, IEEE, 2016.
[12]	RHOUMA T, KELLER J Y, SAUTER D, et al. Active GLR detector for resilient LQG controller in networked control systems[J]. IFAC-Papers OnLine, 2015, 48(21):754-759. doi: 10.1016/j.ifacol.2015.09.617
[13]	张怡, 刘向杰.互联电力系统鲁棒分布式模型预测负荷频率控制[J].控制理论与应用, 2016, 33(5):621-630. http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201605008 ZHANG Y, LIU X J. Robust distributed model predictive control for load frequency control of uncertain power systems[J]. Control Theory & Applications, 2016, 33(5):621-630. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201605008
[14]	NGUYEN N, KRISHNAKUMAR K, BOSKOVIC J. An optimal control modification to model-reference adaptive control for fast adaptation[C]. AIAA Guidance, Navigation and Control Conference and Exhibit, AIAA, 2013: 705-741.
[15]	黄元峰, 石云宝, 庞绍平, 等. MRAC-PID复合控制在液力控制系统中的应用[J].吉林工业大学自然科学学报, 2000, 30(4):70-74. doi: 10.3969/j.issn.1671-5497.2000.04.019 HUANG Y F, SHI Y B, PANG SH P, et al.. Study on MRAC-PID control method and application in hydrodynamic control system[J]. Natural Science Journal of Jilin University of Technology, 2000, 30(4):70-74. (in Chinese) doi: 10.3969/j.issn.1671-5497.2000.04.019
[16]	KAMNIK R, MATKO D, BAJD T. Application of model reference adaptive control to industrial robot impedance control[J]. Journal of Intelligent and Robotic Systems, 1998, 22(2):153-163. doi: 10.1023/A:1007932701318
[17]	WU G Q, WU SH N, BAI Y G, et al.. Experimental studies on model reference adaptive control with integral action employing a rotary encoder and tachometer sensors[J]. Sensors, 2013, 13(4):4742-4759. doi: 10.3390/s130404742
[18]	BÖHM M, DEMETRIOU M A, REICH S, et al.. Model reference adaptive control of distributed parameter systems[J]. SIAM Journal on Control and Optimization, 1998, 36(1):33-81. http://d.old.wanfangdata.com.cn/Periodical/xtkxysx201306006
[19]	HAFEZ M, SIDLER T C, SALATHÉ R P, et al.. Design, simulations and experimental investigations of a compact single mirror tip/tilt laser scanner[J]. Mechatronics, 2000, 10(7):741-760. doi: 10.1016/S0957-4158(99)00093-8
[20]	SWEENEY M N, RYNKOWSKI G A, KETABCHI M, et al.. Design considerations for fast-steering mirrors (FSMs)[J]. Proceedings of SPIE, 2002, 4773:63-73. doi: 10.1117/12.469197
[21]	李贤涛, 张晓沛, 毛大鹏, 等.高精度音圈快速反射镜的自适应鲁棒控制[J].光学精密工程, 2017, 25(9):2428-2436. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201709021 LI X T, ZHANG X P, MAO D P, et al.. Adaptive robust control over high-performance VCM-FSM[J]. Opt. Precision Eng., 2017, 25(9):2428-2436. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201709021
[22]	赵磊, 纪明, 王明歆, 等.快速反射镜驱动形式对伺服带宽的影响[J].光学精密工程, 2019, 27(2):393-401. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201902015 ZHAO L, JI M, WANG M M, et al.. Influence of driving forms on servo bandwidth[J]. Opt. Precision Eng., 2019, 27(2):393-401. (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201902015