Electron wave packet interference images in above-threshold ionization of hydrogen atoms by few-cycle intense laser fields
-
摘要: 采用电子波包干涉方法研究了长程库仑势以及再散射电子对氢原子在少周期强激光场中阈上电离的影响。首先，利用强场近似及Coulomb-Volkov近似结合时间窗函数，模拟了氢原子在波长为800 nm且脉宽为5 fs的线性极化激光场中单电离的周期内干涉及周期间干涉图像，发现在长程库仑势作用下周期内干涉及周期间干涉共同作用形成了二维动量谱中的部分扇形结构条纹，其余部分扇形条纹的形成与再散射电子有关。然后，通过数值求解含时薛定谔方程计算了深度隧穿电离机制下氢原子的二维动量谱，在二维动量谱中出现了明显的径向条纹。研究结果表明，该径向条纹的产生与长程库仑势无关，是再散射电子波包干涉形成的。Abstract: By using electron wave packet interference methodology, the effects of long-range Coulomb potential and rescattering electrons on the above-threshold ionization of hydrogen atoms in few-cycle intense laser field are investigated. Firstly, using the strong field approximation and Coulomb-Volkov approximation combined with the time window function, the intra- and inter-cycle interference images of hydrogen atoms in a linearly polarized laser field with a wavelength of 800 nm and a pulse width of 5 fs are simulated. It was found that a part of fanlike structure in 2D momentum spectra is formed by the interplay of inter-cycle and intra-cycle interferences under the action of long-range Coulomb. Subsequently, the first principle solution of the Time-Dependent Schrodinger Equation(TDSE) is used to calculate the 2D momentum spectrum of hydrogen atoms under the deep tunneling ionization mechanism. It was found that there are some abvious radial fringes in the 2D momentum spectrum. The results show that the radial fringes are formed by the interference of the rescattering electron wave packets, which are independent of the long-range coulomb potential.
-
图 1 激光场的电场及矢势，I=4.0×1014 W/cm2, λ=800 nm, CEP=0, Γ=5 fs
Figure 1. Electric field and vector potential of laser field with I=4.0×1014 W/cm2, λ=800 nm, CEP=0, Γ=5 fs
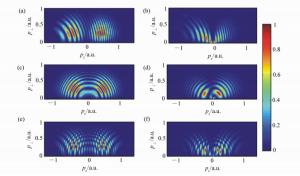
图 6 H原子TDSE二维光电子动量谱，I=4.0×1014 W/cm2，λ=800 nm，CEP=0。(a)、(c)及(e)为考虑库仑势的计算结果，(b)、(d)及(f)为考虑短程势的计算结果；(a)和(b)脉冲持续时间为2 cycles；(c)和(d)为4 cycles；(e)和(f)为8 cycles
Figure 6. TDSE 2D photoelectron momentum spectra of H atom when I=4.0×1014 W/cm2, λ=800 nm and CEP=0. (a)、(c) and (e) calculated with coulomb potential, (b)、(d) and (f) calculated without coulomb potential; (a) and (b) with 2 cycles pulse; (c) and (d) with 4 cycles pulse; (e) and (f) with 8 cycles pulse
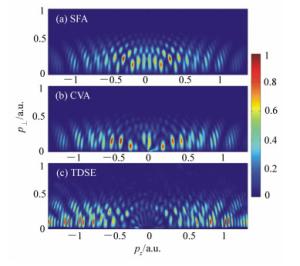
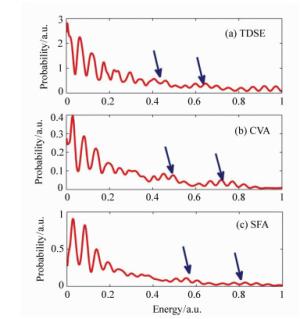
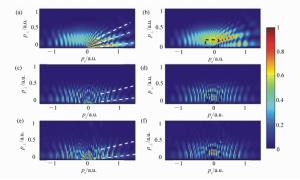
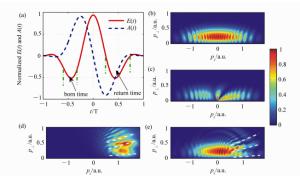
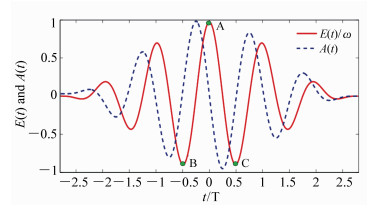
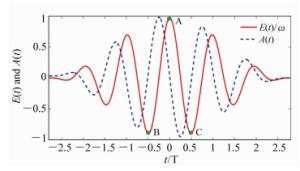
图 7 H原子二维光电子动量谱及对应的电场和矢势，激光参数与图 6(a)相同。(a)电场和矢势；(b)SFA结果；(c)CVA结果；(d)SFA2结合时间窗的结果；(e)SFA2结果
Figure 7. Electric field and vector potential, and 2D photoelectron momentum spectra of H atom under the same laser field as shown in Fig. 6(a). (a)Electric field and vector potential; (b)result from SFA; (c)result from CVA; (d)result from SFA2 with time windows; (e)result from SFA2
-
[1] LIN C D, LE A T, CHEN ZH J, et al.. Strong-field rescattering physics—self-imaging of a molecule by its own electrons[J]. Journal of Physics B:Atomic, Molecular and Optical Physics, 2010, 43(12):122001. doi: 10.1088/0953-4075/43/12/122001 [2] 仝小刚, 王国利, 周效信, 等.利用高能光电子的非对称性确定少周期激光的载波相位[J].光学学报, 2016, 36(3):0319002. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201603025TONG X G, WANG G L, ZHOU X X, et al.. Carrier phase determination for few-cycle laser pulses based on asymmetry of ionized high-energy electrons[J]. Acta Optica Sinica, 2016, 36(3):0319002.(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gxxb201603025 [3] LINDNER F, SCHÄTZEL M G, WALTHER H, et al.. Attosecond double-slit experiment[J]. Physical Review Letters, 2005, 95(4):040401. doi: 10.1103/PhysRevLett.95.040401 [4] GOPAL R, SIMEONIDIS K, MOSHAMMER R, et al.. Three-dimensional momentum imaging of electron wave packet interference in few-cycle laser pulses[J]. Physical Review Letters, 2009, 103(5):053001. doi: 10.1103/PhysRevLett.103.053001 [5] BIAN X B, HUISMANS Y, SMIRNOVA O, et al.. Subcycle interference dynamics of time-resolved photoelectron holography with midinfrared laser pulses[J]. Physical Review A, 2011, 84(4):043420. doi: 10.1103/PhysRevA.84.043420 [6] 陈建宏, 郑小平, 张正荣, 等.氢负离子在少周期激光场中解离时的干涉效应[J].物理学报, 2016, 65(8):083202. http://d.old.wanfangdata.com.cn/Periodical/wlxb201608013CHEN J H, ZHENG X P, ZHANG ZH R, et al.. Interference effect in the photodetachment from H- ion in a few-cycle laser pulse[J]. Acta Physica Sinica, 2016, 65(8):083202.(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/wlxb201608013 [7] ARBÓ D G, ISHIKAWA K L, SCHIESSL K, et al.. Intracycle and intercycle interferences in above-threshold ionization: the time grating[J]. Physical Review A, 2010, 81(2):021403(R). doi: 10.1103/PhysRevA.81.021403 [8] ARBÓ D G, ISHIKAWA K L, SCHIESSL K, et al.. Diffraction at a time grating in above-threshold ionization: the influence of the Coulomb potential[J]. Physical Review A, 2010, 82(4):043426. doi: 10.1103/PhysRevA.82.043426 [9] SONG X H, XU J W, LIN CH, et al.. Attosecond interference induced by Coulomb-field-driven transverse backward-scattering electron wave packets[J]. Physical Review A, 2017, 95(3):033426. doi: 10.1103/PhysRevA.95.033426 [10] YANG W F, ZHANG H T, LIN CH, et al.. Momentum mapping of continuum-electron wave-packet interference[J]. Physical Review A, 2016, 94(4):043419. doi: 10.1103/PhysRevA.94.043419 [11] BLAGA C I, CATOIRE F, COLOSIMO P, et al.. Strong-field photoionization revised[J]. Nature Physics, 2009, 5(5):335-338. doi: 10.1038/nphys1228 [12] QUAN W, LIN Z, WU M, et al.. Classical aspects in above-threshold ionization with a midinfrared strong laser field[J]. Physical Review Letters, 2009, 103(9):093001. doi: 10.1103/PhysRevLett.103.093001 [13] GUO L, HAN S S, LIU X, et al.. Scaling of the low-energy structure in above-threshold ionization in the tunneling regime:theory and experiment[J]. Physical Review Letters, 2013, 110(1):013001. doi: 10.1103/PhysRevLett.110.013001 [14] MORISHITA T, CHEN ZH J, WATANABE S, et al.. Two-dimensional electron momentum spectra of argon ionized by short intense lasers: comparison of theory with experiment[J]. Physical Review A, 2007, 75(2):023407. doi: 10.1103/PhysRevA.75.023407 [15] CHEN ZH J, MORISHITA T, LE A T, et al.. Analysis of two-dimensional high-energy photoelectron momentum distributions in the single ionization of atoms by intense laser pulses[J]. Physical Review A, 2007, 76(4):043402. doi: 10.1103/PhysRevA.76.043402 [16] GUO ZH J, CHEN ZH J, ZHOU X X. Origin of diffraction fringes in two-dimensional photoelectron momentum distributions for single ionization of atoms in few-cycle intense laser pulses[J]. Chinese Physics B, 2014, 23(4):043201. doi: 10.1088/1674-1056/23/4/043201 [17] ARBÓ D G, NAGELE S, TONG X M, et al.. Interference of electron wave packets in atomic ionization by subcycle sculpted laser pulses[J]. Physical Review A, 2014, 89(4):043414. doi: 10.1103/PhysRevA.89.043414 [18] 肖相如, 王慕雪, 黎敏, 等.强激光场中原子单电离的半经典方法[J].物理学报, 2016, 65(22):220203. doi: 10.7498/aps.65.220203XIAO X R, WANG M X, LI M, et al.. Semiclassical methods for strong field ionization of atoms[J]. Acta Physica Sinica, 2016, 65(22):220203.(in Chinese) doi: 10.7498/aps.65.220203 [19] CHEN ZH J, MORISHITA T, LE A T, et al.. Analysis of two-dimensional photoelectron momentum spectra and the effect of the long-range Coulomb potential in single ionization of atoms by intense lasers[J]. Physical Review A, 2006, 74(5):053405. doi: 10.1103/PhysRevA.74.053405 -
下载:
图(7)
计量
- 文章访问数: 1642
- HTML全文浏览量: 673
- PDF下载量: 55
- 被引次数: 0
