基于离轴自由曲面的激光通信光学天线设计

谷茜茜; 崔占刚; 亓波

doi:10.3788/CO.2019-0157

基于离轴自由曲面的激光通信光学天线设计

doi: 10.3788/CO.2019-0157

谷茜茜^{1, 2, 3,},
崔占刚^{1, 2, 3,},
亓波^{1, 2, 3, ,}

1.
中国科学院光束控制重点实验室，四川成都 610209
2.
中国科学院光电技术研究所，四川成都 610209
3.
中国科学院大学，北京 100049

基金项目: 中国科学院创新基金（No. CXJJ-19S008）

详细信息

作者简介:
谷茜茜(1993—)，女，河北石家庄人，硕士研究生，2017年于长春理工大学获得学士学位，主要从事激光通信光学系统设计方面的研究。E-mail：gu_xi_xi@126.com

亓　波(1978—)，男，山东莱芜人，博士，研究员，博士生导师，主要从事光学工程，光学精密机械等方面的研究。E-mail：qibo@ioe.ac.cn

中图分类号: TP394.1；TH691.9
计量
- 文章访问数: 3211
- HTML全文浏览量: 1198
- PDF下载量: 214
- 被引次数: 0
出版历程
- 收稿日期: 2019-07-25
- 修回日期: 2019-09-15
- 刊出日期: 2020-06-01

Design of optical antenna for laser communication based on an off-axis freeform surface

GU Xi-xi^{1, 2, 3
,},
CUI Zhan-gang^{1, 2, 3
,},
QI Bo^{1, 2, 3
, ,}

1.
Key Laboratory of Beam Control, Chinese Academy of Sciences, Chengdu 610209, China
2.
Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu 610209, China
3.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: Supported by CAS Innovation Project of China (No. CXJJ-19S008)

More Information

Corresponding author: qibo@ioe.ac.cn

摘要

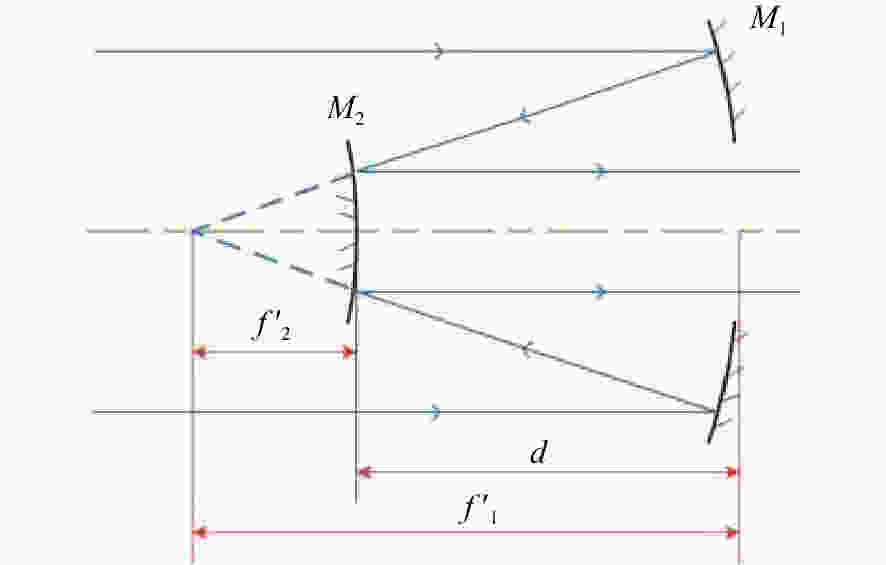
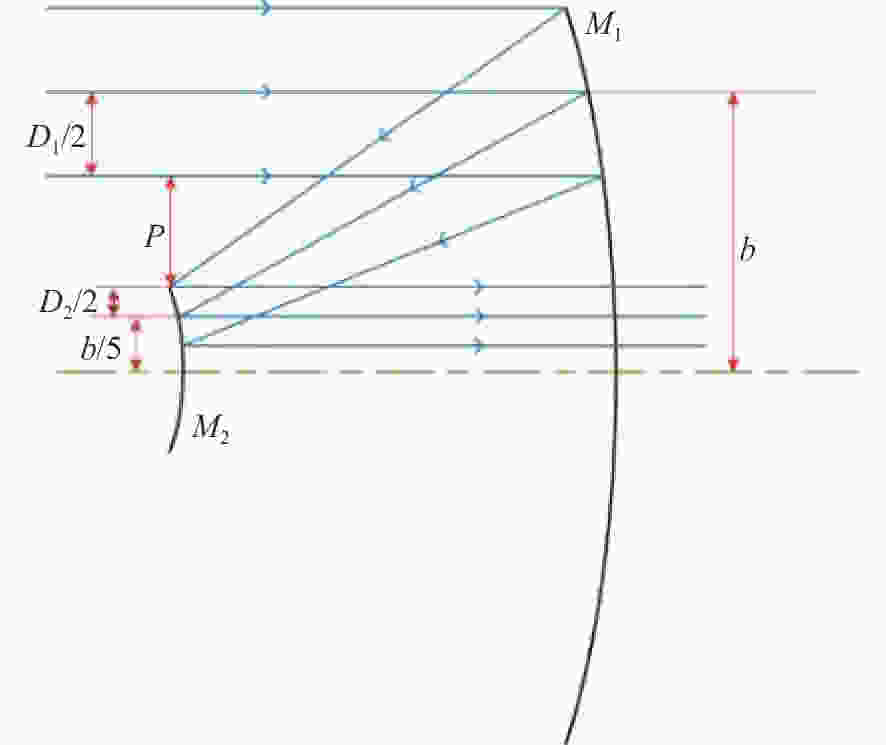
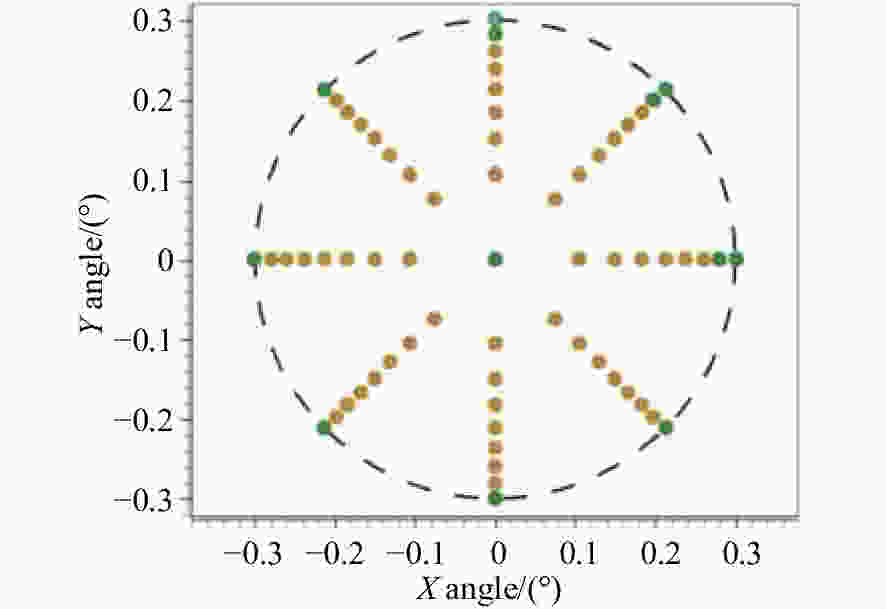
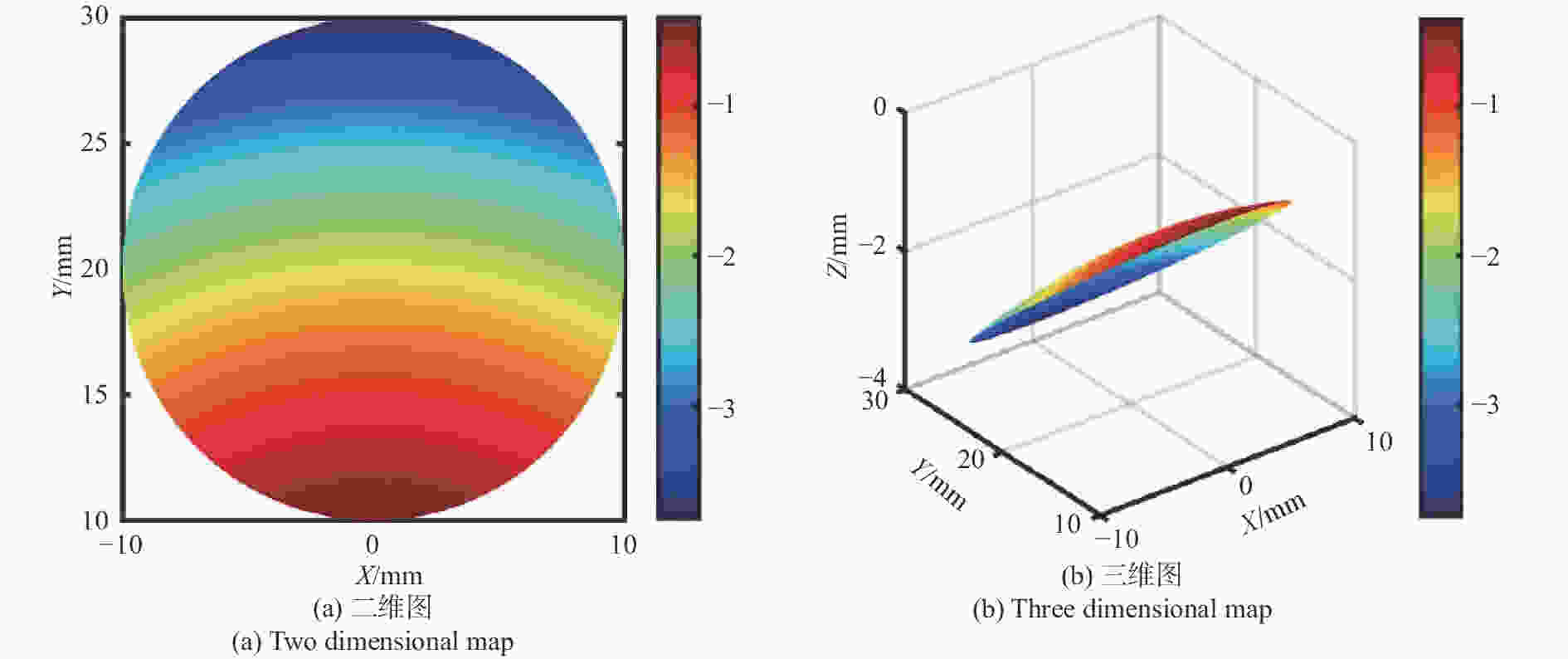
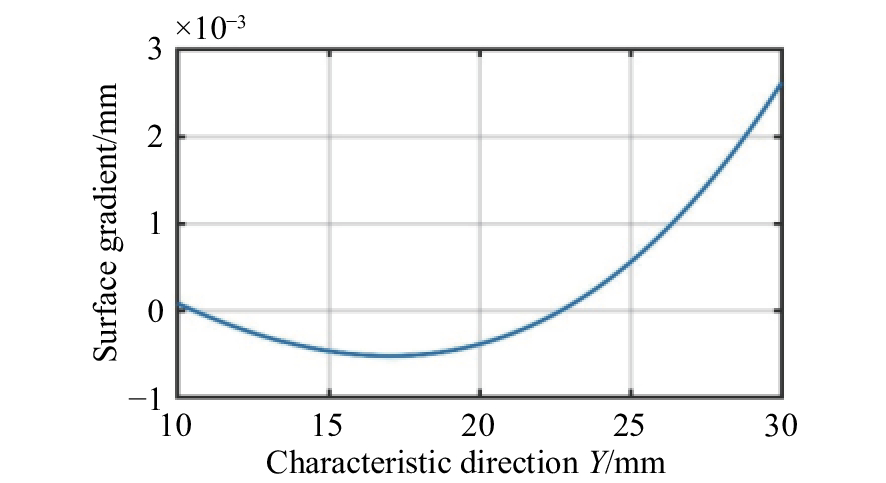
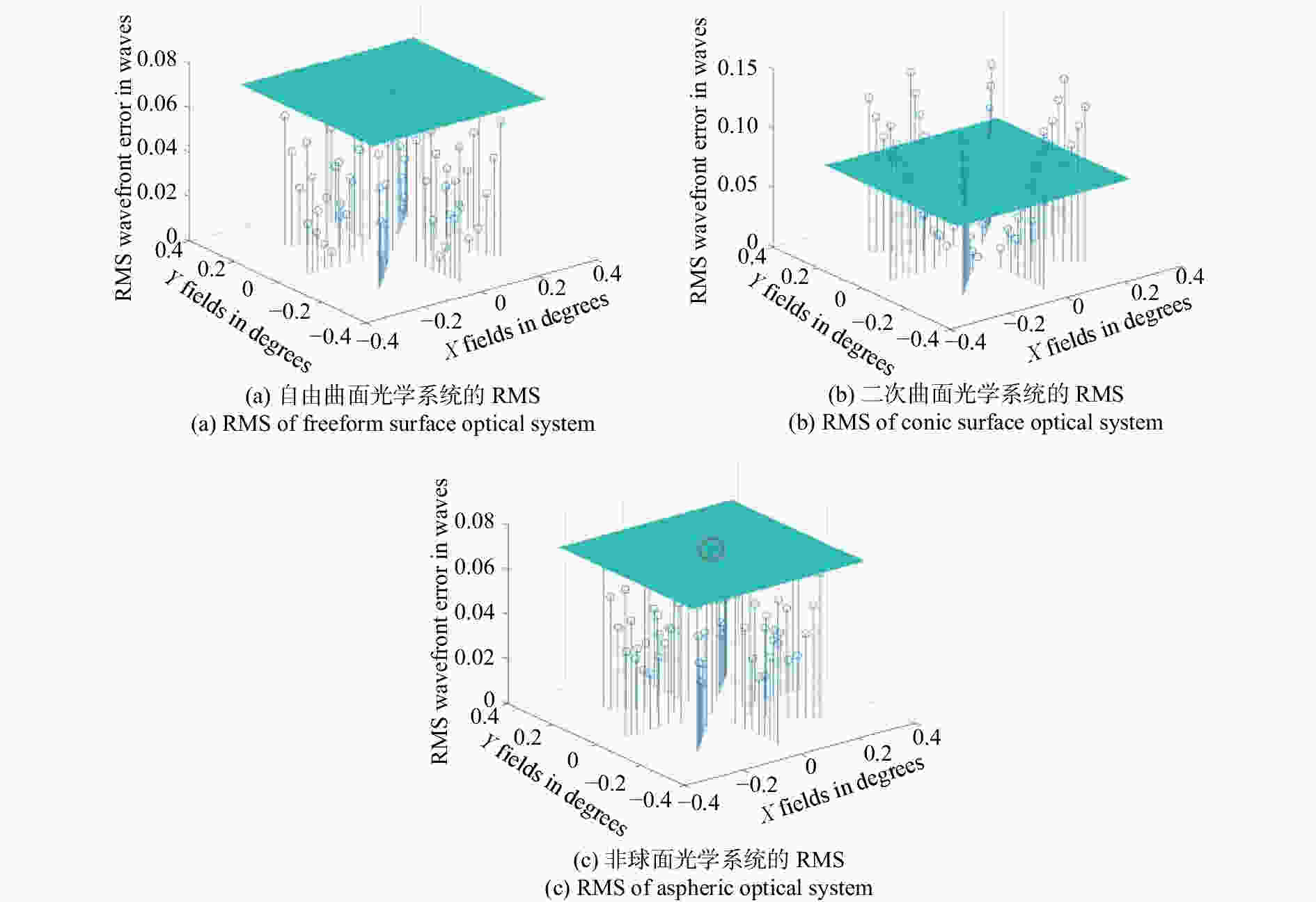
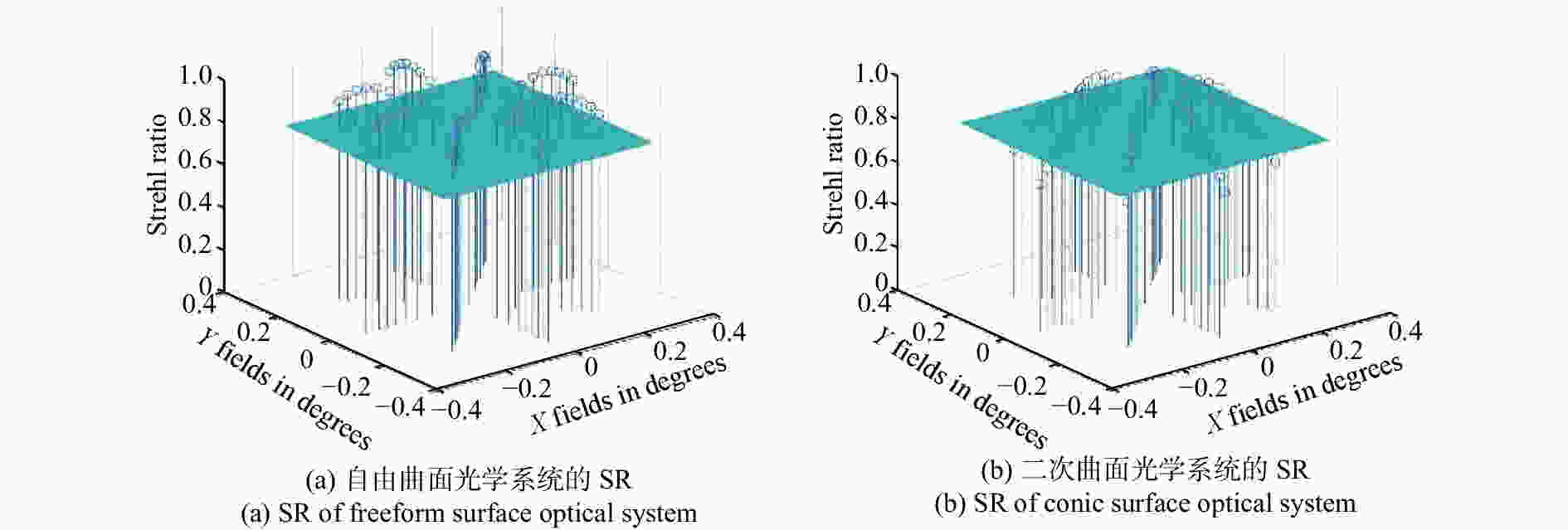
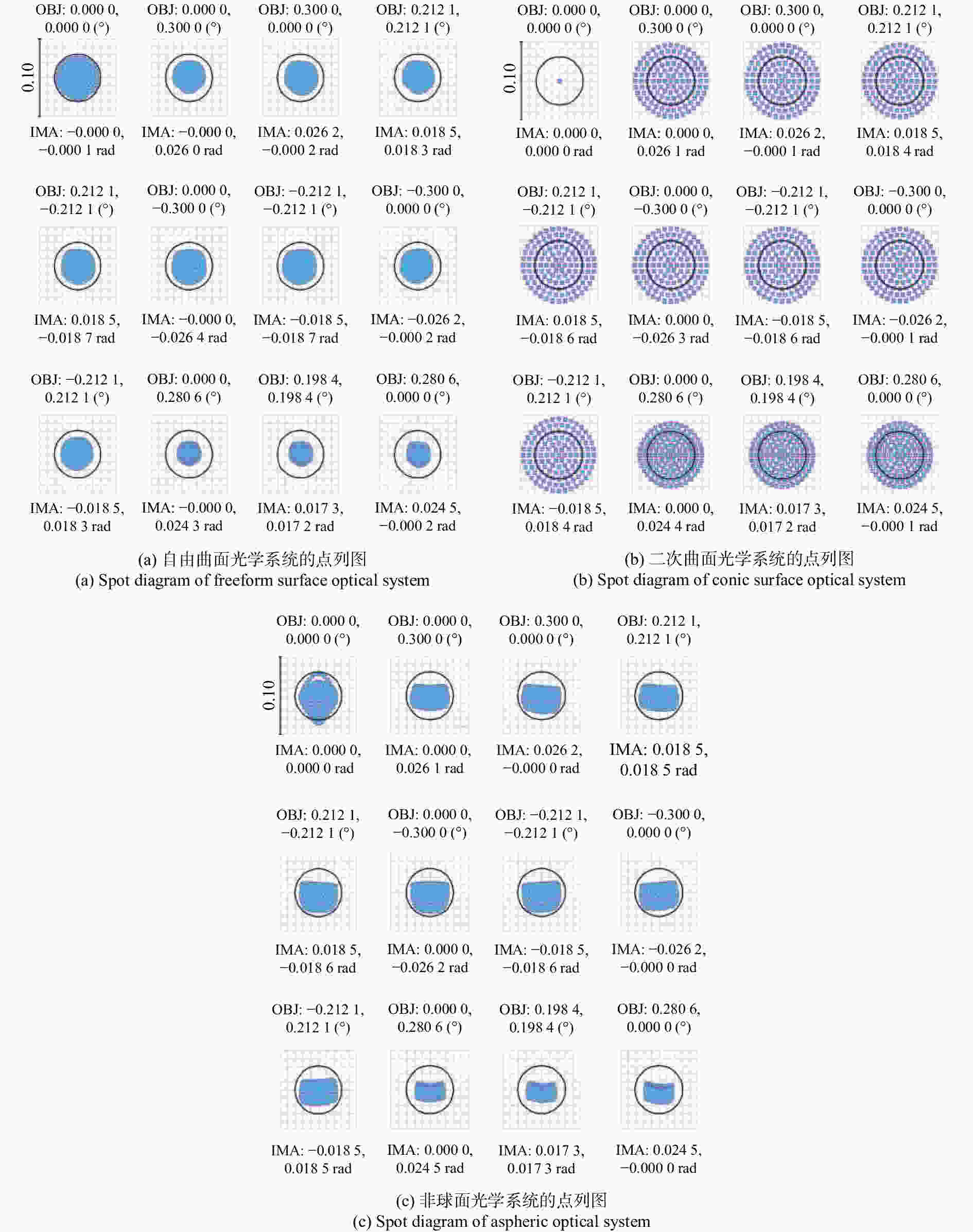
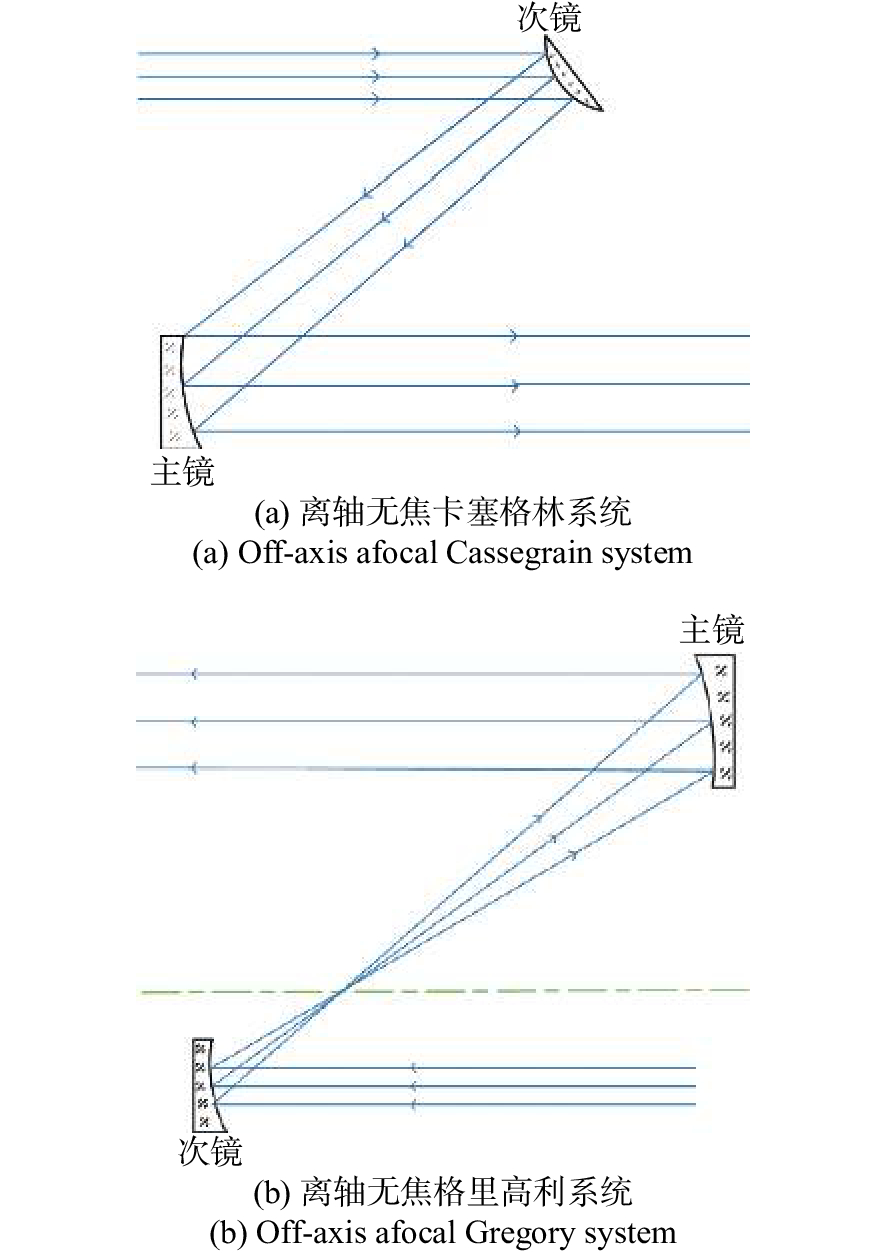
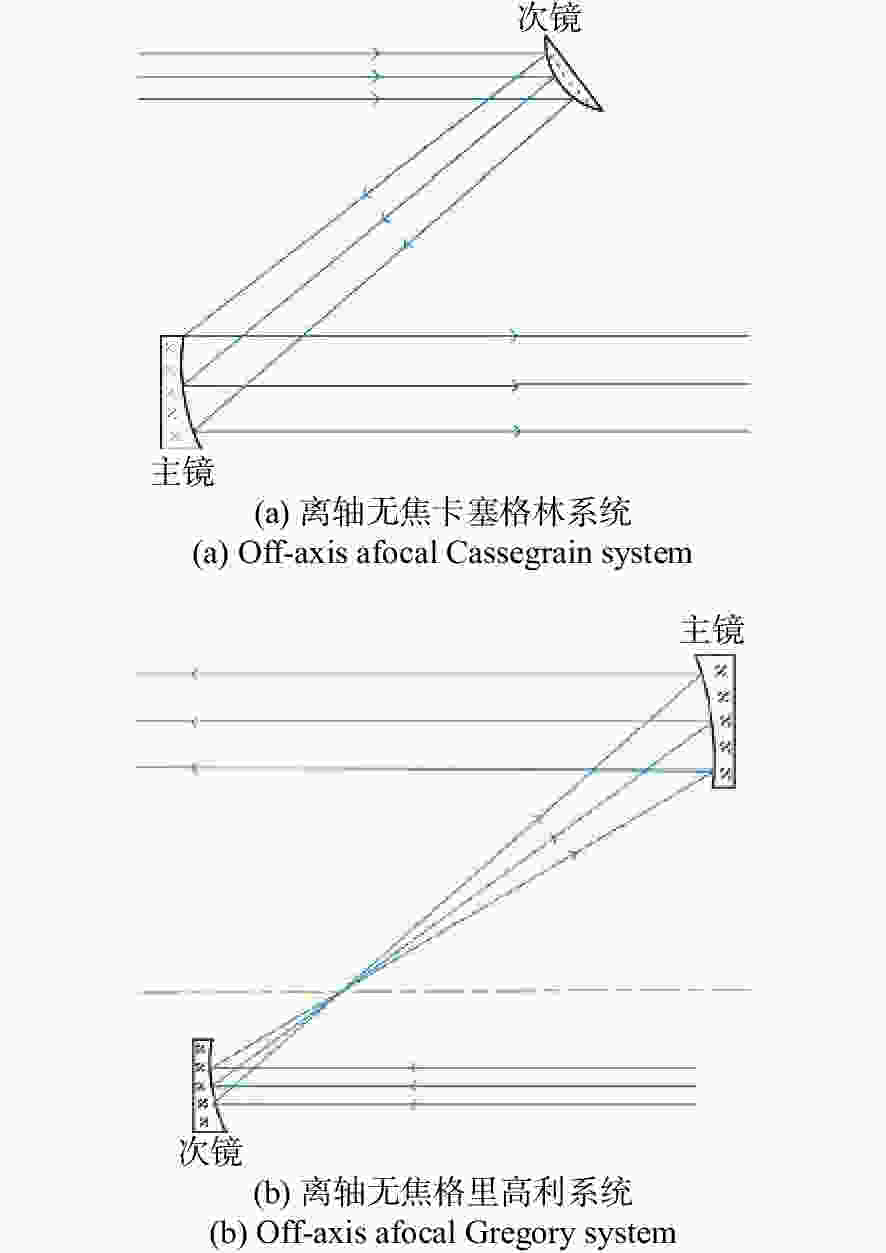
摘要: 为了提高空间激光通信系统的工作范围，简化光学系统的结构，提出了基于离轴自由曲面的大视场两镜无焦光学天线的设计形式。该光学天线采用无焦结构，无需再使用准直透镜元件，可以极大地简化系统结构，克服了传统聚焦光学天线体积过大、大功率光源情况下焦点处功率密度过高等问题。首先，基于三级像差理论，推导了两镜无焦系统的消像差公式，并对求解结果进行了分析总结。然后，根据求解结果和实际需求设计了一款无焦光学天线，该系统的有效通光口径为100 mm，放大倍率为5倍，波段为500~1 100 nm，全视场角为0.6°，主镜为凹抛物面的一部分，次镜采用XY多项式表征的自由曲面，并用MATLAB 对次镜自由曲面面形进行了仿真。结果表明，光学系统全视场的波像差优于λ/14（λ=500 nm），斯托列尔比大于0.8，系统能量集中度较高，像质接近衍射极限，光学视场相对于传统二次曲面系统增加了26.7%。因此，该种天线结构在激光通信领域具有较强的实用性和很好的发展前景。
- 光学天线设计 /
- 大视场 /
- 自由曲面 /
- 离轴两镜无焦系统
Abstract: We propose a design for a large-field two-mirror afocal optical antenna based on an off-axis freeform surface to improve the working range of space laser communication systems and simplify the structure of optical systems. The optical antenna adopts an afocal structure without using collimating lens elements, which can greatly simplify the system structure, overcome the problems of traditional focusing optical antennae such as them being too large in volume or having a power density that is too high at the focus when using high power light source. First, based on third-order aberration theory, the aberration-free formula of this class of two-mirror afocal optical antenna is derived, and relative results are analyzed. Then, an afocal optical antenna is designed according to the analyzed results and practical requirements. The effective aperture of the system is 100 mm, the magnification is 5, the range of the wavelength is 500~1 100 nm, the full field of view is 0.6°, the primary mirror is part of the concave paraboloid and the secondary mirror is a freeform surface characterized by XY polynomials. MATLAB software is used to simulate the freeform surface of the secondary mirror. The design results show that the total field of view wavefront error of the optical system is better than λ/14 (λ=500 nm), the Strehl ratio is greater than 0.8, the system has a higher energy concentration, and the image quality is close to the diffraction limit. The field of view of the freeform surface optical system increased by 26.7% compared with that using traditional conic surface system. Therefore, this antenna structure is highly applicable and shows strong prospects for development in the field of laser communication.
- optical antenna design /
- large field of view /
- freeform surface /
- off-axis two-mirror afocal system

HTML全文

图 1 离轴两镜无焦系统的两种结构

Figure 1. Structures of two kinds of off-axis two-mirror afocalsystems

下载: 全尺寸图片幻灯片

图 2 同轴两镜无焦系统示意图

Figure 2. Schematic of coaxial two-mirror afocal system

下载: 全尺寸图片幻灯片

图 3 离轴量示意图

Figure 3. Schematic of off-axis distance

下载: 全尺寸图片幻灯片

图 4 视场采样图

Figure 4. Field sampling map

下载: 全尺寸图片幻灯片

图 5 光学系统结构图

Figure 5. Layout of the optical system

下载: 全尺寸图片幻灯片

图 6 次镜XY自由曲面的二维和三维面形图

Figure 6. 2-D and 3-D profiles of XY freeform surface for secondary mirror

下载: 全尺寸图片幻灯片

图 7 次镜的面形梯度

Figure 7. Surface gradient of secondary mirror

下载: 全尺寸图片幻灯片

图 8 光学系统的RMS波像差

Figure 8. RMS wavefront errors of different optical systems

下载: 全尺寸图片幻灯片

图 9 光学系统的斯托列尔比（SR）

Figure 9. Strehl Ratios (SR) of different optical systems

下载: 全尺寸图片幻灯片

图 10 光学系统点列图

Figure 10. Spot diagrams of different optical systems

下载: 全尺寸图片幻灯片

图 11 不同光学系统的MTF

Figure 11. MTFs of different optical systems

下载: 全尺寸图片幻灯片

表 1 次镜自由曲面参数

Table 1. Polynomial parameters of freeform surface for secondary mirror

Item	Coefficient A_i	Item	Coefficient A_i
X¹Y⁰	0	X³Y¹	0
X⁰Y¹	6.735 780×10^–5	X²Y²	6.216 308×10^–9
X²Y⁰	0	X¹Y³	0
X¹Y¹	0	X⁰Y⁴	1.616 430×10^–9
X⁰Y²	0	X⁵Y⁰	0
X³Y⁰	0	X⁴Y¹	−2.079 343×10^–11
X²Y¹	−1.055 768×10^–7	X³Y²	0
X¹Y²	0	X²Y³	−1.129 752×10^–10
X⁰Y³	−4.533 126×10^–8	X¹Y⁴	0
X⁴Y⁰	5.532 042×10^–11	X⁰Y⁵	−1.957 926×10^–11

下载: 导出CSV

参考文献(24)

[1]	姜会林, 佟首峰, 张立中, 等. 空间激光通信技术与系统[M]. 北京: 国防工业出版社, 2010. JIANG H L, TONG SH F, ZHANG L ZH, et al.. The Technologies and Systems of Space Laser Communication[M]. Beijing: National Defense Industry Press, 2010. (in Chinese)
[2]	金光, 李艳杰, 钟兴, 等. 空间成像与激光通信共口径光学系统设计[J]. 光学精密工程,2014,22(8):2067-2074. doi: 10.3788/OPE.20142208.2067 JIN G, LI Y J, ZHONG X, et al. Design of co-aperture optical system for space imaging and laser communication[J]. Optics and Precision Engineering, 2014, 22(8): 2067-2074. (in Chinese) doi: 10.3788/OPE.20142208.2067
[3]	肖海桥, 张量, 汤俊雄. 卫星光通信链路新型宽视场角捕捉方案探讨[J]. 电子学报,1999,27(8):56-59. doi: 10.3321/j.issn:0372-2112.1999.08.016 XIAO H Q, ZHANG L, TANG J X. A new wide field-of-view acquistion approach in inter-satellite laser link establishing[J]. Acta Electronica Sinica, 1999, 27(8): 56-59. (in Chinese) doi: 10.3321/j.issn:0372-2112.1999.08.016
[4]	JURANEK H J, SAND R, SCHWEIZER J, et al. Off-axis telescopes: the future generation of earth observation telescopes[J]. Proceedings of SPIE, 1998, 3439: 104-115. doi: 10.1117/12.325617
[5]	王蕴琦, 刘伟奇, 付瀚毅, 等. 离轴式共口径激光通信光学系统设计[J]. 激光与光电子学进展,2018,55(1):010602. WANG Y Q, LIU W Q, FU H Y, et al. Design of laser communication optical system with off-axis common aperture[J]. Laser &Optoelectronics Progress, 2018, 55(1): 010602. (in Chinese)
[6]	孙权社, 赵发财, 陈坤峰, 等. 空间激光通信系统离轴天线设计研究[J]. 红外与激光工程,2015,44(8):2501-2505. doi: 10.3969/j.issn.1007-2276.2015.08.044 SUN Q SH, ZHAO F C, CHEN K F, et al. Design of off-axis optical antenna for space optical communications[J]. Infrared and Laser Engineering, 2015, 44(8): 2501-2505. (in Chinese) doi: 10.3969/j.issn.1007-2276.2015.08.044
[7]	王伟. 自由曲面离轴反射式光学系统设计[D]. 南京: 南京理工大学, 2016. WANG W. Design of off-axis reflective optical system with freeform surface[D]. Nanjing: Nanjing University of Science & Technology, 2016. (in Chinese)
[8]	GAUTAM S, GUPTA A, SINGH G S. Optical design of off-axis Cassegrain telescope using freeform surface at the secondary mirror[J]. Optical Engineering, 2015, 54(2): 025113. doi: 10.1117/1.OE.54.2.025113
[9]	关姝, 王超, 佟首峰, 等. 空间激光通信离轴两镜反射望远镜自由曲面光学天线设计[J]. 红外与激光工程,2017,46(12):01222003. doi: 10.3788/IRLA201746.1222003 GUAN SH, WANG CH, TONG SH F, et al. Optical antenna design of off-axis two-mirror reflective telescope with freeform surface for space laser communication[J]. Infrared and Laser Engineering, 2017, 46(12): 01222003. (in Chinese) doi: 10.3788/IRLA201746.1222003
[10]	田永明, 王永志, 姜义君, 等. 星间激光通信信标跟踪无焦光学系统设计[J]. 制导与引信,2016,37(4):54-57. doi: 10.3969/j.issn.1671-0576.2016.04.011 TIAN Y M, WANG Y ZH, JIANG Y J, et al. The design of afocal optical system of beacon tracking system in inter-satellite laser communication[J]. Guidance &Fuze, 2016, 37(4): 54-57. (in Chinese) doi: 10.3969/j.issn.1671-0576.2016.04.011
[11]	王红亚. 大气激光通信系统及其主要部件的研究[D]. 天津: 天津大学, 2005. WANG H Y. Research on free space optical communication system and its major components[D]. Tianjin: Tianjin University, 2005. (in Chinese)
[12]	武越. 离轴反射式扩束系统研究[D]. 长春: 长春理工大学, 2016. WU Y. Research of off-axis reflection beam expander[D]. Changchun: Changchun University of Science and Technology, 2016. (in Chinese)
[13]	王灵杰, 张新, 张建萍, 等. 自由曲面空间光学系统设计研究[J]. 应用光学,2012,33(6):1040-1046. WANG L J, ZHANG X, ZHANG J P, et al. Free-form surface space optical system[J]. Journal of Applied Optics, 2012, 33(6): 1040-1046. (in Chinese)
[14]	朱钧, 吴晓飞, 侯威, 等. 自由曲面在离轴反射式空间光学成像系统中的应用[J]. 航天返回与遥感,2016,37(3):1-8. doi: 10.3969/j.issn.1009-8518.2016.03.001 ZHU J, WU X F, HOU W, et al. Application of freeform surfaces in designing off-axis reflective space optical imaging systems[J]. Spacecraft Recovery &Remote Sensing, 2016, 37(3): 1-8. (in Chinese) doi: 10.3969/j.issn.1009-8518.2016.03.001
[15]	YE J F, CHEN L, LI X H, et al. Review of optical freeform surface representation technique and its application[J]. Optical Engineering, 2017, 56(11): 110901.
[16]	薛栋林, 郑立功, 张峰, 等. 基于光学自由曲面的离轴三反光学系统[J]. 光学精密工程,2011,19(12):2813-2820. doi: 10.3788/OPE.20111912.2813 XUE D L, ZHENG L G, ZHANG F, et al. Off-axis three-mirror system based on freeform mirror[J]. Optics and Precision Engineering, 2011, 19(12): 2813-2820. (in Chinese) doi: 10.3788/OPE.20111912.2813
[17]	倪栋伟, 李旭阳, 杨明洋, 等. 基于自由曲面的大视场天基探测光学系统[J]. 光学学报,2018,38(11):1122003. NI D W, LI X Y, YANG M Y, et al. Large field of view space-based optical detection system based on freeform surface[J]. Acta Optica Sinica, 2018, 38(11): 1122003. (in Chinese)
[18]	刘秀梅, 李红光. 离轴非球面无光焦度系统的设计[J]. 红外,2010,31(7):14-17. doi: 10.3969/j.issn.1672-8785.2010.07.003 LIU X M, LI H G. Design of off-axis aspheric non-power system[J]. Infrared, 2010, 31(7): 14-17. (in Chinese) doi: 10.3969/j.issn.1672-8785.2010.07.003
[19]	潘君骅. 光学非球面的设计、加工与检验[M]. 苏州: 苏州大学出版社, 2004. PAN J H. The Design, Manufacture and Test of the Aspherical Optical Surfaces[M]. Suzhou: Suzhou University Press, 2010. (in Chinese)
[20]	王涌天. 自由曲面光学系统设计及其应用[J]. 光学与光电技术,2012,10(3):13-16. WANG Y T. Design and application of free-curved surface optical system[J]. Optics &Optoelectronic Technology, 2012, 10(3): 13-16. (in Chinese)
[21]	张磊, 刘东, 师途, 等. 光学自由曲面面形检测技术[J]. 中国光学,2017,10(3):283-299. doi: 10.3788/co.20171003.0283 ZHANG L, LIU D, SHI T, et al. Optical free-form surfaces testing technologies[J]. Chinese Optics, 2017, 10(3): 283-299. (in Chinese) doi: 10.3788/co.20171003.0283
[22]	李旭阳, 倪栋伟, 杨明洋, 等. 基于自由曲面的大视场空间相机光学系统设计[J]. 光子学报,2018,47(9):922003. doi: 10.3788/gzxb20184709.0922003 LI X Y, NI D W, YANG M Y, et al. Design of large field of view space camera optical system based on freeform surfaces[J]. Acta Photonica Sinica, 2018, 47(9): 922003. (in Chinese) doi: 10.3788/gzxb20184709.0922003
[23]	王权陡, 余景池, 张学军, 等. 离轴非球面最接近球面半径及非球面度的求解[J]. 光电工程,2000,27(3):16-19. doi: 10.3969/j.issn.1003-501X.2000.03.005 WANG Q D, YU J CH, ZHANG X J, et al. Solution for best fitting spherical curvature radius and asphericity of off-axis aspherics[J]. Opto-Electronic Engineering, 2000, 27(3): 16-19. (in Chinese) doi: 10.3969/j.issn.1003-501X.2000.03.005
[24]	杜玉军, 任海霞, 刘中本. 光学非球面元件非球面度计算方法[J]. 应用光学,2002,23(5):42-45. DU Y J, REN H X, LIU ZH B. The method of calculation to asphericity of optical aspheric surface component[J]. Journal of Applied Optics, 2002, 23(5): 42-45. (in Chinese)