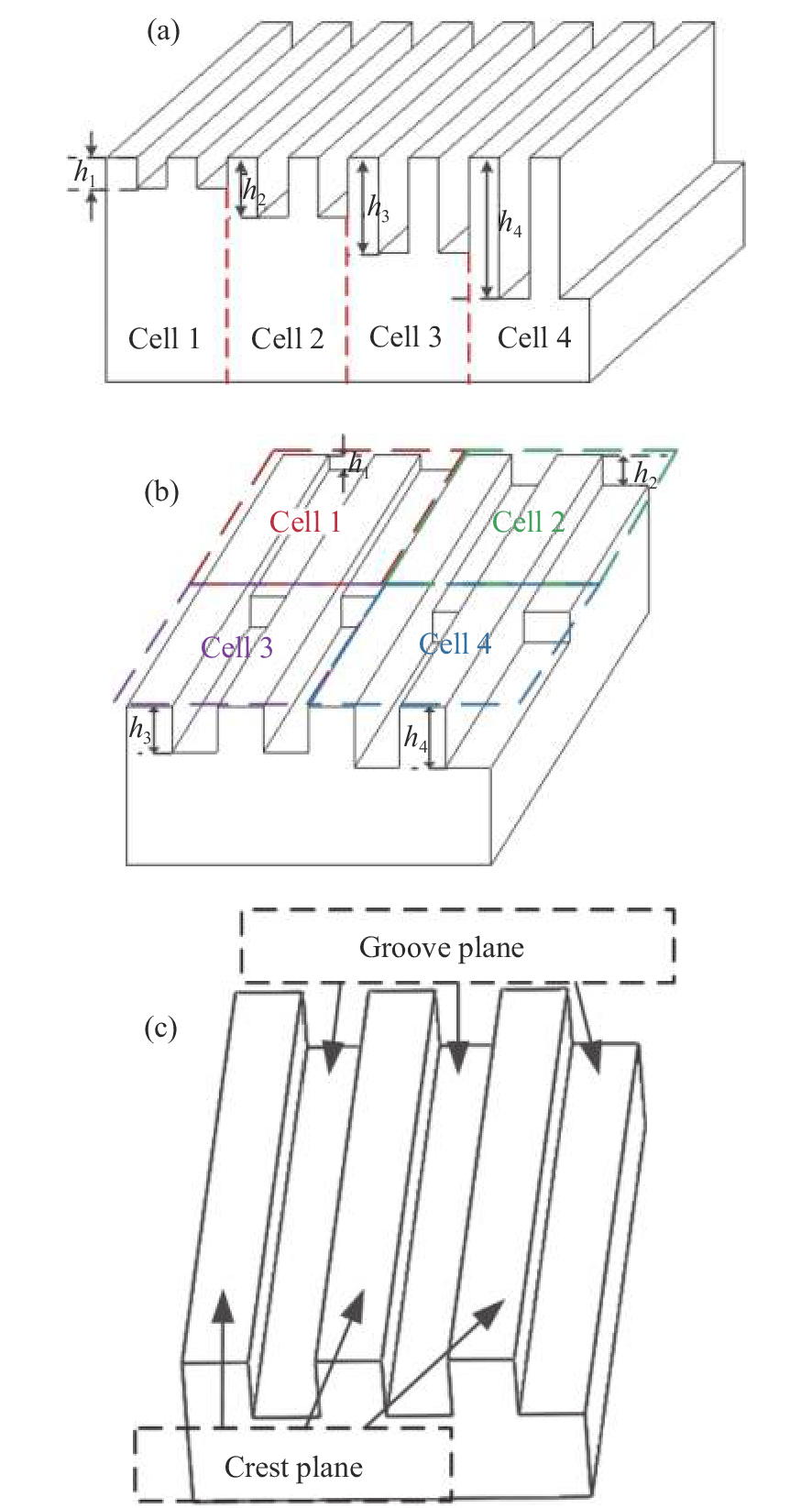
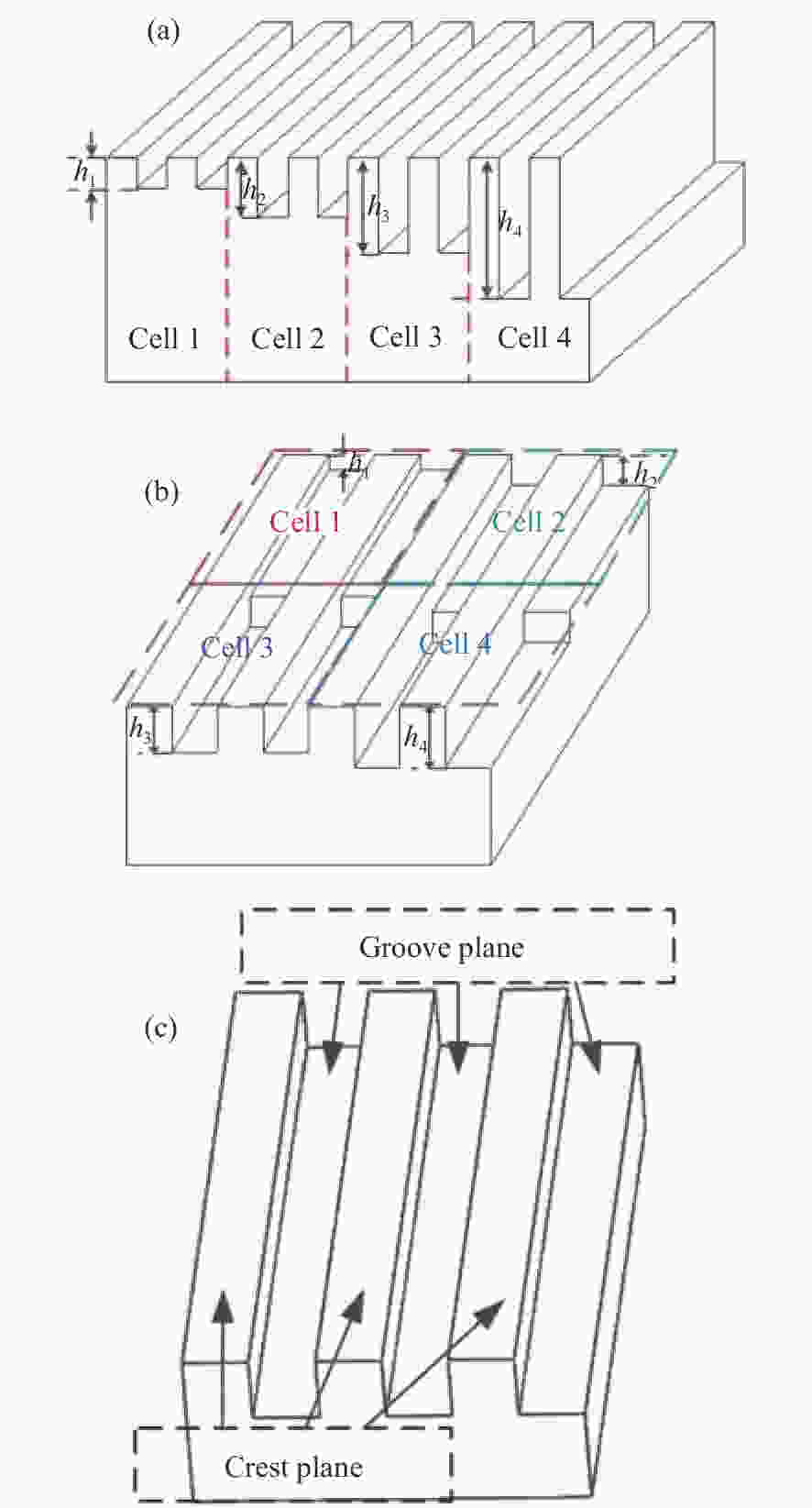
Diffraction characteristics analysis of multi-depth phase modulation grating in terahertz band
doi: 10.3788/CO.2019-0147
-
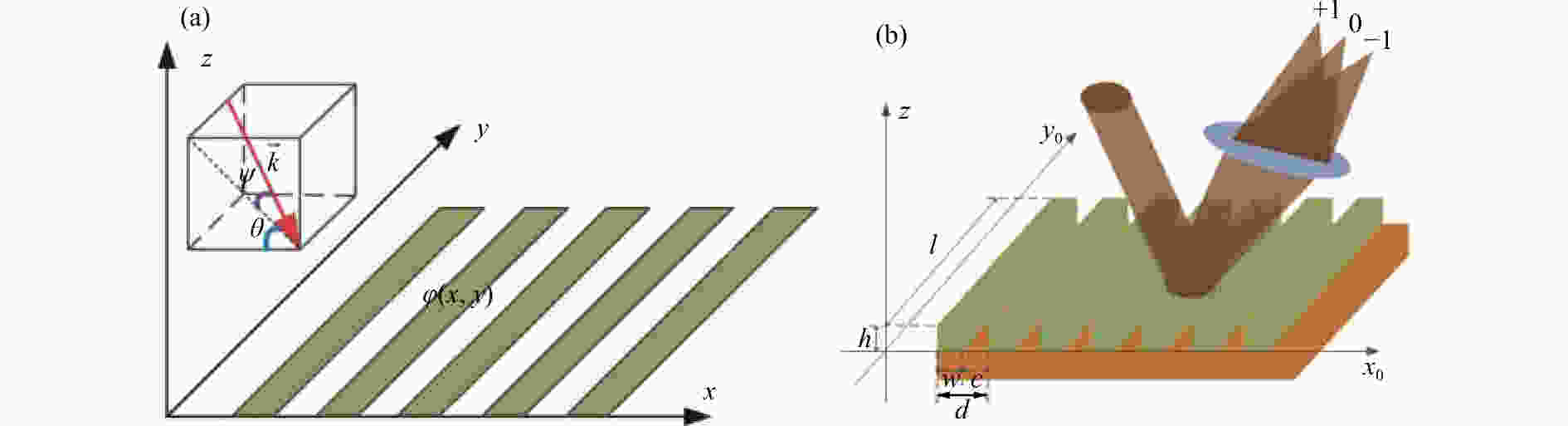
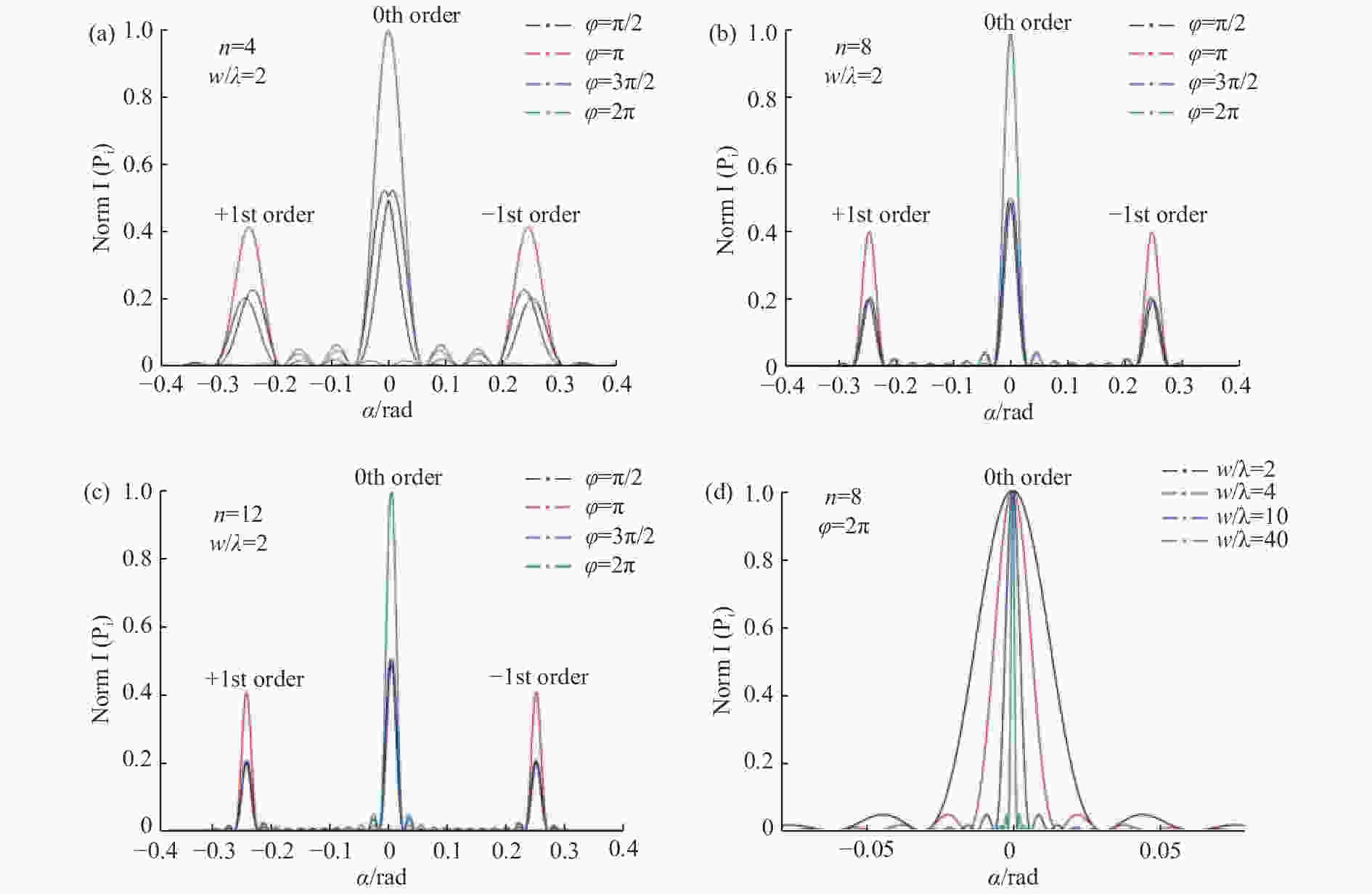
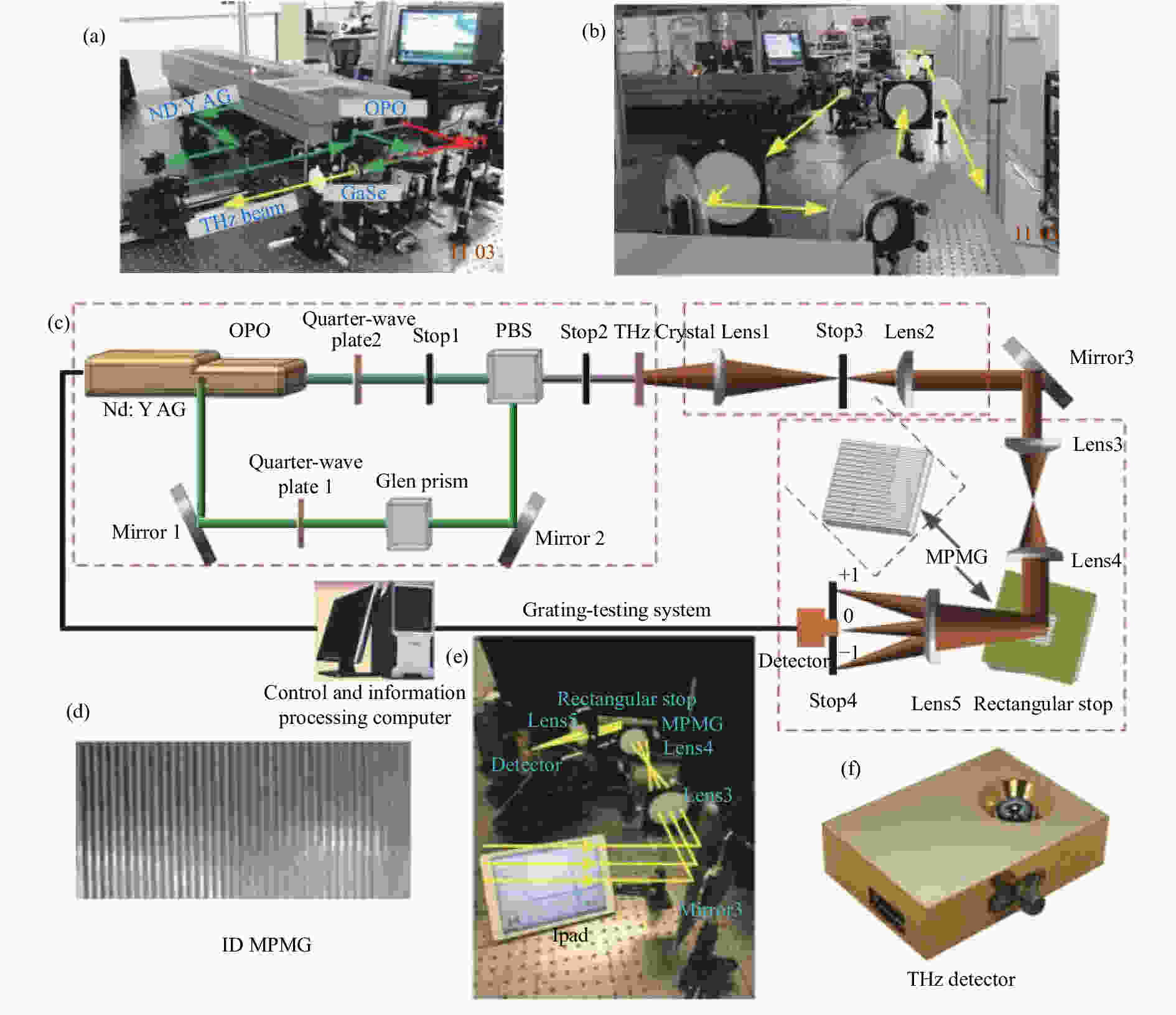
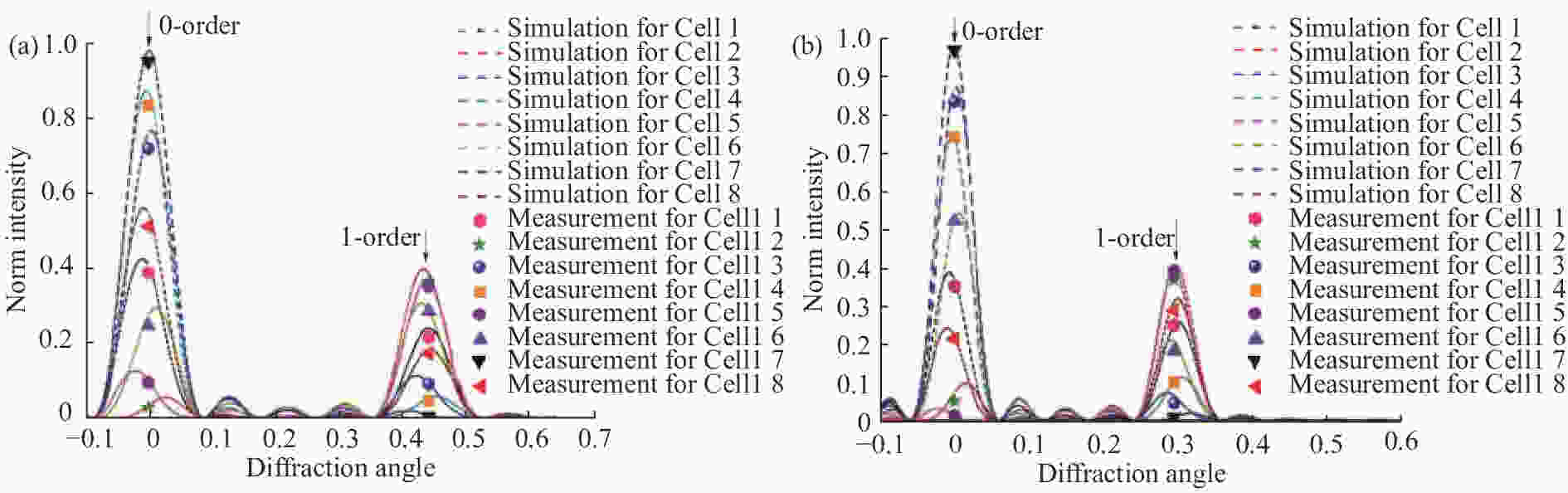
摘要: 针对太赫兹谱成像对宽光谱、高光能利用率、实时探测分光器件的需求，提出了一种太赫兹立体相位光栅（MPMG）分光器件。MPMG通过刻槽深度的变化引入光程差，实现对入射光的相位调制，从而使反射太赫兹波前的不同区域具有不同的相位信息，其零级衍射光具备分光能力。在分析MPMG衍射场光强分布的基础上，讨论了光栅参数对衍射场分布的影响，并通过实验验证了MPMG的衍射特性。结果表明，MPMG各光栅单元在0.5 THz、0.34 THz的衍射效率理论值与实测值相吻合，证明了MPMG的零级衍射光具备分光能力。Abstract: To meet the requirements of terahertz spectral imaging for wide spectral range, high efficiency and real-time detection of spectrometers, a Multi-depth Phase Modulation Grating (MPMG) in terahertz band is proposed. The phase modulation of incident light is realized by introducing optical path difference resulted from the change of groove depth, so that different regions of reflecting terahertz wave front have different phase information. Based on the analysis of the intensity distribution of the diffraction field of the MPMG, the influence of grating parameters on the distribution of the diffraction field is discussed. The diffraction characteristics of the MPMG are verified by experiments. The experiment results indicate that the measurements of the 0th- and ±1st-order diffraction efficiency at 0.5 and 0.34 THz obtained by experiment and simulation are in good agreement. It suggests that 0th order diffraction of the MPMG has the ability of splitting light.
-
Key words:
- THz /
- multi-depth phase modulation grating /
- fraunhofer diffraction /
- field distribution
-
图 1 MPMG示意图(a)一维MPMG，(b)二维MPMG(c)光栅单元
Figure 1. Schematic diagram of MPMG. (a) 1D MPMG, (b) 2D MPMG, (c) grating cell
图 2 (a) MPMG等效为平面透射光栅示意图 (b) MPMG衍射示意图
Figure 2. (a) Reflection grating simulated as a plane transmission grating; (b) MPMG diffraction diagram
图 3 不同相位调制下沿x轴方向的光强分布
Figure 3. Light intensity distributions along the x axis under different phase modulation conditions
图 4 (a) 高功率辐射源系统；(b) 激光准直与发射系统；(c) 实验方案；(d) 一维MPMG；(e) 光栅测试系统；(f) 探测器照片
Figure 4. (a) High-power THz radiation source system. (b) Laser collimation and transmission system. (c) Schematic of experiment. (d) 1D MPMG. (e) Grating-testing system. (f) Photograph of the THz detector.
图 5 光栅单元0级和1级衍射效率的模拟和测试结果(a) 0.34 THz (b) 0.5 THz
Figure 5. Simulation and test results of 0th- and 1st-order diffraction efficiency for each grating cell at (a) 0.34 THz and (b) 0.5 THz
表 1 Parameters of 1D MPMG
Table 1. Parameters of 1D MPMG
Name of parameter Value Name of parameter Value N 8 n 5 w /mm 1 l /mm 40 ψ/(°) 0 θ/(°) 60 h /cm h{1} 0.163 5 h{5} 0.817 5 h{2} 0.327 0 h{6} 0.981 0 h{3} 0.490 5 h{7} 1.144 5 h{4} 0.654 0 h{8} 1.308 0 
下载: 导出CSV
-
[1] ZHANG CH M, LI Q W, YAN Q L, et al. High throughput static channeled interference imaging spectropolarimeter based on a Savart polariscope[J]. Optics Express, 2016, 24(20): 23314-23332. doi: 10.1364/OE.24.023314 [2] LUO Y C, LIU X X, HAYTON D J, et al.. Fourier phase grating for THz multi-beam local oscillators[C]. Proceedings of the 26th International Symposium on Space Terahertz Technology, International Symposium on Space Terahertz Technology, 2015: 77-78. [3] MIRZAEI B, SILVA J R G, LUO Y C, et al. Efficiency of multi-beam Fourier phase gratings at 1.4 THz[J]. Optics Express, 2017, 25(6): 6581-6588. [4] WANG L, GE SH J, HU W, et al. Tunable reflective liquid crystal terahertz waveplates[J]. Optical Materials Express, 2017, 7(6): 2023-2029. doi: 10.1364/OME.7.002023 [5] YANG J, XIA T Y, JING SH CH, et al. Electrically tunable reflective terahertz phase shifter based on liquid crystal[J]. Journal of Infrared,Millimeter,and Terahertz Waves, 2018, 39(5): 439-446. doi: 10.1007/s10762-018-0469-3 [6] HALL R T, VRABEC D, DOWLING J M. A high-resolution, far infrared double-beam Lamellar grating interferometer[J]. Applied Optics, 1966, 5(7): 1147-1158. doi: 10.1364/AO.5.001147 [7] MANZARDO O, MICHAELY R, SCHÄDELIN F, et al. Miniature lamellar grating interferometer based on silicon technology[J]. Optics Letters, 2004, 29(13): 1437-1439. [8] YU H B, ZHOU G Y, SIONG C F, et al. An electromagnetically driven lamellar grating based Fourier transform microspectrometer[J]. Journal of Micromechanics and Microengineering, 2008, 18(5): 055016. doi: 10.1088/0960-1317/18/5/055016 [9] GAO X, LI SH H, MA Q L, et al. Development of grating-based precise displacement measurement technology[J]. Chinese Optics, 2019, 12(4): 741-752. (in Chinese) doi: 10.3788/co.20191204.0741 [10] ZHANG M, LV J G, LIANG J Q, et al. Error analysis and fabrication of low-stepped mirrors[J]. Chinese Optics, 2019, 12(4): 791-803. (in Chinese) doi: 10.3788/co.20191204.0791 [11] WU Y F, WANG Y J, SUN H J, et al. LSS-target detection in complex sky backgrounds[J]. Chinese Optics, 2019, 12(4): 853-865. (in Chinese) doi: 10.3788/co.20191204.0853 [12] Shanghai Institute of Technical Physics of the Chinese Academy of Sciences, CAS. Terahertz one-dimensional stereo phase grating: CN, CN106125176B[P]. 2018-06-26. (in Chinese) [13] HUANG J G, HUANG ZH M, TONG J CH, et al. Intensive terahertz emission from GaSe0.91S0.09 under collinear difference frequency generation[J]. Applied Physics Letters, 2013, 103(8): 081104. [14] YANG Q J, HE ZH P, SHU R. Lens design and verification used for terahertz space transmission[J]. Journal of Infrared and Millimeter Waves, 2017, 36(5): 519-525. doi: 10.11972/j.issn.1001-9014.2017.05.002 [15] HUANG Z M, HUANG J G, GAO Y Q, et al.. High-resolution terahertz spectrometer with up to 110 m single-pass base[C]. Proceedings of 2016 IEEE International Conference on Infrared, Millimeter, and Terahertz Waves, IEEE, 2016: 1-2. [16] XIAO ZH Y, YANG Q J, HUANG J G, et al. Terahertz communication windows and their point-to-point transmission verification[J]. Applied Optics, 2018, 57(27): 7673-7680. -
下载:
计量
- 文章访问数: 2413
- HTML全文浏览量: 1119
- PDF下载量: 105
- 被引次数: 0
