一种自适应安装的高精度图像式角位移测量装置

于海; 万秋华; 孙莹; 卢新然; 贾兴丹

doi:10.3788/CO.2019-0107

一种自适应安装的高精度图像式角位移测量装置

doi: 10.3788/CO.2019-0107

于海^1, ,,
万秋华¹,
孙莹¹,
卢新然¹,
贾兴丹^{1, 2}

1.
中国科学院长春光学精密机械与物理研究所，吉林长春 130033
2.
中国科学院大学，北京 100049

基金项目: 国家自然科学基金资助项目（No. 51605465）；吉林省科技发展计划资助项目（No. 20180520184JH）

详细信息

作者简介:
于　海（1987—），男，吉林敦化人，副研究员，2009年于东北电力大学获得学士学位，2014年于中国科学院长春光学精密机械与物理研究所机械电子工程专业获得工学博士学位，目前主要从事光电位移精密测量技术的研究。E-mail: yuhai@ciomp.ac.cn

通讯作者:
E-mail：yuhai@ciomp.ac.cn

中图分类号: TP212
计量
- 文章访问数: 1855
- HTML全文浏览量: 950
- PDF下载量: 76
- 被引次数: 0
出版历程
- 收稿日期: 2019-05-17
- 修回日期: 2019-07-16
- 刊出日期: 2020-06-01

A high precision image angular displacement measurement device with self-adaptive installation

YU Hai^{1
, ,},
WAN Qiu-hua¹,
SUN Ying¹,
LU Xin-ran¹,
JIA Xing-dan^{1, 2}

1.
Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: Supported by National Natural Science Foundation of China (No. 51605465); Science and Technology Development Programme of Jilin Province (No. 20180520184JH)

More Information

Corresponding author: yuhai@ciomp.ac.cn

摘要

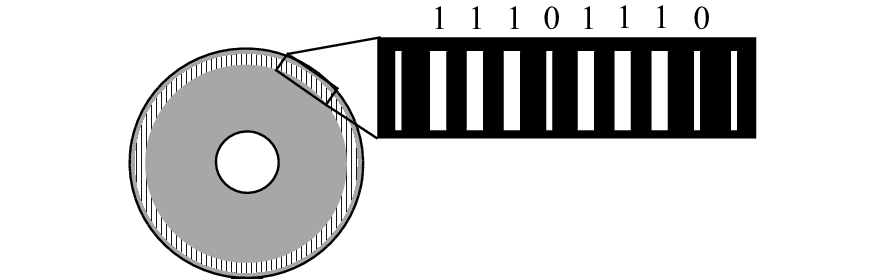
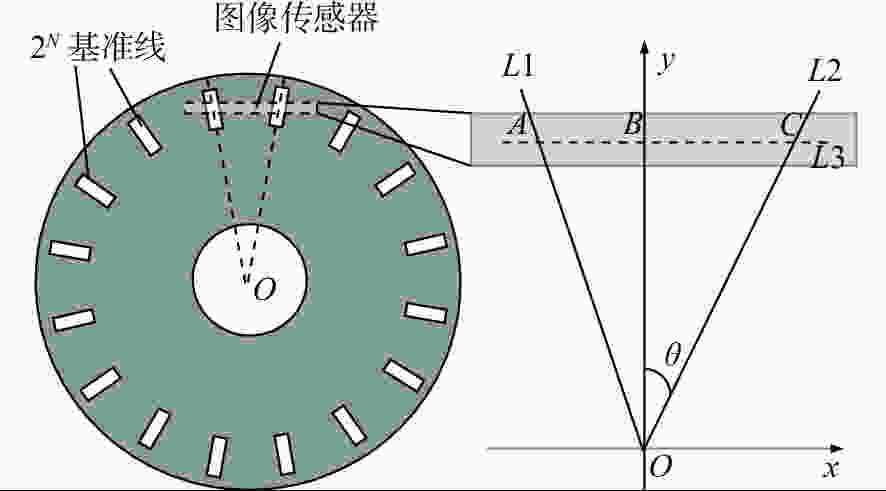
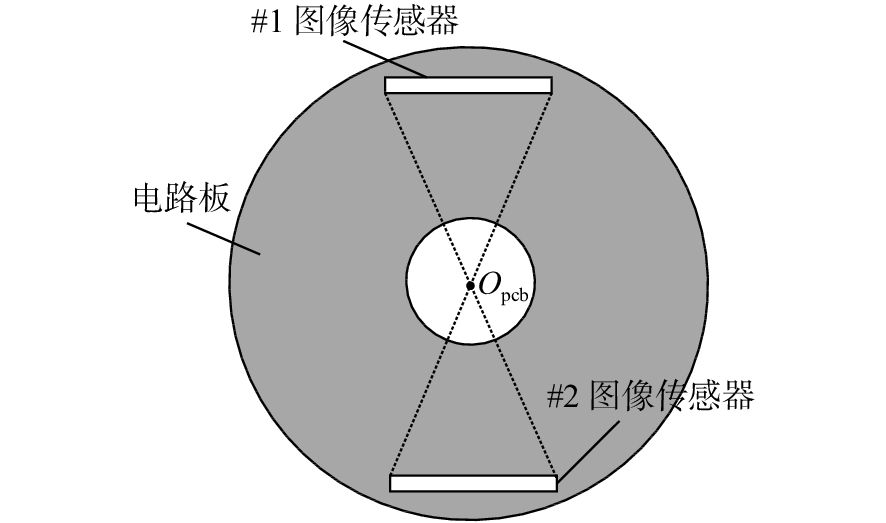
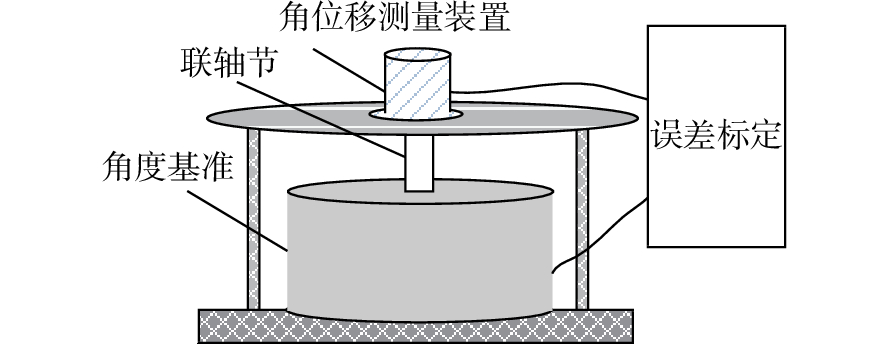
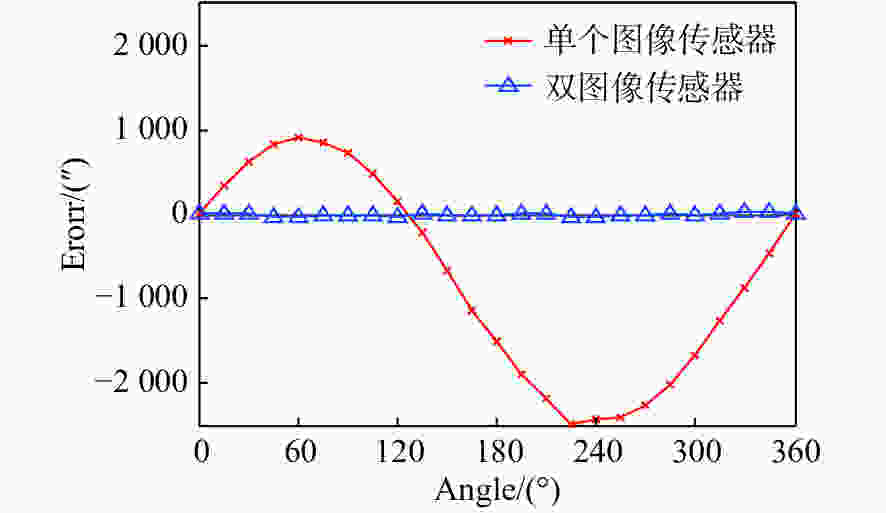
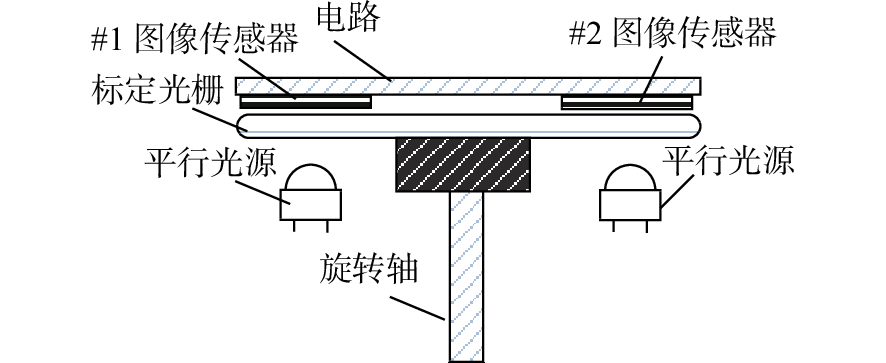
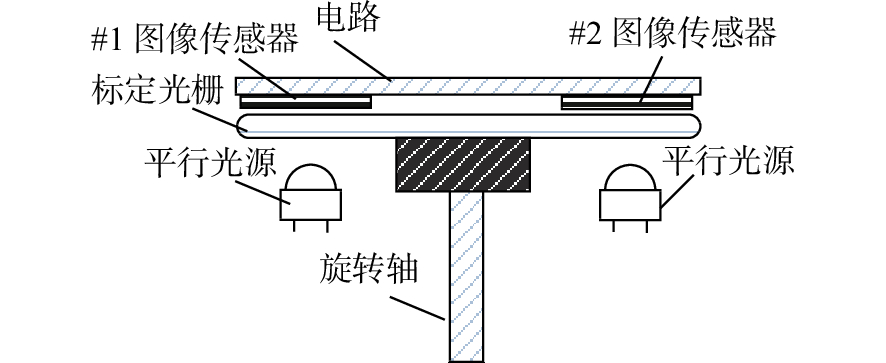
摘要: 采用图像探测器的角位移测量技术可实现高精度高分辨力角位移测量。为提高角位移测量装置的鲁棒性，本文设计了一种自适应安装的高精度图像式角位移测量装置。其装调过程非常简便，且可以保证在标定光栅存在偏心时具有高分辨力和高精度测量输出。首先，提出了基于双线阵图像传感器的测角装置设计原理，并设计了单圈绝对式标定光栅。然后，采用基于质心算法的高分辨力细分算法进行细分，并采用双线阵图像传感器对测角误差进行误差补偿。最后，设计实验装置测试自适应安装的性能。实验结果表明，当标定光栅的偏心度在±1 mm以内时，所设计装置可以实现高精度和高分辨力的角位移测量。本文所设计的装置可以在标定光栅存在±1 mm的安装偏心时保证输出精度，为小型角位移测量装置适应性的提高给出了解决方案。
- 角位移测量 /
- 误差补偿 /
- 双图像探测器 /
- 自适应安装
Abstract: The angular displacement measurement technology based on image detector is a hot research to realize high-precision and high-resolution angular displacement measurement. In order to improve the robustness of the angular displacement measuring devices, a high precision image displacement measurement device with self-adaptive installation techniques is designed in this paper. The installation and adjustment processes are very simple, and high resolution and high precision measurement output can be guaranteed in the presence of eccentricity in the calibration grating. Firstly, the angle measurement device using dual linear imaging sensors is proposed and a single-ring absolute grating is designed. Then, a high-resolution subdivision algorithm based on a centroid algorithm is used to subdivide the image, and dual linear image sensors are used to compensate for the angle measurement error. Finally, an experimental device is designed to test the performance of the adaptive installation. Experiments show that when the eccentricity of the grating is within ±1 mm, the designed device can achieve highly precise angular displacement measurements with high resolution. The device designed in this paper guarantee the output accuracy when the grating has an installation eccentricity of ±1 mm, which lays a foundation for improving the adaptability of small angular displacement measuring devices.
- angular displacement measurement /
- error compensation /
- dual image sensors /
- self-adaptive installation

HTML全文

图 1 测量光路原理图

Figure 1. Principle diagram of measuring optical path

下载: 全尺寸图片幻灯片

图 2 单圈编码原理图

Figure 2. Coding principle of single ring

下载: 全尺寸图片幻灯片

图 3 角位移细分原理

Figure 3. Angle subdivision principle

下载: 全尺寸图片幻灯片

图 4 图像传感器安装位置原理图

Figure 4. Principle diagram of image sensor installation position

下载: 全尺寸图片幻灯片

图 5 角位移测量装置

Figure 5. Angle measurement device

下载: 全尺寸图片幻灯片

图 6 文献[15]装置的分辨力检测曲线

Figure 6. Detection curve of the device in reference [15]

下载: 全尺寸图片幻灯片

图 7 精度测试原理

Figure 7. Principle of precision test

下载: 全尺寸图片幻灯片

图 8 单双图像传感器的误差对比

Figure 8. Comparison of measurement error by single- and dual- sensors

下载: 全尺寸图片幻灯片

图 9 实验装置的3次检测结果

Figure 9. Results of three tests on experimental equipment

下载: 全尺寸图片幻灯片

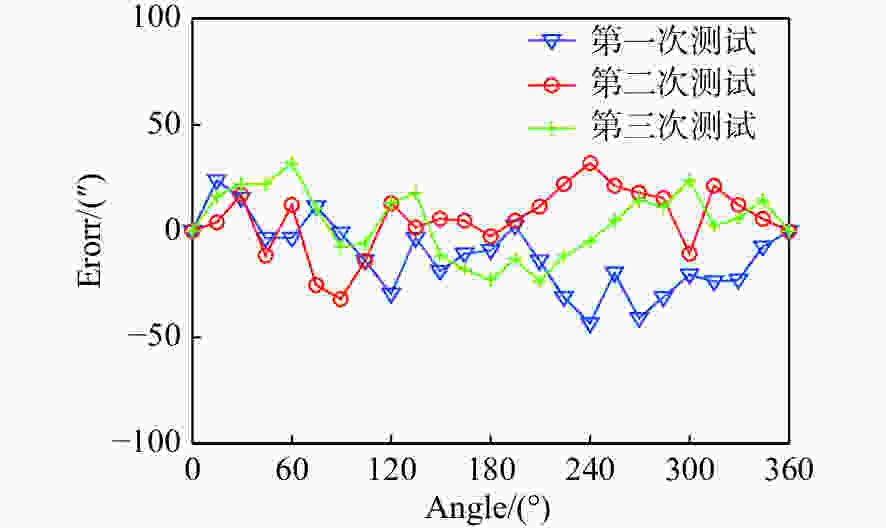
表 1 标定误差结果(″)

Table 1. Results of calibration error (″)

Angles/(°)	Errors	Angles/(°)	Errors	Angles/(°)	Errors
0	0	120	−28.1	240	−25.1
15	13.5	135	0.8	255	−2.1
30	6.9	150	−1.5	270	−11.2
45	−21.4	165	−2.0	285	12.3
60	−26.6	180	−6.1	300	−11.3
75	−17.2	195	5.6	315	16
90	−19.7	210	0.8	330	25.1
105	−12.2	225	−22	345	32.7

下载: 导出CSV

参考文献(16)

[1]	董莉莉, 熊经武, 万秋华. 光电轴角编码器的发展动态[J]. 光学精密工程,2000,8(2):198-202. DONG L L, XIONG J W, WAN Q H. Development of photoelectric rotary encoders[J]. Optics and Precision Engineering, 2000, 8(2): 198-202. (in Chinese)
[2]	叶盛祥. 光电位移精密测量技术[M]. 乌鲁木齐: 新疆科技卫生出版社, 2003. YE SH X. Optoelectronic Displacement Precision Measurement Technology[M]. Urumqi: Xinjiang Science and Technology Health Press, 2003. (in Chinese)
[3]	熊经武, 万秋华. 二十三位绝对式光电轴角编码器[J]. 光学机械,1990(2):52-60. XIONG J W, WAN Q H. A 23-bit absolute photo-electric rotary encoder[J]. Optics and Precision Engineering, 1990(2): 52-60. (in Chinese)
[4]	LEVITON D B, FREY B. Ultra-high resolution, absolute position sensors for cryostatic applications[J]. Proceedings of SPIE, 2003, 4850: 776-787. doi: 10.1117/12.461799
[5]	LEVITON D B, GARZA M S. Recent advances and applications of NASA's new, ultrahigh-sensitivity absolute optical pattern recognition encoders[J]. Proceedings of SPIE, 2000, 4091: 375-384. doi: 10.1117/12.405797
[6]	BAJIĆ J S, STUPAR D Z, DAKIĆ B M, et al. An absolute rotary position sensor based on cylindrical coordinate color space transformation[J]. Sensors and Actuators A:Physical, 2014, 213: 27-34. doi: 10.1016/j.sna.2014.03.036
[7]	SUGIYAMA Y, MATSUI Y, TOYODA H, et al. A 3.2 kHz, 14-bit optical absolute rotary encoder with a CMOS profile sensor[J]. IEEE Sensors Journal, 2008, 8(8): 1430-1436. doi: 10.1109/JSEN.2008.920709
[8]	TRESANCHEZ M, PALLEJÀ T, TEIXIDÓ M, et al. Using the image acquisition capabilities of the optical mouse sensor to build an absolute rotary encoder[J]. Sensors and Actuators A:Physical, 2010, 157(1): 161-167. doi: 10.1016/j.sna.2009.11.002
[9]	KIM J A, KIM J W, KANG C S, et al. Absolute angle measurement using a phase-encoded binary graduated disk[J]. Measurement, 2016, 80: 288-293. doi: 10.1016/j.measurement.2015.11.037
[10]	WANG Y N, YAUN B, NI X X. Subdivision technique of absolute angular encoder using array detector[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(2): 370-374.
[11]	齐荔荔, 万秋华. 图像式光电编码器的测角技术及其硬件实现[J]. 光学学报,2013,33(4):0412001. doi: 10.3788/AOS201333.0412001 QI L L, WAN Q H. Angle-measurement technology of an optical pattern rotary encoder and its hardware implementation[J]. Acta Optica Sinica, 2013, 33(4): 0412001. (in Chinese) doi: 10.3788/AOS201333.0412001
[12]	YU H, WAN Q H, LU X R, et al. Small-size, high-resolution angular displacement measurement technology based on an imaging detector[J]. Applied Optics, 2017, 56(3): 755-760. doi: 10.1364/AO.56.000755
[13]	YU H, WAN Q H, LU X R, et al. A robust sub-pixel subdivision algorithm for image-type angular displacement measurement[J]. Optics and Lasers in Engineering, 2018, 100: 234-238. doi: 10.1016/j.optlaseng.2017.09.006
[14]	于海, 万秋华, 赵长海, 等. 图像式光电编码器高分辨力细分算法及误差分析[J]. 光学学报,2017,37(3):0312001. doi: 10.3788/AOS201737.0312001 YU H, WAN Q H, ZHAO CH H, et al. A high-resolution subdivision algorithm for photographic encoders and its error analysis[J]. Acta Optica Sinica, 2017, 37(3): 0312001. (in Chinese) doi: 10.3788/AOS201737.0312001
[15]	赵长海, 万秋华, 孙莹. 光电轴角编码器的误码检测系统[J]. 电子测量与仪器学报,2012,26(5):463-468. ZHAO CH H, WAN Q H, SUN Y. Code error detection system for photoelectric shaft encoder[J]. Journal of Electronic Measurement and Instrument, 2012, 26(5): 463-468. (in Chinese)
[16]	于海, 万秋华, 梁立辉, 等. 光电编码器的动态误码检测系统[J]. 红外与激光工程,2016,45(9):0917001. doi: 10.3788/IRLA201645.0917001 YU H, WAN Q H, LIANG L H, et al. Dynamic code error detection system of photoelectric encoder[J]. Infrared and Laser Engineering, 2016, 45(9): 0917001. (in Chinese) doi: 10.3788/IRLA201645.0917001