Characteristic analysis for different beamsplitters of the plane holographic grating lithography system
-
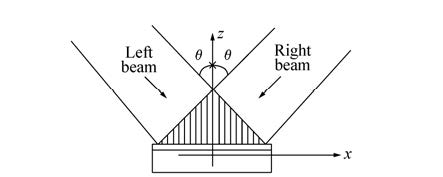
摘要: 分光器件是全息光栅曝光系统中的关键光学元件,它将入射激光光束分成两束,两相干光束叠加后形成干涉条纹。曝光系统的稳定性不但影响干涉条纹对比度,还影响光栅衍射波前像差、杂散光水平以及光栅掩模刻槽质量。为了提高曝光系统的稳定性,分析入射光束角度偏离与两相干光束夹角(2<em>θ</em>)的关系,并结合干涉条纹周期公式,分别导出了以光栅和棱镜作为分光器件时入射激光束角度偏离量与待制作光栅空间相位差的解析表达式,据此分析了光栅和棱镜曝光系统的稳定性。结果表明,采用光栅分光的曝光系统的稳定性比棱镜分光曝光系统稳定性提高5~6个数量级,这对长时间曝光制作全息光栅具有实际意义。Abstract: The beamsplitter has a critical role in the interference lithography, which splits one laser beam into two, therefore these two waves can interfere to produce the fringes. The instability of the interference lithography, which is determined by the selection of the beamsplitter, not only decreases the contrast of the patterns, but also causes the phase distortion, high scatter light and low quality of the groove. To improve the stability of the interference lithography system, based on the period equation of the fringes and the correction between deviation of the incidence and the interference beam angular variations(2<em>θ</em>), we discuss the phase distortion due to the alignment error of cube and the grating beamsplitter, and analyze the stability of the two different interference lithography system. Results indicate that in the grating manufacture, using the grating as the beamsplitter instead of the cube beamsplitter can increase the stability of lithography system by 5 to 6 orders of magnitude, which has a significant effect on grating fabrication with long-time exposure.
-
表 1 不同分光器件导致光栅空间相位差变化(以1 800 gr/mm为例)
Table 1. Phase distortion comparison between the cube and the grating beamsplitters for the same angle alignment error(1 800 gr/mm)
Grating area/mm Cube beamsplitter(n) Grating beamsplitter(n) 30° 45° 60° -
[1] [1] 孔鹏,巴音贺希格,李文昊,等.全息光栅非对称曝光显影的理论模拟及实时监测[J].光学学报,2010,30(1):65-69. KONG P, BAYANHESHIG, LI W H,et al.. Modeling and in-situ monitoring of the asymmetric exposure and development of holographic grating[J]. Acta Optica Sinica,2010,30(1):65-69.(in Chinese) [2] [2] 钱国林,李朝明,吴建宏,等.全息曝光条纹锁定系统特性研究[J].激光技术,2008,32(6):648-650. QIAN G L,LI CH M,WU J H,et al.. Study of characteristic of fringe locking system used to holographic exposure[J]. Laser Technology,2008,32(6):648-650.(in Chinese) [3] [3] SCHATTENBURG M L,CHEN C G. Progress towards a general grating patterning technology using phase-locked scanning beams[J]. SPIE,2002,4485:378-384. [4] [4] 祝绍箕.制作全息光栅的新装置[J].光学学报,1990,10(2):189-192. ZHU SH J. A new device for manufacturing holographic grating[J]. Acta Optica Sinica,1990,10(2):189-192.(in Chinese) [5] [5] 巴音贺希格,邵先秀,崔继承,等.制作平面全息光栅的离轴抛物镜/洛艾镜干涉系统[J].光学精密工程,2011,19(1):56-63. BAYANHESHIG,SHAO X X,CUI J CH,et al.. The off-axis parabolic/lioyd's mirror interferometric system for manufacturing plane holographic gratings[J]. Opt. Precision Eng.,2011,19(1):56-63.(in Chinese) [6] [6] HERSHEY R R,LEITH E N. Grating interferometers for producing large holographic gratings[J]. Applied Optics,1990,29(7):937-943. [7] [7] RUSHFORD M C,BRITTEN J A. Split-aperture laser pulse compressor design tolerant to alignment and line-density differences[J]. Optics Letters,2008,33(16):1902-1904. [8] [8] KONKOLA P,CHEN C G,Heilmann R,et al.. Beam steering system and spatial filtering applied to interference lithography[J]. J. Vac. Sci. Technol. B,2000,18(6):3282-3286. [9] [9] 徐福全,金陆,李文昊,等.曝光系统离焦对平面全息光栅衍射波前的影响[J].中国光学与应用光学,2008,1(1):57-61. XU F Q,JIN L,LI W H,et al.. Influence of defocus of exposure system on diffraction wavefront of plane holographic grating[J]. Chinese J. Optics and Applied Optics,2008,1(1):57-61.(in Chinese) [10] [10] 李朝明,吴建宏,陈欣荣,等.脉冲压缩光栅光学拼接方法研究[J].光学学报,2009,29(7):1943-1946. LI CH M,WU J H,CHEN X R,et al.. Research on the muti-exposure method to fabricate pulse compression masaicgrating[J]. Acta Optica Sinica,2009,29(7):1943-1946.(in Chinese) [11] [11] CHEN C G. Beam Alignment and image metrology for scanning beam interference lithography fabricating Gratings with namometer phase accuracy[D]. Boston:Massachusetts Institute of Technology,2003. [12] [12] ZHANG W,WU J H. New method for the fabrication of pulse compression grating[J]. SPIE,2006,6149:614921. [13] [13] 刘正坤,刘颖,邱克强,等.软X射线双频光栅设计及制作[J].光学精密工程,2013,21(7):1780-1785. LIU ZH K,LIU Y,QIU K Q,et al.. Design and fabrication of soft X-ray double frequency grating[J]. Opt. Precision Eng.,2013,21(7):1780-1785.(in Chinese). -






 下载:
下载: