Measurement of the location of projectile burst on water surface by dynamic image method and its error analysis
-
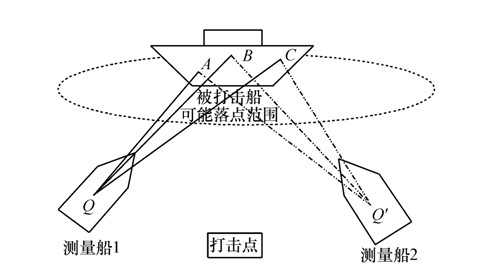
摘要: 为了测量弹丸水面落点的位置, 建立了基于CCD相机动态像面的测量模型。该模型通过CCD相机辅助采集相关点位的图像信息, 对水面落点的位置函数以及误差进行了研究。首先, 利用空间几何获得靶船上三定点相对于测量船的方位、俯仰信息。接着, 结合t时刻观测图像上定点的像面坐标, 运用底片常数模型建立像面坐标和角度信息两套参量之间的关系函数, 从而得到目标落点的方位、俯仰信息, 再利用异面交会法计算出目标落点位置。最后, 分析了目标落点位置的误差来源(质心误差, 位置误差)、误差以及各误差源与位置坐标之间的关系。实验结果表明:在测量船位置精度达到0.05 m, 图像质心定位精度达到0.5 pixel时, 在最小交会误差的情况下, 目标落点的位置测量误差分别为2.8, 4.9, 4.3 m。Abstract: In order to measure the value of projectile points on the water surface accurately, a model of dynamic images measurement based on CCD camera is established. The function of the value of the surface point and its measuring error are analyzed by using the collected images information of the relative points taken by CCD camera secondarily. First, with the knowledge of spatial geometry, the azimuth and the elevation angles of three designated points on the target ship relative to the measuring ship are obtained. Then, combined with image coordinates of the specified points at t point, the relationship function of two sets of parameters between the image plane coordinate and angle information is presented by taking the constant model, so the azimuth and the elevation angles information of the projectile point is obtained. The function of three-dimensional projectile burst coordinates is presented by non-coplane intersection method. Finally, the coordinate's errors from the evaluation of the pinpoint of the image and the location measurement accuracy are discussed and the relationship is investigated. Experimental results indicate that the three-dimensional projectile burst coordinate's measuring error are 2.8, 4.9, 4.3 m, respectively, in the condition of the minimum intersection error, when the position accuracy is up to 0.05 m and the image pinpoint accuracy to be able to 0.5 pixel.
-
图 1 水面整体测量示意图
Figure 1. Schematic diagram of overall measuring system of water surface
图 2 角度坐标和图像坐标的几何关系
Figure 2. Geometrical relationship between angular coordinates and image coordinates
图 3 测量船Q拍摄的t时刻实际图像
Figure 3. Image of the projectile point obtained from measuring ship Q(t time)
表 1 靶标船上定点以及测量船的地心坐标
Table 1. Geocentric coordinates of points and measuring ships
No. x/m y/m z/m A -2 481 438.920 4 172 027.248 4 123 447.395 B -2 481 451.865 4 172 019.178 4 123 447.768 C -2 481 464.340 4 172 011.337 4 123 448.191 Q -2 479 586.645 4 176 130.661 4 120 427.098 Q′ -2 485 831.796 4 172 054.275 4 120 791.172 
下载: 导出CSV
表 2 定点和目标点的像元位置坐标
Table 2. Image coordinates of specified points and projectile point
No. 测量船Q 测量船Q′ 横坐标 纵坐标 横坐标 纵坐标 x/pixel y/pixel x′/pixel y′/pixel A -25.4 3 -23.9 0 B 2 3 1.5 0 C 28.3 3 26.3 0 M -10.8 3 83.1 0
下载: 导出CSV
表 3 靶水面落点坐标和相应方向上的误差
Table 3. Result of value of the projectile point and its error
真值/m 误差/m x -2 481 459.4 2.8 y 4 171 993.0 4.9 z 4 123 469.6 4.3
下载: 导出CSV
-
[1] [2] [3] [4] [5] [6] [7] [8] [9] [109] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] -
下载:
计量
- 文章访问数: 1547
- HTML全文浏览量: 511
- PDF下载量: 620
- 被引次数: 0
