Analysis of multi-factor influences of tilt-to-length coupling noise in a test mass interferometer
doi: 10.37188/CO.EN-2024-0031
-
摘要:
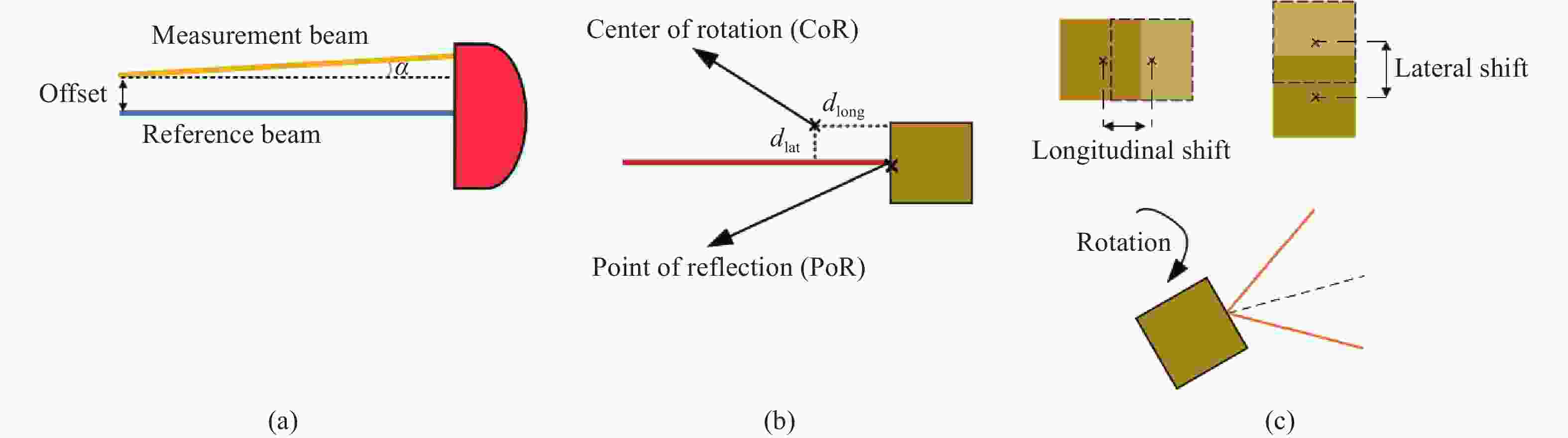
在基于外差干涉原理的空间引力波探测任务中,抖动光程耦合噪声是一个重要的光学噪声源,对测量系统的精度具有显著影响。本文提出了一种多因素共同作用下抖动光程耦合噪声分析的方法。首先,设计了一个等效的测试质量干涉仪仿真光学平台,并采用高斯光束追踪模拟光束传播。通过模拟干涉信号,可以分析各种因素对抖动光程耦合噪声的影响,包括位置因素、光束参数因素、探测器参数因素和信号定义因素。在此基础上,在满足分析要求的参数范围内,构建了由多个影响因素组成的随机参数空间,并通过基于方差的全局敏感性分析对随机采样得到的模拟结果进行评估。主要效应指数和总效应指数的计算结果表明,测试质量的旋转角度和活塞效应(径向)对测试质量干涉仪中的抖动光程耦合噪声有显著影响。这一结论为空间激光干涉测量系统的设计和优化提供了定性参考。
Abstract:For space-borne gravitational wave detection missions based on the heterodyne interferometry principle, tilt-to-length (TTL) coupling noise is an important optical noise source, significantly influencing the accuracy of the measurement system. We present a method for analyzing TTL coupling noise under the joint influence of multiple factors. An equivalent simulated optical bench for the test mass interferometer was designed, and Gaussian beam tracing was adopted to simulate beam propagation. By simulating the interference signal, it can analyze the impact of various factors on the TTL coupling noise, including positional, beam parameters, detector parameters, and signal definition factors. On this basis, a random parameter space composed of multiple influential factors was constructed within a range satisfying the analysis requirement, and the corresponding simulation results from random sampling were evaluated via variance-based global sensitivity analysis. The calculated results of the main and total effect indexes show that the test mass rotation angle and the piston effect (lateral) significantly influence the TTL coupling noise in the test mass interferometer. The analysis provides a qualitative reference for designing and optimizing space-borne laser interferometry systems.
-
Key words:
- space interferometry /
- optical simulation /
- tilt-to-length coupling noise
-
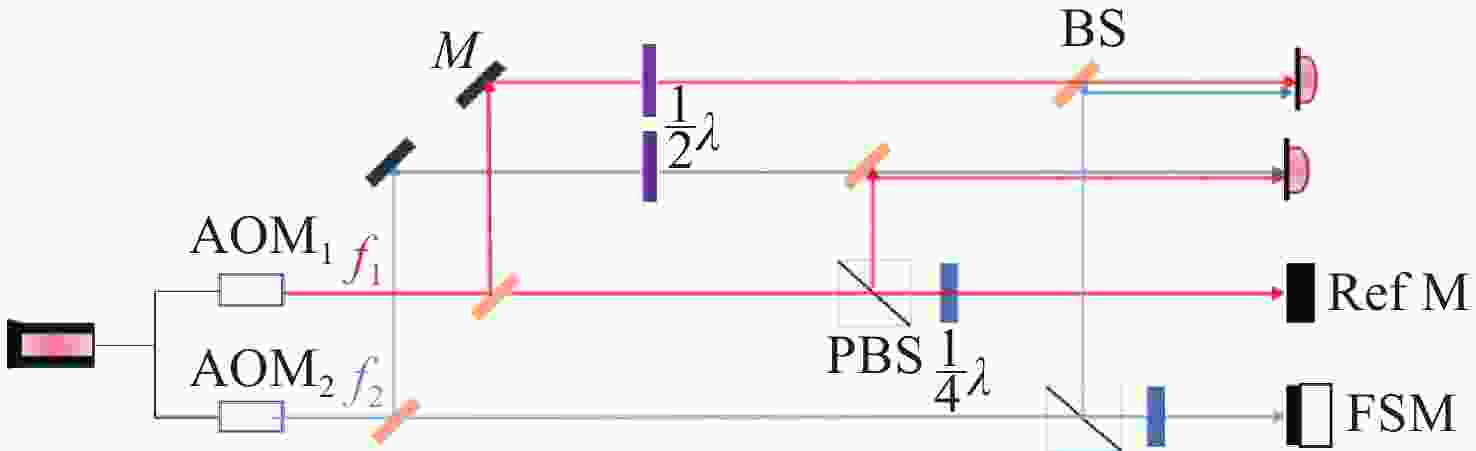
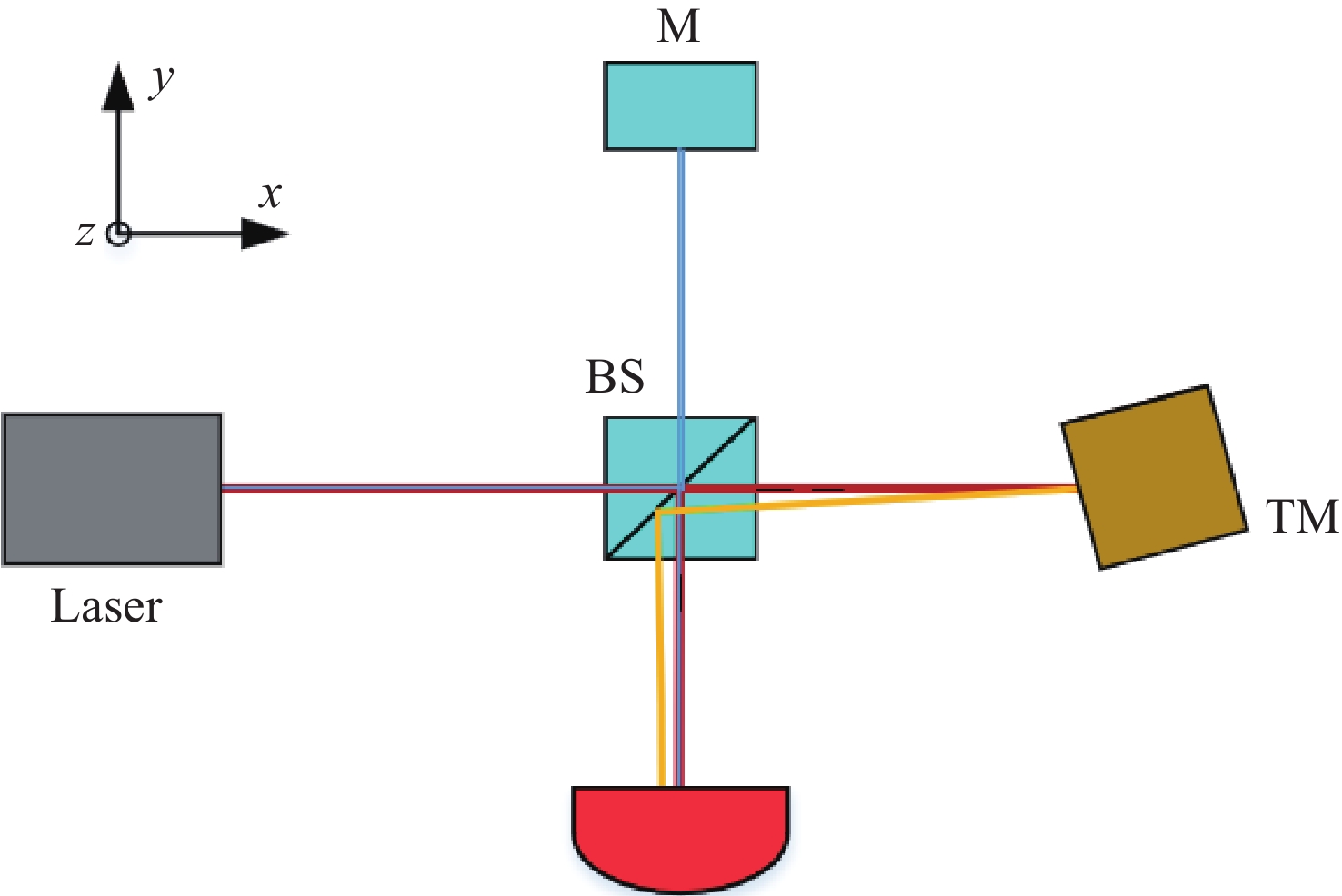
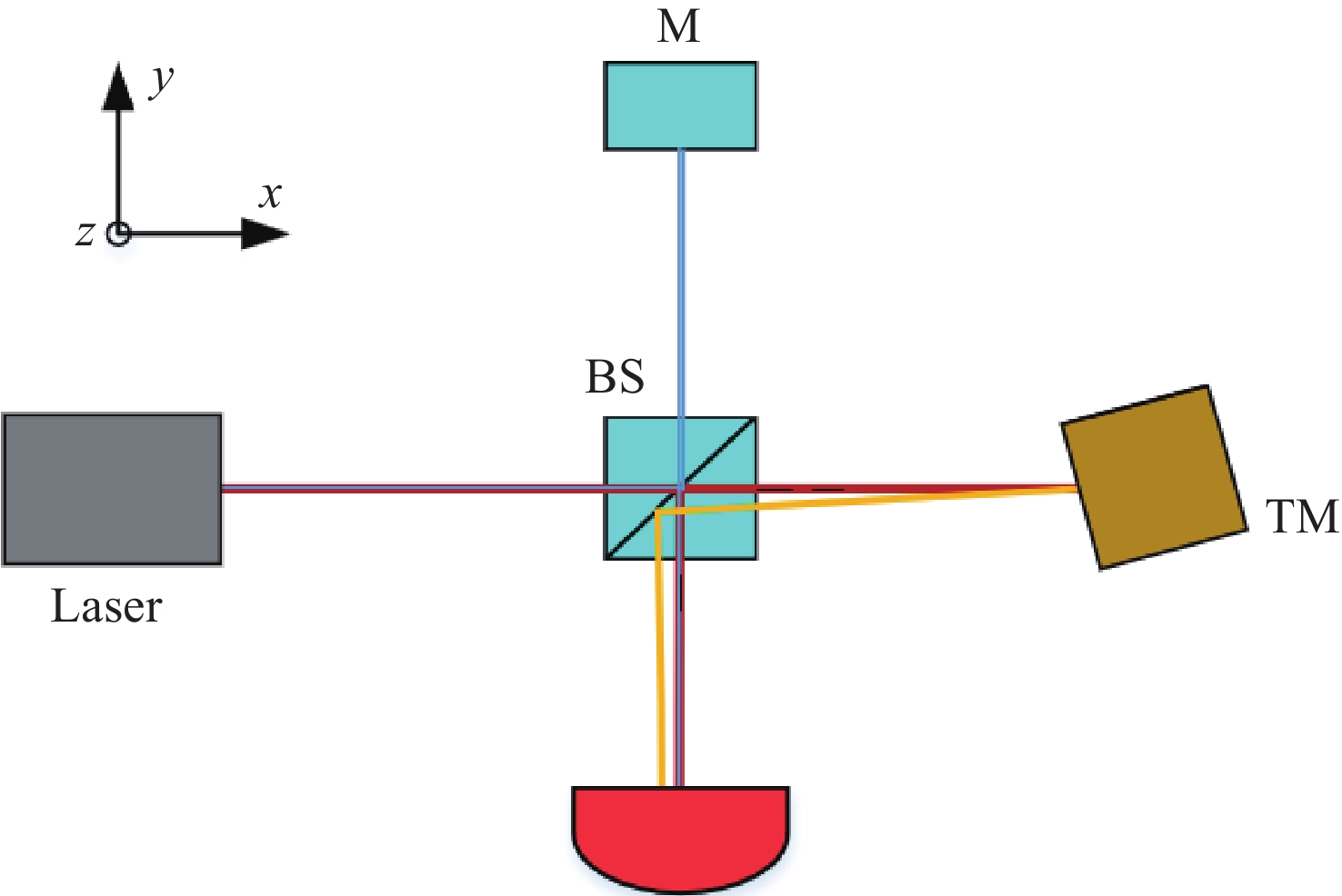
Table 1. The type, position, and orientation of each component in the simulated optical bench used to analyze TTL coupling
Label Component Name Center coordinate
cmNormal Vector Laser Laser (0,0,0) (1,0,0) BS Beam splitter (25,0,0) (−1,0,0) M Mirror (25,50,0) (0,−1,0) TM Test mass (50,0,0) (1,0,0) QPD Quadrant photodiode (25,-25,0) (0,1,0) Table 2. Physical parameters list
Parameter description Value Reference beam waist 0.5 mm Distance from reference beam waist 0 Reference beam frequency 2.8195 ×108 MHz +120 MHzMeasurement beam waist 0.5 mm Distance from measurement beam waist 0 mm Measurement beam frequency 2.8195 ×108 MHz +
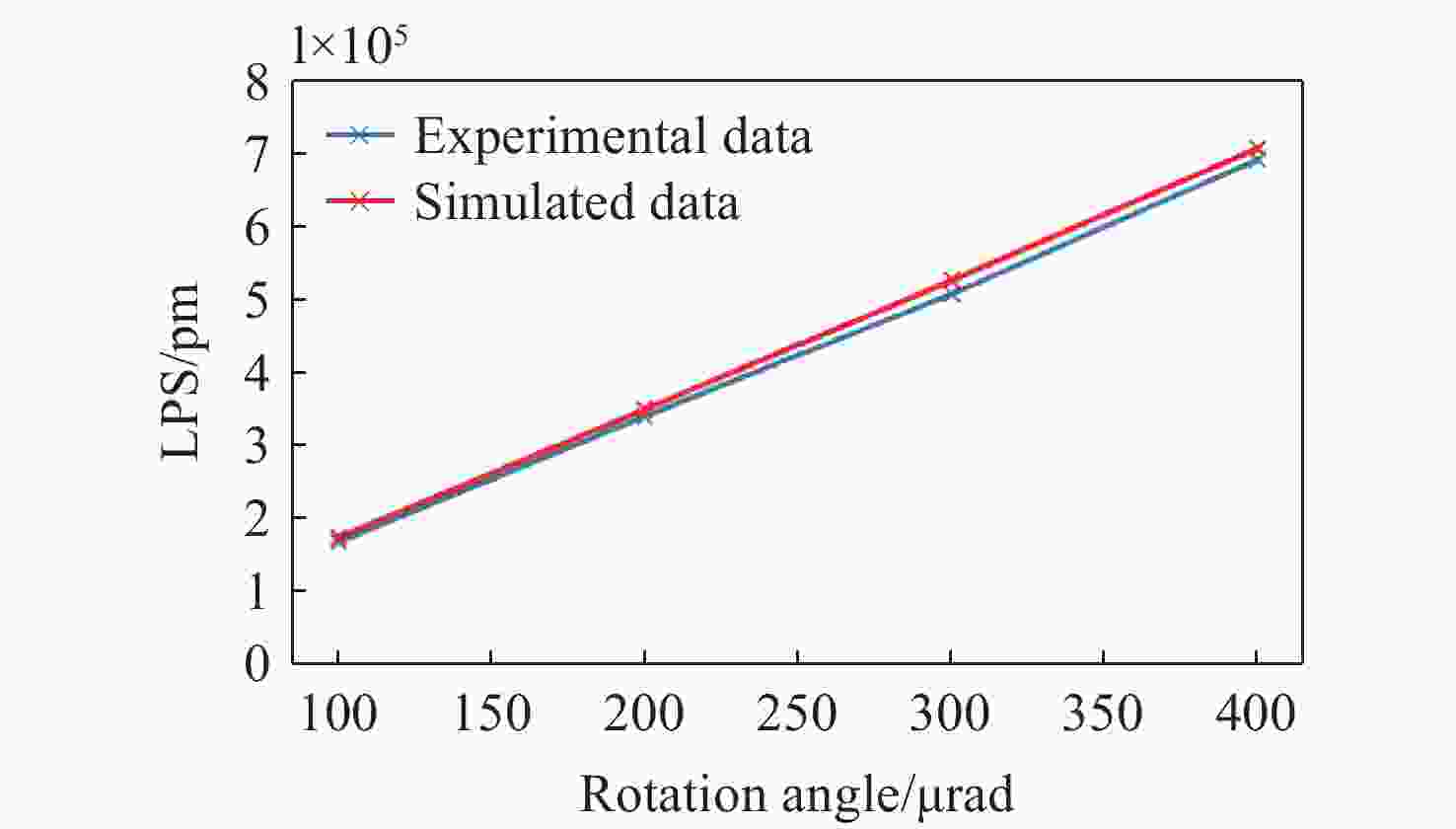
120 MHz+1.6 MHzQPD radius 1 cm QPD slit size 50 µm Table 3. Comparison of rotation angle (µrad) and relative error (%)
Rotation angle (µrad) Relative error (%) 100 3.78 200 2.84 300 3.69 400 2.24 Table 4. Parameter space for multiple factor analysis
Factors Parameter Range Positional Beam offset (0 μm, 100 μm) Piston effect (lateral) (0 mm, 1 mm) Piston effect (longitudinal) (0 mm, 1 mm) Test mass lateral shift (0 μm, 100 μm) Test mass longitudinal shift (0 μm, 100 μm) Rotation angle (0 μrad, 100 μrad) Beam
parameterMeasurement beam waist (0.5mm, 1 mm) The distance from the waist
of the measurement beam(0 mm, 50 mm) Detector
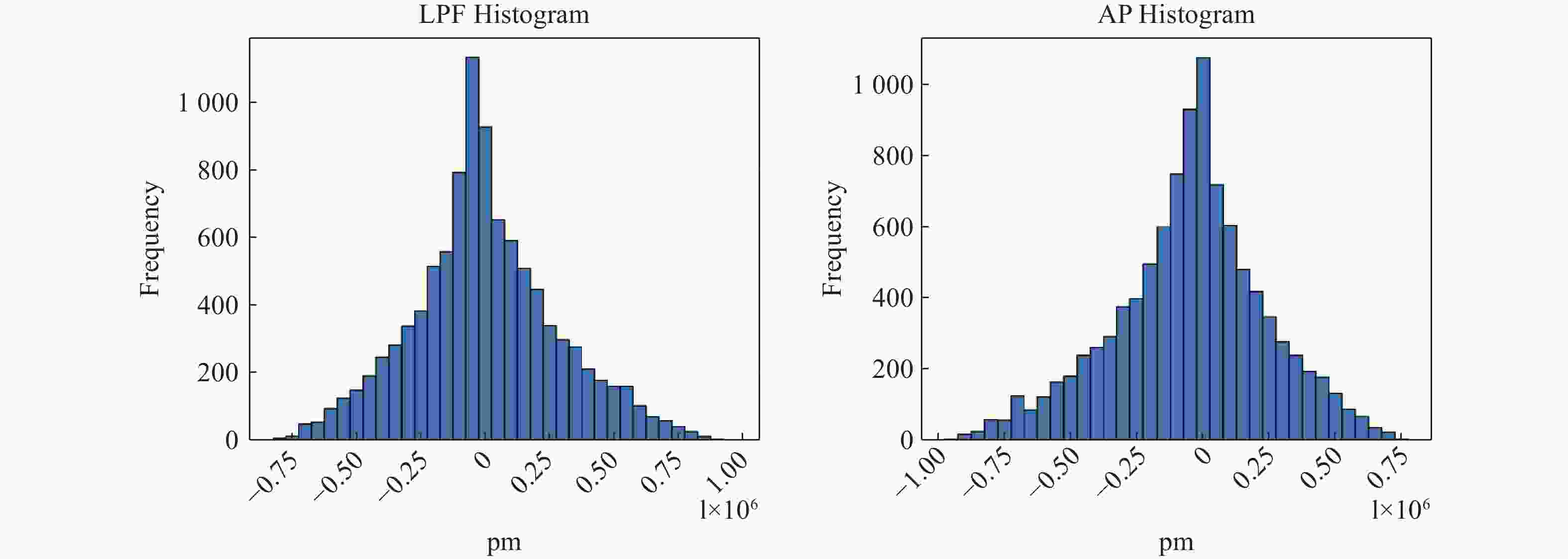
parameterQPD slit (0 μm, 100 μm) Table 5. Maximum (absolute value) and minimum (absolute value) of the LPS with both LPF and AP in 10,000 simulations
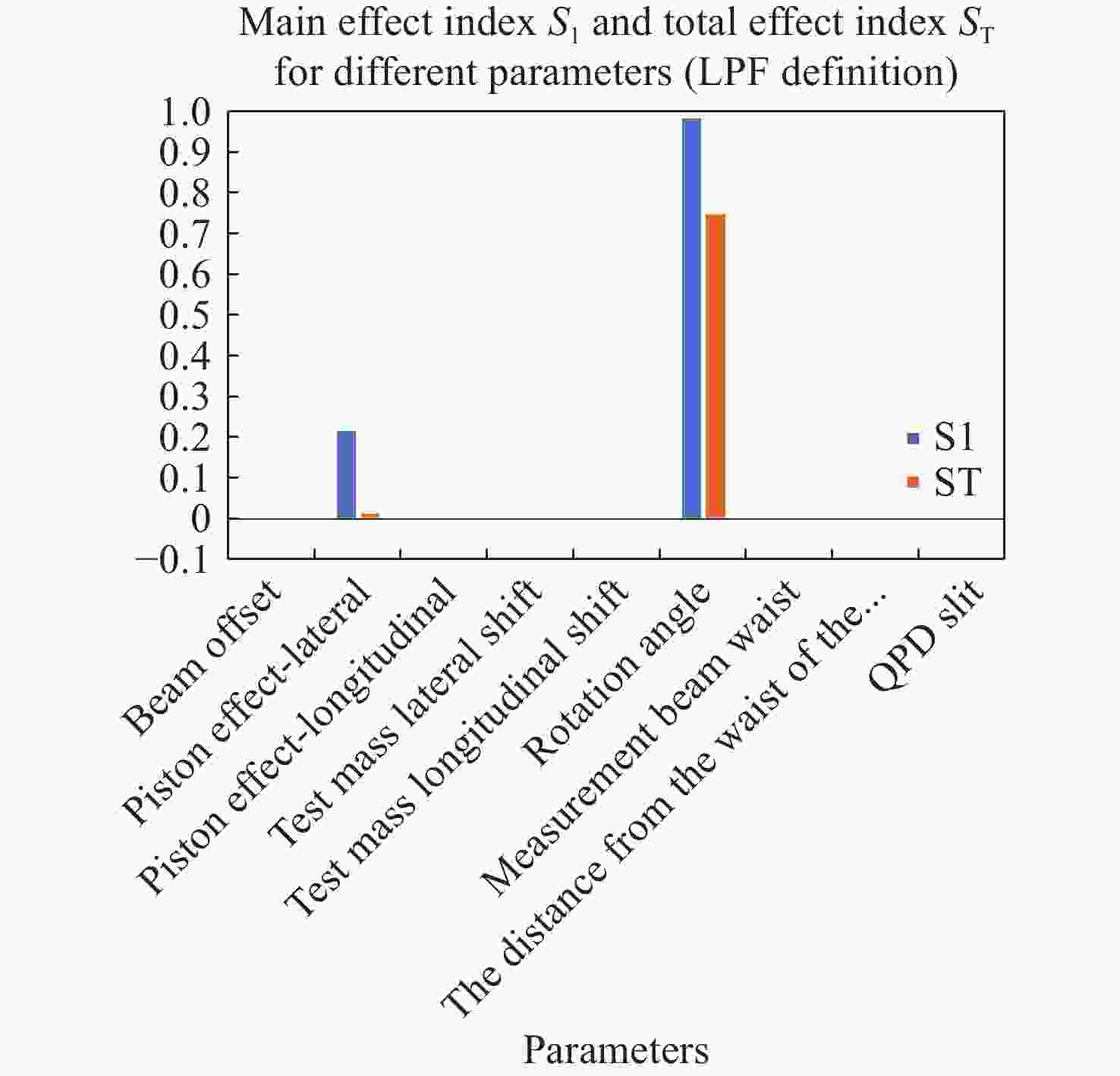
Signal definition Maximum Minimum LPF 9.6939 ×105 pm6.4400 pmAP 9.1285 ×105 pm14.7801 pmTable 6. Main effect index S1 and total effect index ST for different parameters (LPF definition)
Factors Parameter S1 ST Positional Beam offset 0.00037 0.00023 Piston effect (lateral) 0.01516 0.21815 Piston effect (longitudinal) 8.8911 ×10−75.3478 ×10−9Test mass lateral shift − 0.00096 0.00217 Test mass longitudinal shift − 1.0968 ×10−75.9016 ×10-11Rotation angle 0.75350 0.99122 Beam
parameterMeasurement beam waist 0.00081 0.00240 Distance from the
measurement beam’s waist5.8822 ×10−63.1740 ×10−7Detector
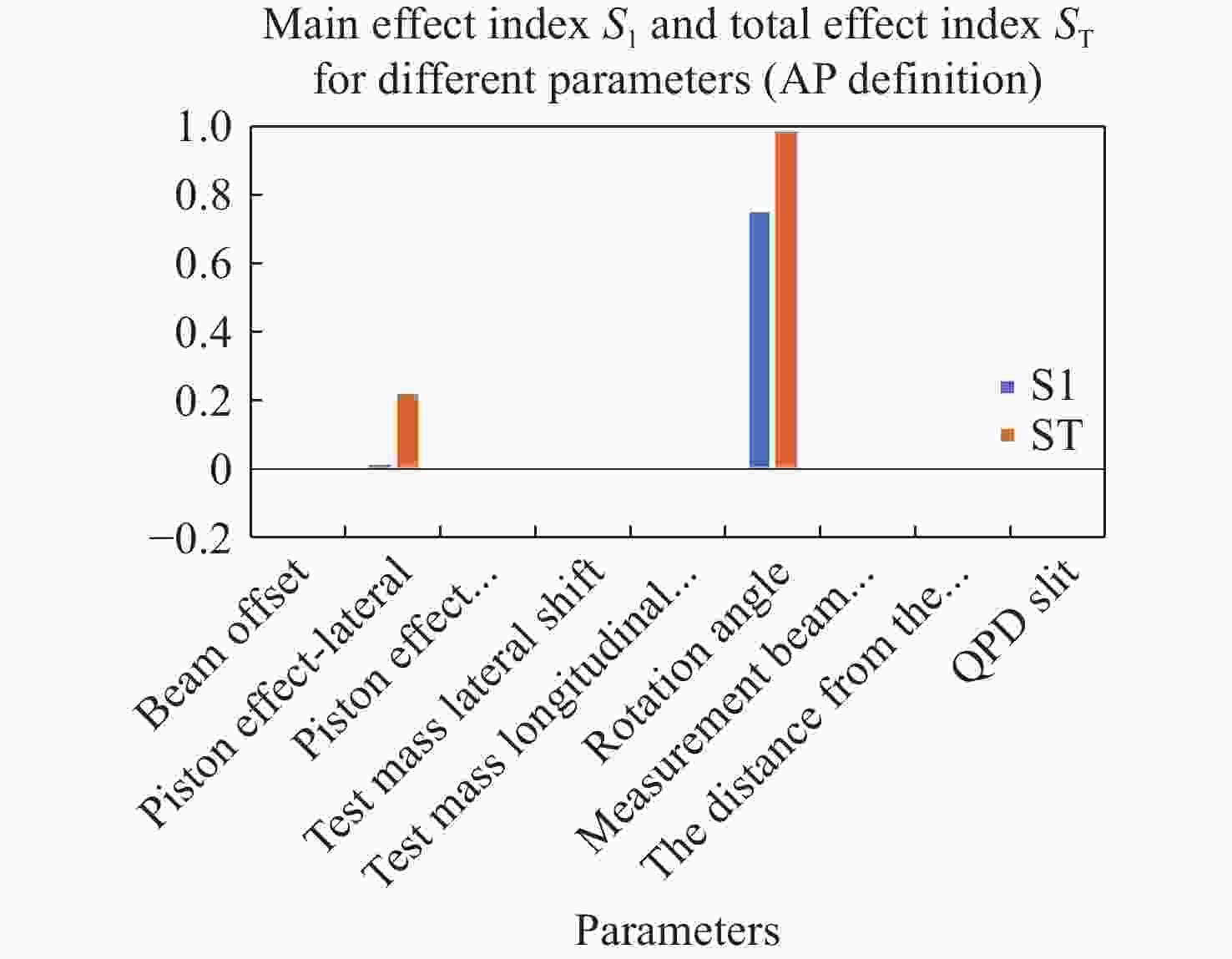
parameterQPD slit 0.00017 0.00028 Table 7. Main effect index S1 and total effect index ST for different parameters (AP definition)
Factors Parameter S1 ST Positional Beam offset 0.00093 0.00047 Piston effect (lateral) 0.01409 0.21586 Piston effect (longitudinal) 1.6607 ×10−65.29173 ×10−9Test mass lateral shift - 0.00117 0.00214 Test mass longitudinal shift − 1.6703 ×10−77.6198 ×10-11Rotation angle 0.75988 0.99156 Beam
parameterMeasurement beam waist 0.00085 0.00039 Distance from the
measurement beam’s waist2.1826 ×10−65.2593 ×10−8Detector
parameterQPD slit 0.00073 0.00035 -
[1] AMARO-SEOANE P, AUDLEY H, BABAK S, et al. Laser interferometer space antenna[J]. arXiv preprint arXiv: 1702.00786, 2017. [2] LUO Z R, ZHANG M, JIN G, et al. Introduction of Chinese space-borne gravitational wave detection program “Taiji” and “Taiji-1” satellite mission[J]. Journal of Deep Space Exploration, 2020, 7(1): 3-10. [3] LUO J, CHEN L SH, DUAN H Z, et al. TianQin: a space-borne gravitational wave detector[J]. Classical and Quantum Gravity, 2016, 33(3): 035010. doi: 10.1088/0264-9381/33/3/035010 [4] OTTO M. Time-delay interferometry simulations for the laser interferometer space antenna[D]. Hannover: Gottfried Wilhelm Leibniz Universität Hannover, 2015. [5] SCHUSTER S, WANNER G, TRÖBS M, et al. Vanishing tilt-to-length coupling for a singular case in two-beam laser interferometers with Gaussian beams[J]. Applied Optics, 2015, 54(5): 1010-1014. doi: 10.1364/AO.54.001010 [6] WANG L Y, LI Y Q, CAI R. Noise suppression of tilt-to-length coupling in space laser interferometer[J]. Optics and Precision Engineering, 2021, 29(7): 1491-1498. (in Chinese). doi: 10.37188/OPE.20212907.1491 [7] CHWALLA M, DANZMANN K, BARRANCO G F, et al. Design and construction of an optical test bed for LISA imaging systems and tilt-to-length coupling[J]. Classical and Quantum Gravity, 2016, 33(24): 245015. doi: 10.1088/0264-9381/33/24/245015 [8] SCHUSTER S. Tilt-to-length coupling and diffraction aspects in satellite interferometry[D]. Hannover: Gottfried Wilhelm Leibniz Universität Hannover, 2017. [9] HARTIG M S, SCHUSTER S, WANNER G. Geometric tilt-to-length coupling in precision interferometry: mechanisms and analytical descriptions[J]. Journal of Optics, 2022, 24(6): 065601. doi: 10.1088/2040-8986/ac675e [10] HARTIG M S, SCHUSTER S, HEINZEL G, et al. Non-geometric tilt-to-length coupling in precision interferometry: mechanisms and analytical descriptions[J]. Journal of Optics, 2023, 25(5): 055601. doi: 10.1088/2040-8986/acc3ac [11] ZHAO Y, WANG ZH, LI Y P, et al. Method to remove tilt-to-length coupling caused by interference of flat-top beam and Gaussian beam[J]. Applied Sciences, 2019, 9(19): 4112. doi: 10.3390/app9194112 [12] WANNER G, SCHUSTER S, TRÖBS M, et al. A brief comparison of optical pathlength difference and various definitions for the interferometric phase[J]. Journal of Physics: Conference Series, 2015, 610: 012043. doi: 10.1088/1742-6596/610/1/012043 [13] SASSO C P, MANA G, MOTTINI S. Coupling of wavefront errors and pointing jitter in the LISA interferometer: misalignment of the interfering wavefronts[J]. Classical and Quantum Gravity, 2018, 35(24): 245002. doi: 10.1088/1361-6382/aaea0f [14] ZHAO Y, SHEN J, FANG CH, et al. Tilt-to-length noise coupled by wavefront errors in the interfering beams for the space measurement of gravitational waves[J]. Optics Express, 2020, 28(17): 25545-25561. doi: 10.1364/OE.397097 [15] ZHAO Y, SHEN J, FANG CH, et al. Far-field optical path noise coupled with the pointing jitter in the space measurement of gravitational waves[J]. Applied Optics, 2021, 60(2): 438-444. doi: 10.1364/AO.405467 [16] LI J C, LIN H A, LUO J X, et al. Optical design of space gravitational wave detection telescope[J]. Chinese Optics, 2022, 15(4): 761-769. (in Chinese). doi: 10.37188/CO.2022-0018 [17] SCHUSTER S, TRÖBS M, WANNER G, et al. Experimental demonstration of reduced tilt-to-length coupling by a two-lens imaging system[J]. Optics Express, 2016, 24(10): 10466-10475. doi: 10.1364/OE.24.010466 [18] WEAVER A J. Investigating limits on gravitational wave detection by laser interferometry using hermite-gauss mode representations of paraxial light propagation[D]. Gainesville: University of Florida, 2021. [19] PACZKOWSKI S, GIUSTERI R, HEWITSON M, et al. Postprocessing subtraction of tilt-to-length noise in LISA[J]. Physical Review D, 2022, 106(4): 042005. doi: 10.1103/PhysRevD.106.042005 [20] HOUBA N, DELCHAMBRE S, ZIEGLER T, et al. Optimal estimation of tilt-to-length noise for spaceborne gravitational-wave observatories[J]. Journal of Guidance, Control, and Dynamics, 2022, 45(6): 1078-1092. doi: 10.2514/1.G006064 [21] GEORGE D, SANJUAN J, FULDA P, et al. Calculating the precision of tilt-to-length coupling estimation and noise subtraction in LISA using Fisher information[J]. Physical Review D, 2023, 107(2): 022005. doi: 10.1103/PhysRevD.107.022005 [22] ZHAO M Y, PENG X D, YANG ZH, et al. Preliminary simulation of intersatellite laser interference link for the Taiji program[J]. Journal of Astronomical Telescopes, 2022, 8(3): 038002. [23] SOBOL’ I M. On sensitivity estimation for nonlinear mathematical models[J]. Matematicheskoe Modelirovanie, 1990, 2(1): 112-118. [24] HOMMA T, SALTELLI A. Importance measures in global sensitivity analysis of nonlinear models[J]. Reliability Engineering & System Safety, 1996, 52(1): 1-17. [25] SOBOL’ I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1-3): 271-280. doi: 10.1016/S0378-4754(00)00270-6 [26] SALTELLI A, ANNONI P, AZZINI I, et al. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index[J]. Computer Physics Communications, 2010, 181(2): 259-270. doi: 10.1016/j.cpc.2009.09.018 -





 下载:
下载: