模式能量梯度上升的光束入腔指向方法

邢成文; 徐天尧; 马超群; 栾苏琪; 李跃; 孟范超; 孟令强; 吕刚; 印雄飞; 贾建军

doi:10.37188/CO.2025-0053

模式能量梯度上升的光束入腔指向方法

doi: 10.37188/CO.2025-0053

cstr: 32171.14.CO.2025-0053

邢成文^{1, 3,},
徐天尧¹,
马超群¹,
栾苏琪¹,
李跃¹,
孟范超^{1, 2},
孟令强¹,
吕刚²,
印雄飞^1, ,,
贾建军^{1, 2, 4, ,}

1.
国科大杭州高等研究院物理与光电工程学院, 浙江杭州 310024
2.
中国科学院上海技术物理研究所空间主动光电技术重点实验室, 上海 200083
3.
中国科学院上海光学精密机械研究所, 上海 201800
4.
中国科学院大学, 北京 100049

基金项目: 国家重点研发计划（No. 2024YFC2206900，No. 2021YFC2201804）

详细信息

作者简介:
邢成文（1996—），男，安徽阜阳人，博士研究生，主要研究领域为激光技术。E-mail：xingchengwen21@mails.ucas.ac.cn

印雄飞（1973—），男，江苏泰兴人，博士，教授，2000年于上海交通大学获得博士学位。主要研究方向为激光精密测量与加工。E-mail：yinxiongfei@ucas.ac.cn

贾建军（1972—），男，山西永济人，博士，研究员，1999年于上海交通大学获得博士学位，主要研究领域为空间光电技术。E-mail：jjjun10@mail.sitp.ac.cn

中图分类号: O43
计量
- 文章访问数: 84
- HTML全文浏览量: 40
- PDF下载量: 10
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-15
- 修回日期: 2024-04-14
- 网络出版日期: 2025-04-29

Cavity alignment method based on mode energy gradient ascent

XING Cheng-wen^{1, 3
,},
XU Tian-yao¹,
MA Chao-qun¹,
LUAN Su-qi¹,
LI Yue¹,
MENG Fan-chao^{1, 2},
MENG Ling-qiang¹,
LV Gang²,
YIN Xiong-fei^{1
, ,},
JIA Jian-jun^{1, 2, 4
, ,}

1.
School of Physics and Optoelectrical Engineering, Hangzhou Institute for Advanced Study, University of Chinese Academy of Sciences, Hangzhou 310024, China
2.
Key Laboratory of Space Active Opto-Electronics Technology, Shanghai Institute of Technical Physics, Chinese Academy of Sciences, Shanghai 200083, China
3.
Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai 201800, China
4.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: Supported by National Key R & D Program of China (No. 2024YFC2206900, No. 2021YFC2201804)

More Information

Corresponding author: yinxiongfei@ucas.ac.cn; jjjun10@mail.sitp.ac.cn

摘要

摘要:
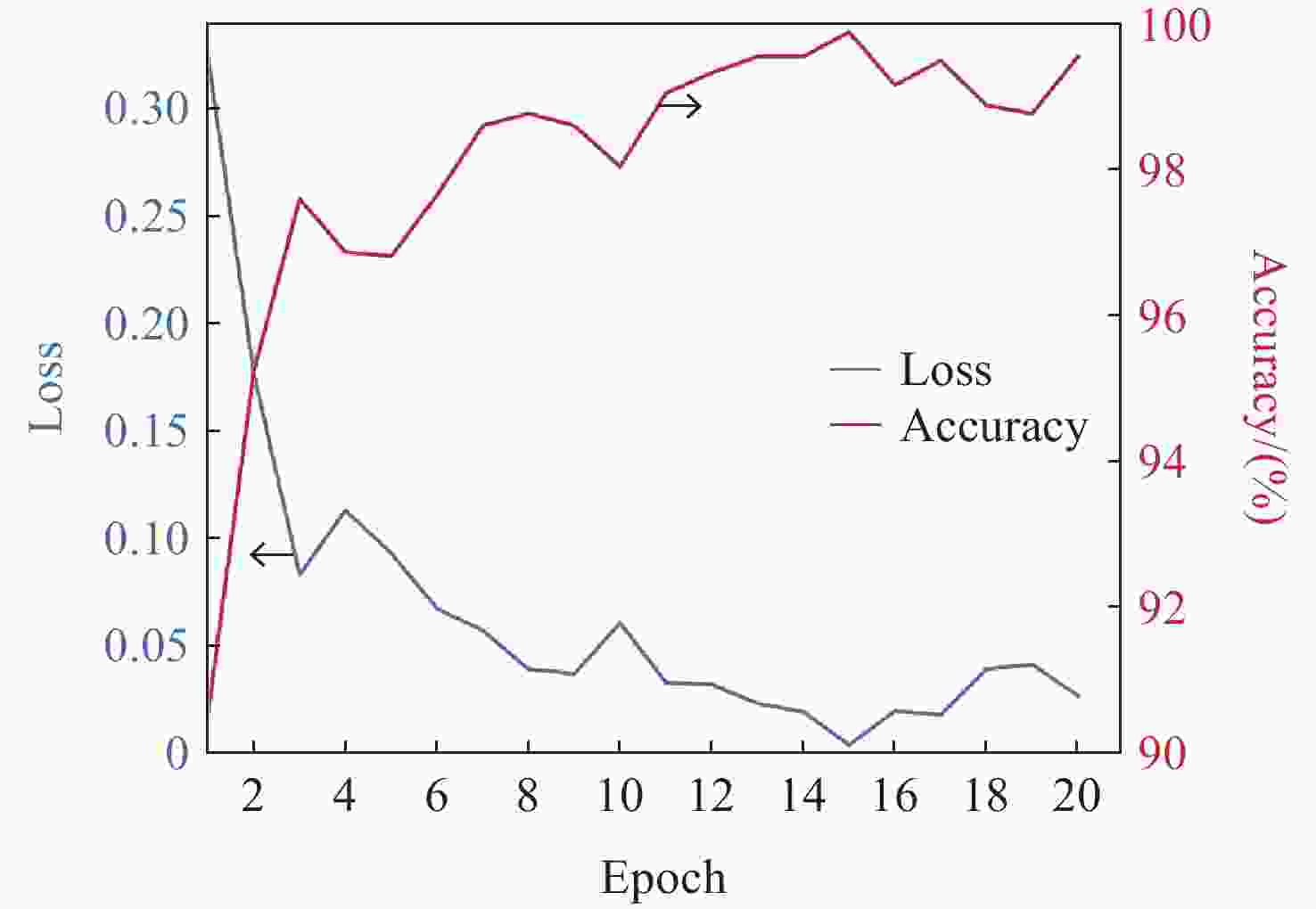
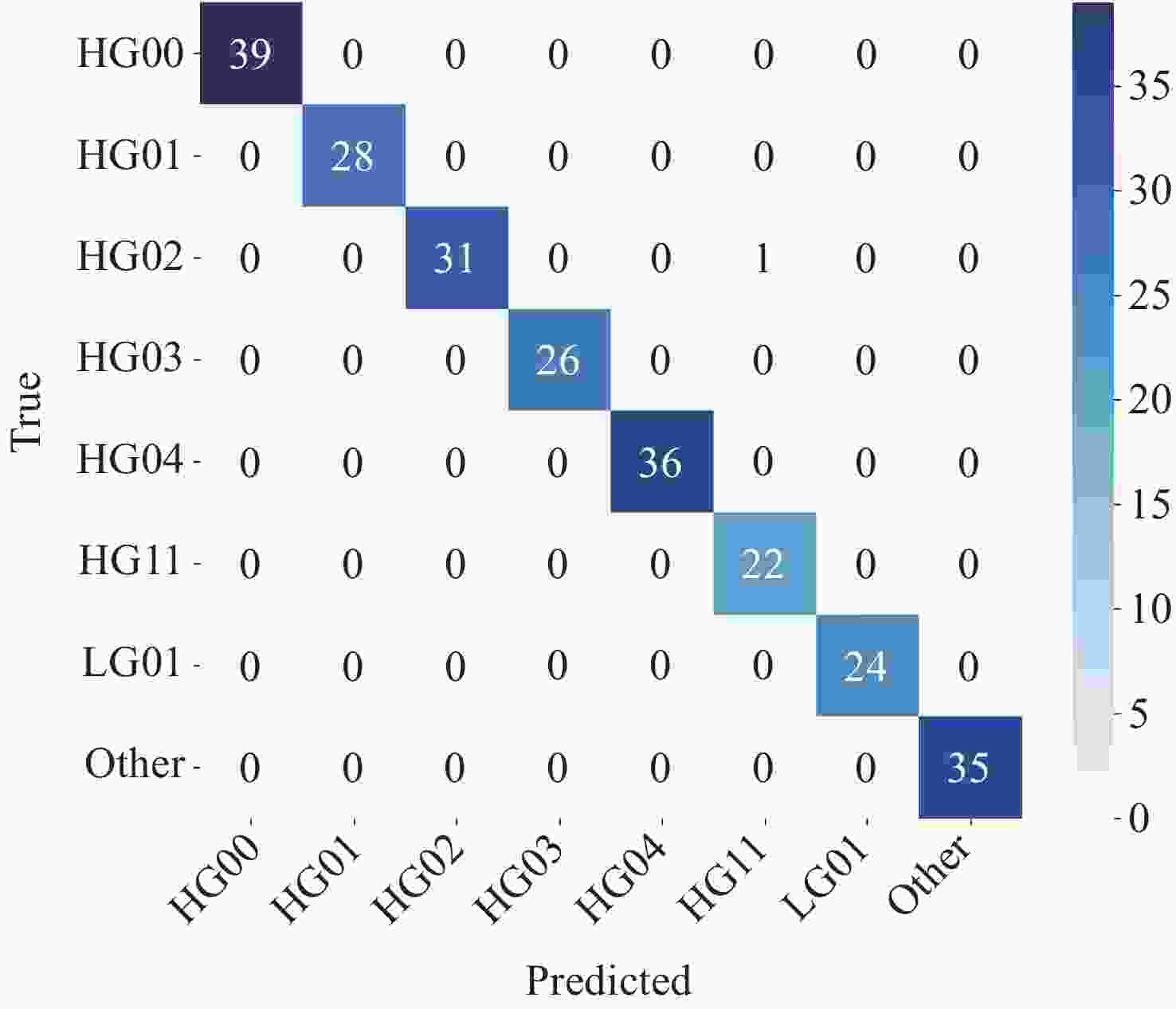
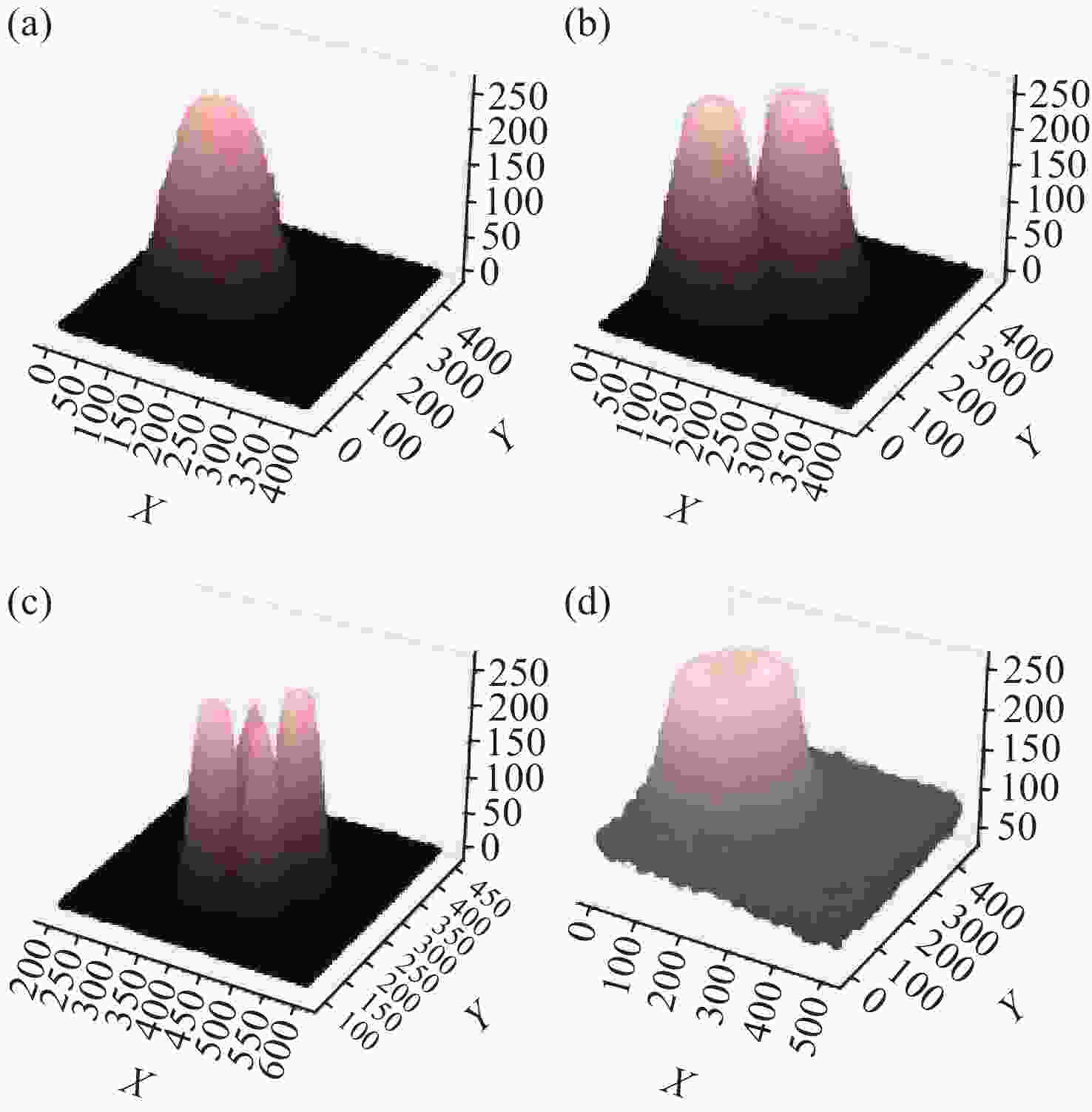
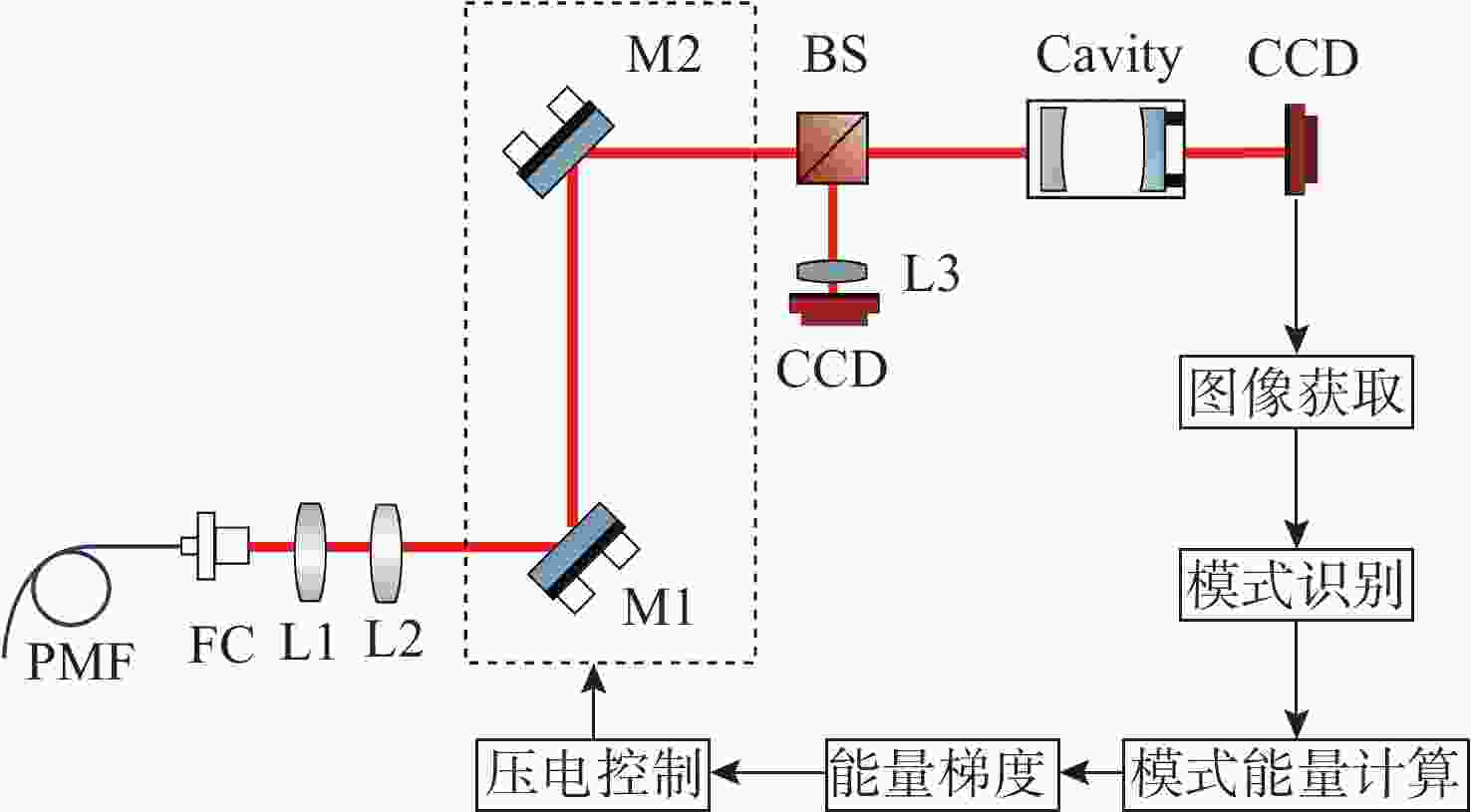
为了解决光束与法布里珀罗腔的入腔失调问题，本文基于谐振模式能量梯度上升自适应调整双反射镜步进，实现所需谐振模式的入腔光束指向。首先，利用双反射镜步进与入腔光束失调的关系，提出分离式入腔光束平移与角度调整方法。其次，利用EfficientNET神经网络对谐振模式图片进行分类，实现不同激光模式的图像识别。最后，利用腔后模式能量梯度调整双反射镜步进，低成本、高效率实现目标谐振模式的入腔耦合。本文的入腔光束指向调整方法为超稳激光器以及引力波探测中法布里珀罗腔的入腔耦合提供了新思路。
- 入腔耦合 /
- 光束指向控制 /
- 法布里珀罗腔 /
- 双快速反射镜 /
- 梯度上升
Abstract:
Addressing the issue of beam alignment with Fabry-Pérot cavities, this paper proposes an adaptive dual-mirror step adjustment method based on the gradient ascent of transmitted resonant mode energy to achieve cavity coupling. First, leveraging the relationship between the reflection angles of the dual mirrors and the beam pointing, independent adjustment of the incident beam position and angle was proposed. Second, the EfficientNet neural network was used to classify resonant mode images, enabling identification of different mode images. Third, the energy gradient of the cavity mode was utilized for adaptively dual mirrors step adjustment, enabling low-cost and efficient cavity coupling of both fundamental and higher-order modes. The beam pointing adjustment method proposed will offer a novel solution for coupling lasers with Fabry-Pérot cavities in ultra-stable lasers and gravitational wave detection.
- cavity coupling /
- beam pointing /
- Fabry-Pérot cavities /
- dual steering mirrors /
- gradient ascent

HTML全文

图 1 光束入腔失调引起的模式能量分布

Figure 1. Mode energy distribution induced by beam misalignment

下载: 全尺寸图片幻灯片

图 2 不同阶模式的对数能量与失调量的关系

Figure 2. Relationship between logarithmic energy of optical modes and misalignment

下载: 全尺寸图片幻灯片

图 3 梯度上升法求解第n阶模式能量的极值点

Figure 3. Finding the maximum of n-th order mode energy utilizing gradient ascent method

下载: 全尺寸图片幻灯片

图 4 双反射镜系统角度组合方案。 (a)平移; (b)旋转

Figure 4. Angle combination strategies for dual-mirror systems. (a) Lateral offset; (b) tilt

下载: 全尺寸图片幻灯片

图 5 谐振模式数据采集装置

Figure 5. Resonant mode data acquisition device

下载: 全尺寸图片幻灯片

图 6 谐振模式数据集示例

Figure 6. Examples of the resonant mode dataset

下载: 全尺寸图片幻灯片

图 7 利用EfficientNet在数据集上训练的准确度和损失曲线

Figure 7. Accuracy and loss curves of training on the dataset using EfficientNet

下载: 全尺寸图片幻灯片

图 8 利用EfficientNet在测试集上模式图片识别的混淆矩阵

Figure 8. Confusion matrix of the mode picture recognition on the test dataset by EfficientNet

下载: 全尺寸图片幻灯片

图 9 不同模式的强度图。(a) HG00模式；(b) HG01模式；(c) HG02模式；(d) LG01模式

Figure 9. Intensity maps under different modes. (a) HG00; (b) HG01; (c) HG02; (d) LG01

下载: 全尺寸图片幻灯片

图 10 实验装置框图

Figure 10. Block diagram of the experimental set-up

下载: 全尺寸图片幻灯片

图 11 实验装置图

Figure 11. Experimental set-up

下载: 全尺寸图片幻灯片

图 12 基模强度对数值与调整角度的关系

Figure 12. Relationship between the tilt angles and logarithmic intensity of the fundamental mode

下载: 全尺寸图片幻灯片

图 13 基于梯度上升的入腔调整结果

Figure 13. Cavity recoupling based on mode energy gradient ascent

下载: 全尺寸图片幻灯片

图 14 锁定激光到不同模式上

Figure 14. Laser frequency locking on different optical modes

下载: 全尺寸图片幻灯片

参考文献(25)

[1]	AASI J, ABBOTT B P, ABBOTT R, et al. Advanced LIGO[J]. Classical and Quantum Gravity, 2015, 32(7): 074001. doi: 10.1088/0264-9381/32/7/074001
[2]	AASI J, ABADIE J, ABBOTT B P, et al. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light[J]. Nature Photonics, 2013, 7(8): 613-619. doi: 10.1038/nphoton.2013.177
[3]	DANZMANN K, PRINCE T, BINETRUY P, et al. LISA: unveiling a hidden universe[R]. Paris: European Space Agency, 2011.
[4]	BLOOM B, NICHOLSON T L, WILLIAMS J R, et al. An optical lattice clock with accuracy and stability at the 10⁻¹⁸ level[J]. Nature, 2014, 506(7486): 71-75. doi: 10.1038/nature12941
[5]	DREVER R W P, HALL J L, KOWALSKI F V, et al. Laser phase and frequency stabilization using an optical resonator[J]. Applied Physics B, 1983, 31(2): 97-105.
[6]	CAHILLANE C, MANSELL G L, SIGG D. Laser frequency noise in next generation gravitational wave detectors[J]. Optics Express, 2021, 29: 42144-42161. doi: 10.1364/OE.439253
[7]	ROSI G, SORRENTINO F, CACCIAPUOTI L, et al. Precision measurement of the Newtonian gravitational constant using cold atoms[J]. Nature, 2014, 510(7506): 518-521. doi: 10.1038/nature13433
[8]	KESSLER T, HAGEMANN C, GREBING C, et al. A sub-40-mHz-linewidth laser based on a silicon single-crystal optical cavity[J]. Nature Photonics, 2012, 6(10): 687-692. doi: 10.1038/nphoton.2012.217
[9]	ANDERSON D Z. Alignment of resonant optical cavities[J]. Applied Optics, 1984, 23(17): 2944-2949. doi: 10.1364/AO.23.002944
[10]	MAVALVALA N. Alignment issues in laser interferometric gravitational-wave detectors[D]. Cambridge: Massachusetts Institute of Technology, 1997.
[11]	BOND C, BROWN D, FREISE A, et al. Interferometer techniques for gravitational-wave detection[J]. Living Reviews in Relativity, 2016, 19(1): 3. doi: 10.1007/s41114-016-0002-8
[12]	MORRISON E, MEERS B J, ROBERTSON D I, et al. Automatic alignment of optical interferometers[J]. Applied Optics, 1994, 33(22): 5041-5049. doi: 10.1364/AO.33.005041
[13]	MORRISON E, MEERS B J, ROBERTSON D I, et al. Experimental demonstration of an automatic alignment system for optical interferometers[J]. Applied Optics, 1994, 33(22): 5037-5040. doi: 10.1364/AO.33.005037
[14]	GROTE H, HEINZEL G, FREISE A, et al. The automatic alignment system of GEO 600[J]. Classical and Quantum Gravity, 2002, 19(7): 1849-1855. doi: 10.1088/0264-9381/19/7/384
[15]	SAYEH M R, BILGER H R, HABIB T. Optical resonator with an external source: excitation of the Hermite-Gaussian modes[J]. Applied Optics, 1985, 24(22): 3756-3761. doi: 10.1364/AO.24.003756
[16]	TAO L, KELLEY-DERZON J, GREEN A C, et al. Power coupling losses for misaligned and mode-mismatched higher-order Hermite–Gauss modes[J]. Optics Letters, 2021, 46(11): 2694-2697. doi: 10.1364/OL.426999
[17]	HOU Y. Control system for mirror tilting by deep learning[D]. Tokyo: Tokyo Institute of Technology, 2023.
[18]	MENG F CH, LI Z CH, LI J Q, et al. An active method for coupling laser with a high-finesse Fabry–Pérot cavity in ultra-stable lasers[J]. Optics & Laser Technology, 2024, 171: 110371.
[19]	DOSOVITSKIY A, BEYER L, KOLESNIKOV A, et al. An image is worth 16x16 words: transformers for image recognition at scale[C]. Proceedings of the 9th International Conference on Learning Representations, ICLR, 2021.
[20]	WANG C Y, BOCHKOVSKIY A, LIAO H Y M. YOLOv7: trainable bag-of-freebies sets new state-of-the-art for real-time object detectors[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, IEEE, 2023: 7464-7475.
[21]	KIRILLOV A, MINTUN E, RAVI N, et al. Segment anything[C]. Proceedings of the IEEE/CVF International Conference on Computer Vision, IEEE, 2023: 4015-4026.
[22]	SOROKIN D, ULANOV A, SAZHINA E, et al. Interferobot: aligning an optical interferometer by a reinforcement learning agent[C]. Proceedings of the 34th International Conference on Neural Information Processing Systems, Curran Associates Inc. , 2020: 1110.
[23]	SHAO R, ZHANG G, GONG X. Generalized robust training scheme using genetic algorithm for optical neural networks with imprecise components[J]. Photonics Research, 2022, 10(8): 1868-1876. doi: 10.1364/PRJ.449570
[24]	QIN J Y, KINDER K, JADHAV S, et al. Automated alignment of an optical cavity using machine learning[J]. Classical and Quantum Gravity, 2025, 42(4): 045003. doi: 10.1088/1361-6382/ada864
[25]	TAN M X, LE Q V. EfficientNet: rethinking model scaling for convolutional neural networks[C]. Proceedings of the 36th International Conference on Machine Learning, ICML, 2019: 6105-6114.