Iterative estimation and precision suppression of inter- spacecraft tilt-to-length coupling noise for the Taiji space gravitational wave detection mission
-
摘要:
太极空间引力波探测任务采用激光干涉方法测量由引力波引起的皮米尺度距离变化。卫星和可移动光学组件（MOSA）姿态抖动引起的星间姿态-光程耦合噪声（TTL），将显著降低对引力波信号的灵敏度。为此需要在数据处理阶段拟合和扣除TTL噪声。本文针对卫星和MOSA的姿态抖动，提出了一种星间TTL噪声抑制算法。首先，对TTL噪声进行一阶线性近似建模，并引入时间延迟干涉（TDI）组合中，得到它在TDI输出中的表现形式；接着，通过比较TDI数据与TDI组合后的TTL噪声模型，建立似然函数；然后，通过极大似然法初步估计TTL耦合系数，从TDI数据中扣除初步拟合的TTL噪声，可估计出残余底噪的统计性质并重新代入似然函数，再次执行TTL耦合系数的极大似然估计；将上述步骤迭代十次，可获得精确的底噪模型；最后，通过马尔可夫链蒙特卡洛（MCMC）方法得到TTL系数的后验分布，完成TTL噪声的精确拟合，从而实现噪声的有效抑制。结果表明，80%以上的系数估计值都在三个标准差内，80%以上的系数估计与真值相差小于0.1 mm/rad。对于不同水平的TTL系数，抑制后的残余TTL噪声都比次级噪声低一个量级，具有一定鲁棒性，尤其适用于底噪模型未知的实际探测场景，满足空间引力波探测需求。
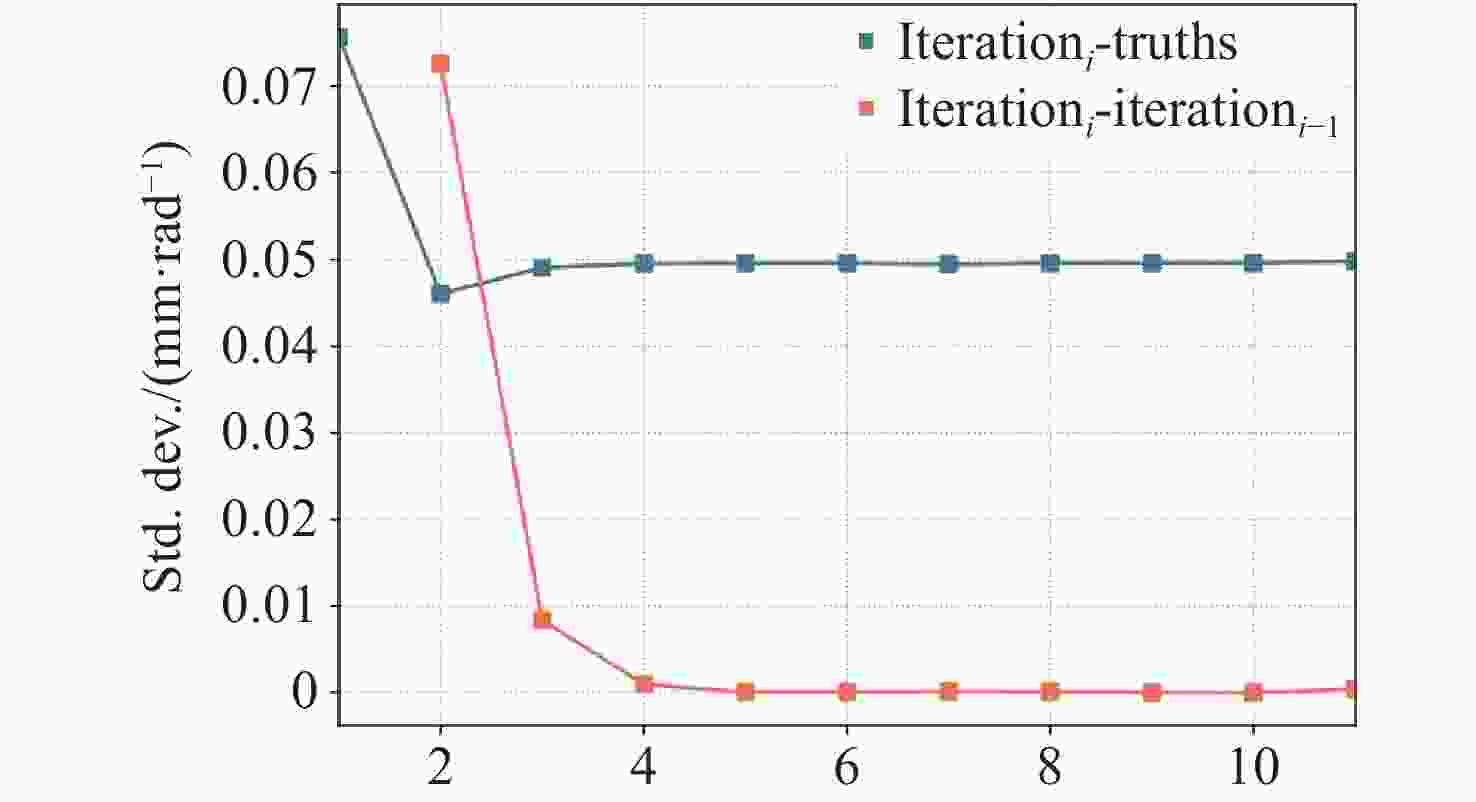
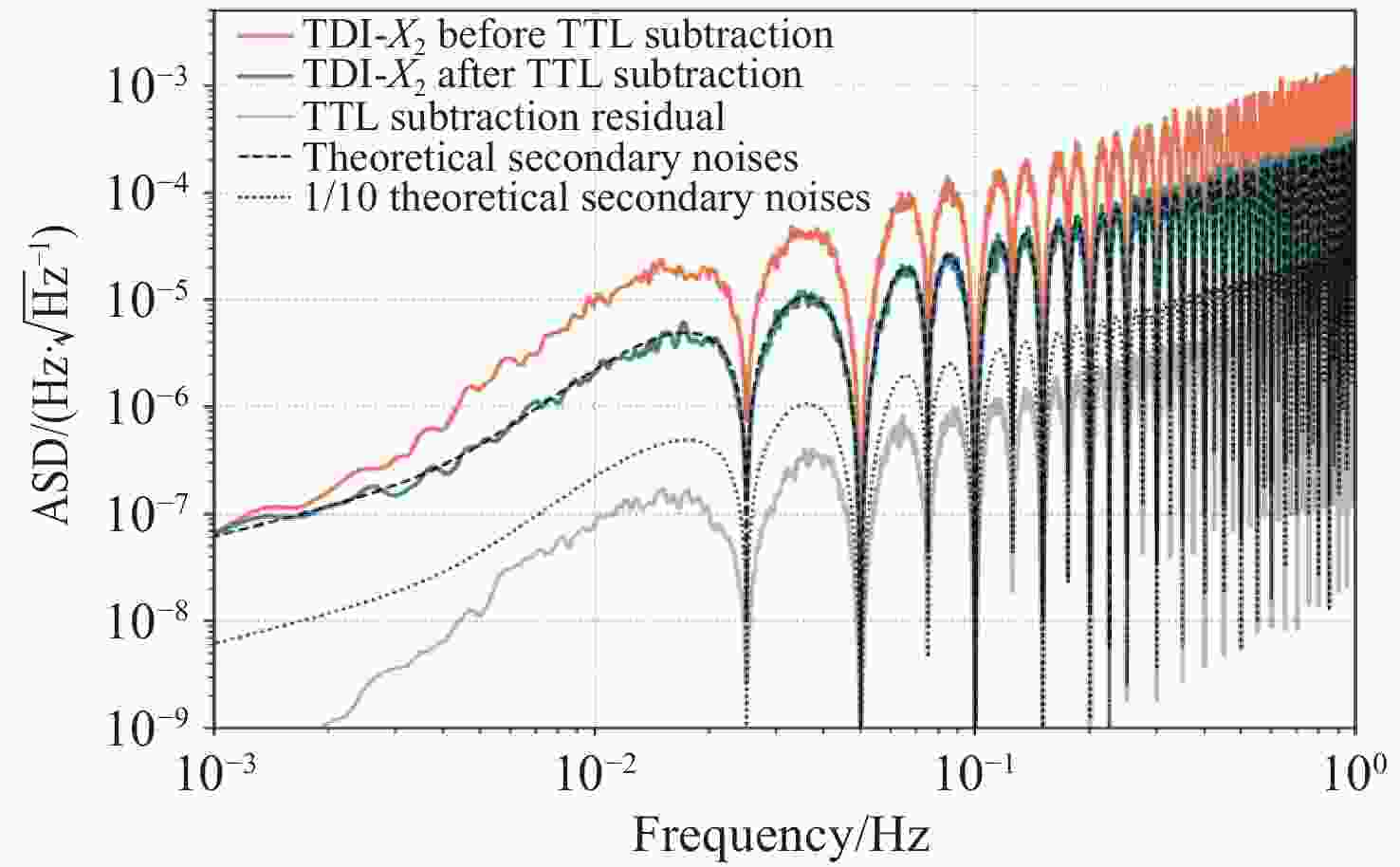
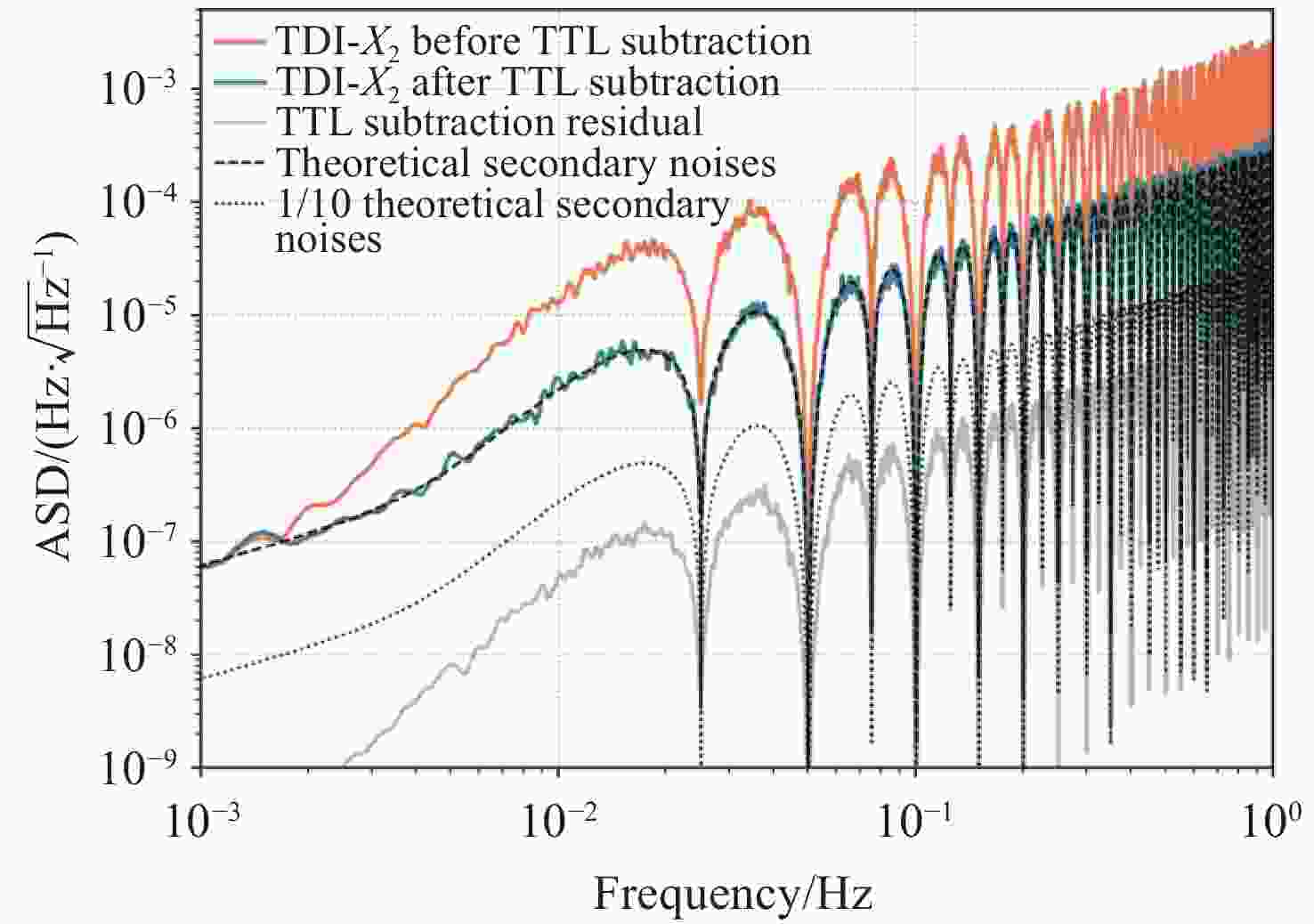
Abstract:The Taiji space gravitational wave detection mission employs laser interferometry to measure picometer-level distance variations induced by gravitational waves. Attitude jitter in both satellites and movable optical subassemblies (MOSA) generates tilt-to-length (TTL) coupling noise that critically degrades detection sensitivity. Therefore, it is necessary to fit and subtract TTL noise during the data processing stage. To address this challenge, we propose an iterative TTL noise suppression algorithm for post-processing. First, a first-order linear approximation model of TTL noise is established and incorporated into the time-delay interferometry (TDI) combinations to derive its expression in TDI outputs. We subsequently perform initial maximum likelihood estimation of the TTL coupling coefficients, subtract the preliminary TTL noise estimate from the TDI data to characterize the residual baseline noise statistics, and reincorporate these statistics into the updated likelihood function for subsequent TTL coefficient estimation. Through ten iterative cycles, we achieve a refined baseline noise model. Finally, The posterior distribution of the TTL coefficients is obtained via the Markov Chain Monte Carlo (MCMC) method, thereby accomplishing the precise fitting of the TTL noise and consequently achieving effective noise suppression. Results demonstrate that over 80% of estimated coefficients fall within three standard deviations, and more than 80% of the coefficient estimates deviate from the true values by less than 0.1 mm/rad. For various levels of TTL coefficients, the residual TTL noise after suppression is one order of magnitude lower than the secondary noise, demonstrating a certain degree of robustness. This is particularly applicable to real detection scenarios where the noise floor model is unknown, meeting the requirements for space-based gravitational wave detection.
-
图 1 太极计划三星编队示意图与标号规定。
Figure 1. Schematic diagram and labeling conventions of Taiji's 3-spacecraft.
图 3 MOSA12、MOSA13和SC1的坐标系。
Figure 3. The coordinate system of SC1 and the two MOSAs mounted on it.
图 4 测量数据数值仿真过程与TTL系数迭代拟合与消除抑制算法流程图
Figure 4. The flowchart of data simulation and TTL coefficient estimation.
图 8 基准TTL噪声系数为2.3 mm/rad时X2通道的噪声抑制结果
Figure 8. The subtraction results of the X2 channel with fiducial TTL coefficients at the 2.3 mm/rad level.
图 9 基准TTL噪声系数为10mm/rad时X2通道的噪声抑制结果
Figure 9. The subtraction results of the X2 channel with fiducial TTL coefficients at the 10 mm/rad level.
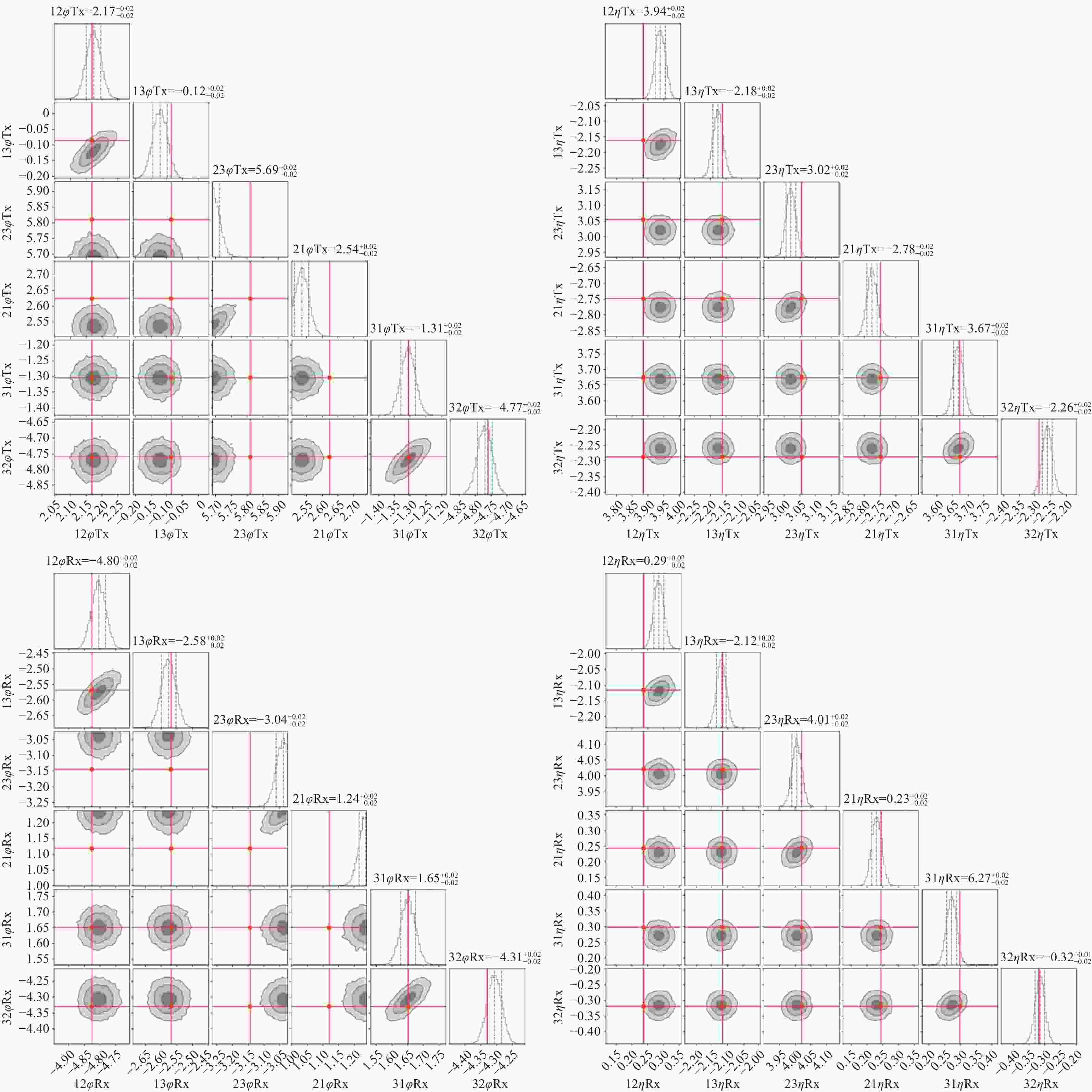
表 1 系数真值与估计结果（单位：mm/rad）
Table 1. Coefficient true value and estimated result (unit: mm/rad)
系数 真值 第一次
MLE结果第一次
MLE误差最终MCMC
估计结果最终MCMC
估计误差$ {{{C}}_{12\varphi Tx}} $ 2.168 2.275 0.107 2.173 0.005 $ {{{C}}_{13\varphi Tx}} $ −0.086 0.082 0.168 −0.121 −0.035 $ {{{C}}_{23\varphi Tx}} $ 5.811 5.847 0.037 5.689 −0.121 $ {{{C}}_{21\varphi Tx}} $ 2.624 2.640 0.017 2.535 −0.089 $ {{{C}}_{31\varphi Tx}} $ −1.304 −1.313 −0.009 −1.306 −0.001 $ {{{C}}_{32\varphi Tx}} $ −4.760 −4.801 −0.041 −4.770 −0.010 $ {{{C}}_{12\eta Tx}} $ 3.885 3.973 0.088 3.939 0.054 $ {{{C}}_{13\eta Tx}} $ −2.161 −2.220 −0.058 −2.175 −0.014 $ {{{C}}_{23\eta Tx}} $ 3.055 3.014 −0.041 3.021 −0.034 $ {{{C}}_{21\eta Tx}} $ −2.748 −2.890 −0.142 −2.776 −0.028 $ {{{C}}_{31\eta Tx}} $ 3.673 3.697 0.023 3.669 −0.004 $ {{{C}}_{32\eta Tx}} $ −2.287 −2.202 0.085 −2.260 0.027 $ {{{C}}_{12\varphi Rx}} $ −4.826 −4.852 −0.025 −4.805 0.022 $ {{{C}}_{13\varphi Rx}} $ −2.568 −2.737 −0.168 −2.576 −0.007 $ {{{C}}_{23\varphi Rx}} $ −3.145 −3.072 0.073 −3.039 0.106 $ {{{C}}_{21\varphi Rx}} $ 1.119 1.129 0.010 1.237 0.118 $ {{{C}}_{31\varphi Rx}} $ 1.652 1.693 0.041 1.651 −0.001 $ {{{C}}_{32\varphi Rx}} $ −4.330 −4.304 0.025 −4.306 0.023 $ {{{C}}_{12\eta {\mathrm{Rx}}}} $ 0.236 0.354 0.118 0.285 0.049 $ {{{C}}_{13\eta {\mathrm{Rx}}}} $ −2.116 −2.118 −0.002 −2.120 −0.004 $ {{{C}}_{23\eta {\mathrm{Rx}}}} $ 4.021 3.984 −0.037 4.005 −0.016 $ {{{C}}_{21\eta {\mathrm{Rx}}}} $ 0.244 0.313 0.069 0.230 −0.013 $ {{{C}}_{31\eta {\mathrm{Rx}}}} $ 6.298 6.279 −0.019 6.271 −0.027 $ {{{C}}_{32\eta {\mathrm{Rx}}}} $ −0.318 −0.336 −0.018 −0.315 0.003 
下载: 导出CSV
-
[1] SATHYAPRAKASH B S, SCHUTZ B F. Physics, astrophysics and cosmology with gravitational waves[J]. Living Reviews in Relativity, 2009, 12(1): 2. doi: 10.12942/lrr-2009-2 [2] GONG X F, XU SH N, YUAN Y F, et al. Laser interferometric gravitational wave detection in space and structure formation in the early universe[J]. Chinese Astronomy and Astrophysics, 2015, 39(4): 411-446. doi: 10.1016/j.chinastron.2015.10.001 [3] AASI J, ABBOTT B P, ABBOTT R, et al. Advanced LIGO[J]. Classical and Quantum Gravity, 2015, 32(7): 074001. doi: 10.1088/0264-9381/32/7/074001 [4] BABAK S, GAIR J, SESANA A, et al. Science with the space-based interferometer LISA. V. Extreme mass-ratio inspirals[J]. Physical Review D, 2017, 95(10): 103012. doi: 10.1103/PhysRevD.95.103012 [5] BERTI E, CARDOSO V, WILL C M. Gravitational-wave spectroscopy of massive black holes with the space interferometer LISA[J]. Physical Review D, 2006, 73(6): 064030. doi: 10.1103/PhysRevD.73.064030 [6] SCHUTZ B F. Introduction to the analysis of low-frequency gravitational wave data[J]. arXiv: gr-qc/9710080, 1997. (查阅网上资料, 不确定文献类型及格式是否正确, 请确认) . [7] CYRANOSKI D. Chinese gravitational-wave hunt hits crunch time[J]. Nature, 2016, 531(7593): 150-151. doi: 10.1038/531150a [8] HU W R, WU Y L. The Taiji Program in Space for gravitational wave physics and the nature of gravity[J]. National Science Review, 2017, 4(5): 685-686. doi: 10.1093/nsr/nwx116 [9] 罗子人, 张敏, 靳刚, 等. 中国空间引力波探测“太极计划”及“太极1号”在轨测试[J]. 深空探测学报,2020,7(1):3-10.LUO Z R, ZHANG M, JIN G, et al. Introduction of Chinese space-borne gravitational wave detection program “Taiji” and “Taiji-1” satellite mission[J]. Journal of Deep Space Exploration, 2020, 7(1): 3-10. (in Chinese). [10] CAI R G, CAO ZH J, GUO Z K, et al. The gravitational-wave physics[J]. National Science Review, 2017, 4(5): 687-706. doi: 10.1093/nsr/nwx029 [11] LUO Z R, GUO Z K, JIN G, et al. A brief analysis to Taiji: science and technology[J]. Results in Physics, 2020, 16: 102918. doi: 10.1016/j.rinp.2019.102918 [12] LUO Z R, WANG Y, WU Y L, et al. The Taiji program: a concise overview[J]. Progress of Theoretical and Experimental Physics, 2021, 2021(5): 05A108. doi: 10.1093/ptep/ptaa083 [13] LUO Z R, ZHANG M, WU Y L. Recent status of Taiji program in China[J]. Chinese Journal of Space Science, 2022, 42(4): 536-538. doi: 10.11728/cjss2022.04.yg03 [14] ZHAO M Y, PENG X D, YANG ZH, et al. Preliminary simulation of intersatellite laser interference link for the Taiji program[J]. Journal of Astronomical Telescopes, Instruments, and Systems, 2022, 8(3): 038002. [15] TINTO M, ARMSTRONG J W. Cancellation of laser noise in an unequal-arm interferometer detector of gravitational radiation[J]. Physical Review D, 1999, 59(10): 102003. doi: 10.1103/PhysRevD.59.102003 [16] ARMSTRONG J W, ESTABROOK F B, TINTO M. Time - delay interferometry for space - based gravitational wave searches[J]. The Astrophysical Journal, 1999, 527(2): 814-826. doi: 10.1086/308110 [17] STAAB M, LILLEY M, BAYLE J B, et al. Laser noise residuals in LISA from on - board processing and time - delay interferometry[J]. Physical Review D, 2024, 109(4): 043040. doi: 10.1103/PhysRevD.109.043040 [18] BAYLE J B, HARTWIG O, STAAB M. Adapting time - delay interferometry for LISA data in frequency[J]. Physical Review D, 2021, 104(2): 023006. doi: 10.1103/PhysRevD.104.023006 [19] VALLISNERI M, BAYLE J B, BABAK S, et al. Time - delay interferometry without delays[J]. Physical Review D, 2021, 103(8): 082001. doi: 10.1103/PhysRevD.103.082001 [20] NAM D Q, LEMIERE Y, PETITEAU A, et al. TDI noises transfer functions for LISA[J]. arXiv preprint arXiv: 2211.02539, 2022. (查阅网上资料, 不确定文献类型及格式是否正确, 请确认) . [21] TINTO M, DHURANDHAR S V. Time-delay interferometry[J]. Living Reviews in Relativity, 2021, 24(1): 1. doi: 10.1007/s41114-020-00029-6 [22] ARMANO M, AUDLEY H, BAIRD J, et al. LISA Pathfinder platform stability and drag-free performance[J]. Physical Review D, 2019, 99(8): 082001. doi: 10.1103/PhysRevD.99.082001 [23] ARMA NO M, AUDLEY H, BAIRD J, et al. Lisa pathfinder[C]. Proceedings of the 28th International Symposium on Lepton Photon Interactions at High Energies, Sun Yat-sen University, 2020: 185-204. [24] HARTIG M S, SCHUSTER S, WANNER G. Geometric tilt-to-length coupling in precision interferometry: mechanisms and analytical descriptions[J]. Journal of Optics, 2022, 24(6): 065601. doi: 10.1088/2040-8986/ac675e [25] TAO Y ZH, GAO R H, JIN H B, et al. Approximate model for the coupling of far-field wavefront errors and jitter in space- based gravitational wave laser interferometry[J]. arXiv preprint arXiv: 2410.22914, 2024. (查阅网上资料, 不确定文献类型及格式是否正确, 请确认) . [26] LUO Z R, WANG Q L, MAHRDT C, et al. Possible alternative acquisition scheme for the gravity recovery and climate experiment follow-on-type mission[J]. Applied Optics, 2017, 56(5): 1495-1500. doi: 10.1364/AO.56.001495 [27] WUCHENICH D M R, MAHRDT C, SHEARD B S, et al. Laser link acquisition demonstration for the GRACE Follow-On mission[J]. Optics Express, 2014, 22(9): 11351-11366. doi: 10.1364/OE.22.011351 [28] PACZKOWSKI S, GIUSTERI R, HEWITSON M, et al. Postprocessing subtraction of tilt-to-length noise in LISA[J]. Physical Review D, 2022, 106(4): 042005. doi: 10.1103/PhysRevD.106.042005 [29] ARMANO M, AUDLEY H, BAIRD J, et al. Tilt-to-length coupling in LISA Pathfinder: a data analysis[J]. Physical Review D, 2023, 108(10): 102003. doi: 10.1103/PhysRevD.108.102003 [30] GEORGE D, SANJUAN J, FULDA P, et al. Calculating the precision of tilt-to-length coupling estimation and noise subtraction in LISA using Fisher information[J]. Physical Review D, 2023, 107(2): 022005. doi: 10.1103/PhysRevD.107.022005 [31] HOUBA N, DELCHAMBRE S, HECHENBLAIKNER G, et al. Time-delay interferometry infinity for tilt-to-length noise estimation in LISA[J]. Classical and Quantum Gravity, 2023, 40(10): 107001. doi: 10.1088/1361-6382/accbfc [32] HARTIG M S, PACZKOWSKI S, HEWITSON M, et al. Post-processing subtraction of tilt-to-length noise in LISA in the presence of gravitational wave signals[J]. arXiv preprint arXiv: 2411.14191, 2024. (查阅网上资料, 不确定文献类型及格式是否正确, 请确认) . [33] 王娟, 齐克奇, 王少鑫, 等. 面向空间引力波探测的激光干涉技术研究进展及展望[J]. 中国科学: 物理学 力学 天文学,2024,54(7):270405.WANG J, QI K Q, WANG SH X, et al. Advance and prospect in the study of laser interferometry technology for space gravitational wave detection[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2024, 54(7): 270405. (in Chinese). [34] SHEN J, WANG SH X, QI K Q, et al. The suppression effect of an imaging system on the geometric tilt-to-length coupling in a test mass interferometer[J]. Photonics, 2024, 11(7): 638. doi: 10.3390/photonics11070638 [35] WANNER G, SHAH S, STAAB M, et al. In-depth modeling of tilt-to-length coupling in LISA’s interferometers and TDI Michelson observables[J]. Physical Review D, 2024, 110(2): 022003. doi: 10.1103/PhysRevD.110.022003 [36] WANNER G, HEINZEL G, KOCHKINA E, et al. Methods for simulating the readout of lengths and angles in laser interferometers with Gaussian beams[J]. Optics Communications, 2012, 285(24): 4831-4839. doi: 10.1016/j.optcom.2012.07.123 [37] 王智, 沙巍, 陈哲, 等. 空间引力波探测望远镜初步设计与分析[J]. 中国光学,2018,11(1):131-151. doi: 10.3788/co.20181101.0131WANG ZH, SHA W, CHEN ZH, et al. Preliminary design and analysis of telescope for space gravitational wave detection[J]. Chinese Optics, 2018, 11(1): 131-151. (in Chinese). doi: 10.3788/co.20181101.0131 [38] 徐乾蛟, 崔冰, 王鹏程, 等. 空间引力波探测无拖曳卫星有限频域抗扰控制器设计[J]. 空间科学学报,2024,44(5):903-916. doi: 10.11728/cjss2024.05.2024-0022XU Q J, CUI B, WANG P CH, et al. Design of finite frequency domain disturbance rejection controller for the drag-free spacecraft in space-borne gravitational wave detection[J]. Chinese Journal of Space Science, 2024, 44(5): 903-916. doi: 10.11728/cjss2024.05.2024-0022 [39] STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. doi: 10.1023/A:1008202821328 [40] KARNESIS N, KATZ M L, KORSAKOVA N, et al. Eryn: a multi-purpose sampler for Bayesian inference[J]. arXiv preprint arXiv: 2303.02164, 2023. (查阅网上资料, 不确定文献类型及格式是否正确, 请确认) . [41] KATZ M, KARNESIS N, KORSAKOVA N. mikekatz04 Eryn: first full release[S]. Zenodo, 2023. (查阅网上资料, 未找到本条文献出版地信息, 请确认) . -
下载:
计量
- 文章访问数: 33
- HTML全文浏览量: 10
- PDF下载量: 6
- 被引次数: 0
