Ultralow residual phase noise frequency synthesizer for space gravitational wave detection
-
摘要:
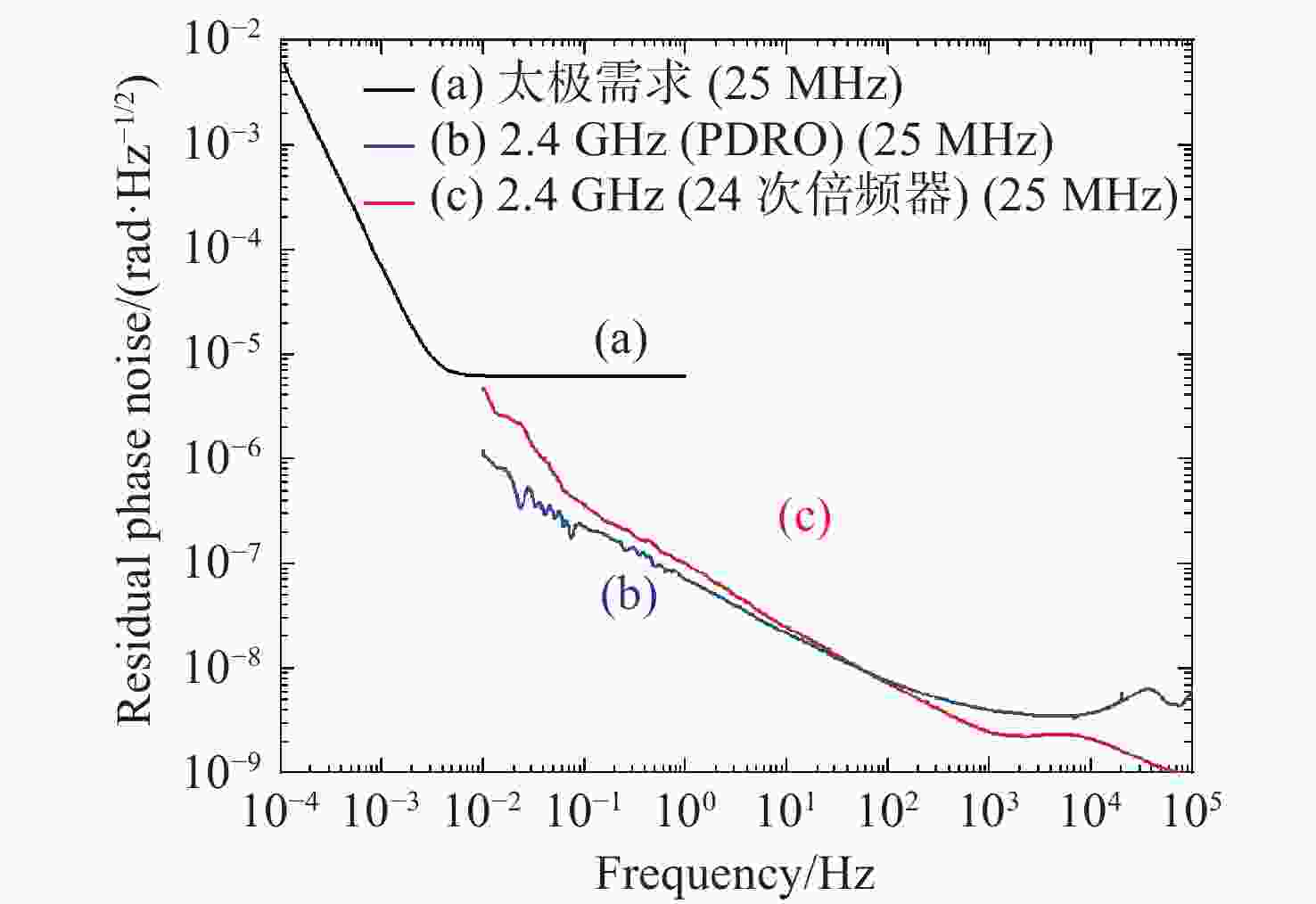
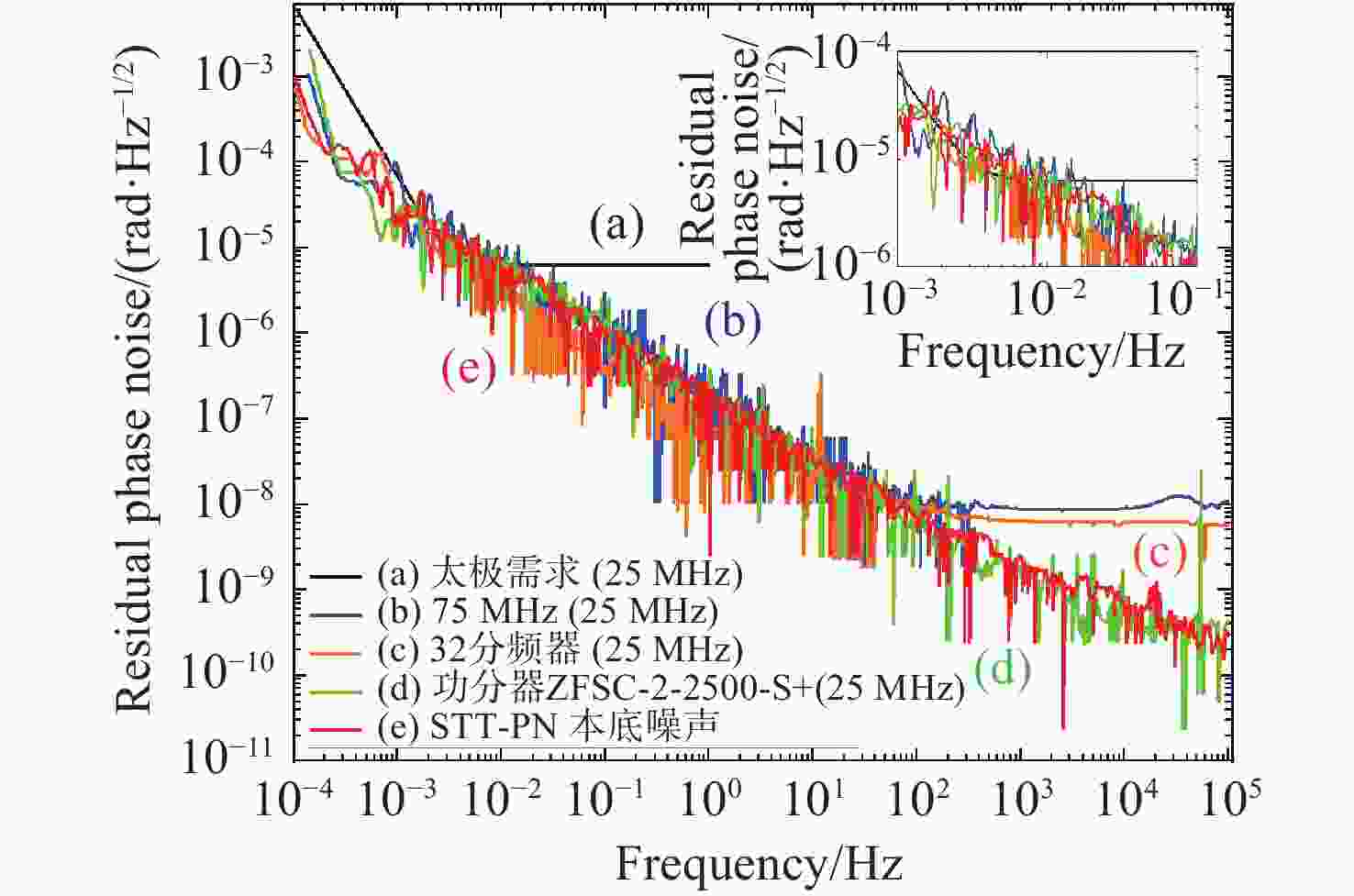
基于激光干涉的空间引力波探测对毫赫兹频段内的时钟噪声抑制水平提出了极高要求,通常通过边带倍频时钟噪声传递和导频音等技术来抑制时钟噪声。针对时钟噪声抑制技术需要的超低附加相噪的电光调制器(EOM)调制微波(2.4 GHz)和导频音射频信号(75 MHz),本文设计、搭建并比较了两种微波合成链路。通过低相噪锁相介质振荡器(PDRO)、分频等技术,实现了超低附加相噪频综。经测量,75 MHz导频信号在0.1 mHz、1 mHz、10 mHz、100 mHz、1 Hz处相对应的残余相噪分别为
$ 1.06\times {10}^{-3}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ ,$ 8.18\times {10}^{-5}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ ,$ 7.63\times {10}^{-6}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ ,$ 1.30\times {10}^{-6}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ ,$ 1.53\times {10}^{-7}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ 。该导频信号是经2.4 GHz微波分频产生的,后者的残余相噪更低,因而在20 mHz~1 Hz 频段内,两者的残余相噪都满足“太极计划”需要。后期经过降低功分、频分等器件的附加相位噪声、减小关键器件的温度敏感度及增加温度控制、导频校正等技术,还可进一步降低该频综的本底噪声,有望在0.1 mHz-1 Hz的整个频段内都满足“太极计划”需求。本文对于频综的研究结果为我国空间引力波探测需要的时频系统研制奠定了坚实基础。Abstract:A space laser interferometric gravitational wave observatory requires spaceborne clocks with ultralow phase noise in the millihertz frequency band. Such noise can be suppressed using a sideband multiplication transfer scheme and pilot tone techniques. To meet the requirements of the clock noise suppression technique, ultralow residual phase noise synthesizers are required to generate the microwave (2.4 GHz) for electro-optic modulator modulation and the pilot tone signal (75 MHz). To this end, two different structures of microwave chains have been designed, implemented and compared. The application of low phase noise phase-locked dielectric resonator oscillators (PDROs) and frequency division techniques enabled the development of a frequency synthesis chain with ultralow residual phase noise. The residual phase noise of the 75 MHz pilot signal is measured to be
$ 1.06\times {10}^{-3}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ ,$ 8.18\times {10}^{-5}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ ,$ 7.63\times {10}^{-6}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ ,$ 1.30\times {10}^{-6}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ and$ 1.53\times {10}^{-7}\;\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ at Fourier frequencies of 0.1 mHz, 1 mHz, 10 mHz, 100 mHz, and 1 Hz, respectively. The pilot signal is generated by frequency division of a 2.4 GHz microwave signal, thus it's residual phase noise is lower. As a result, the residual phase noise levels of both signals meet the requirements of the "Taiji Program" in the range of 20 mHz to 1 Hz. By further reducing the residual phase noise of power dividers, frequency dividers and other devices, reducing the temperature sensitivity of key devices, and adding temperature control and pilot tone correction technologies, the noise floor of the frequency synthesizer can be further reduced to meet the requirements of the Taiji Project in the entire frequency range (0.1 mHz−1 Hz). The development of this frequency synthesizer lays a solid foundation for the time-frequency system required for China's space gravitational wave detection. -
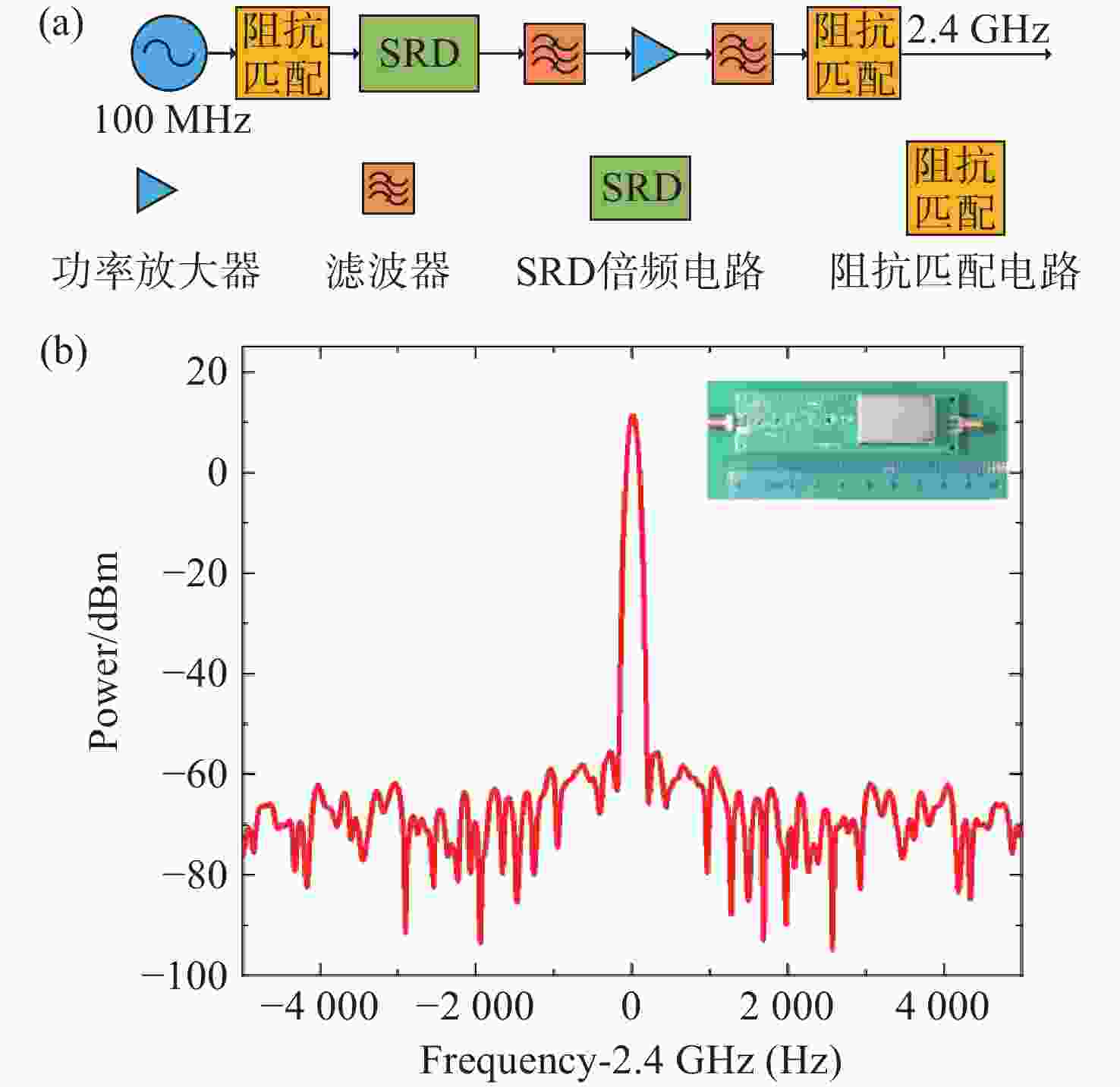
图 2 (a)24次直接倍频器原理框图。(b)24次倍频器频谱图。插图:24次倍频器模块实物图。频谱仪的分辨率带宽(Resolution Bandwidth,RBW)和视频带宽(Video Bandwidth,VBW)均为91 Hz
Figure 2. (a) Principle diagram and (b) spectrum diagram of a 24th-order direct frequency multiplier. Illustration: physical photo of the 24th-order frequency multiplier. The RBW and VBW of the spectrum analyzer are both 91 Hz
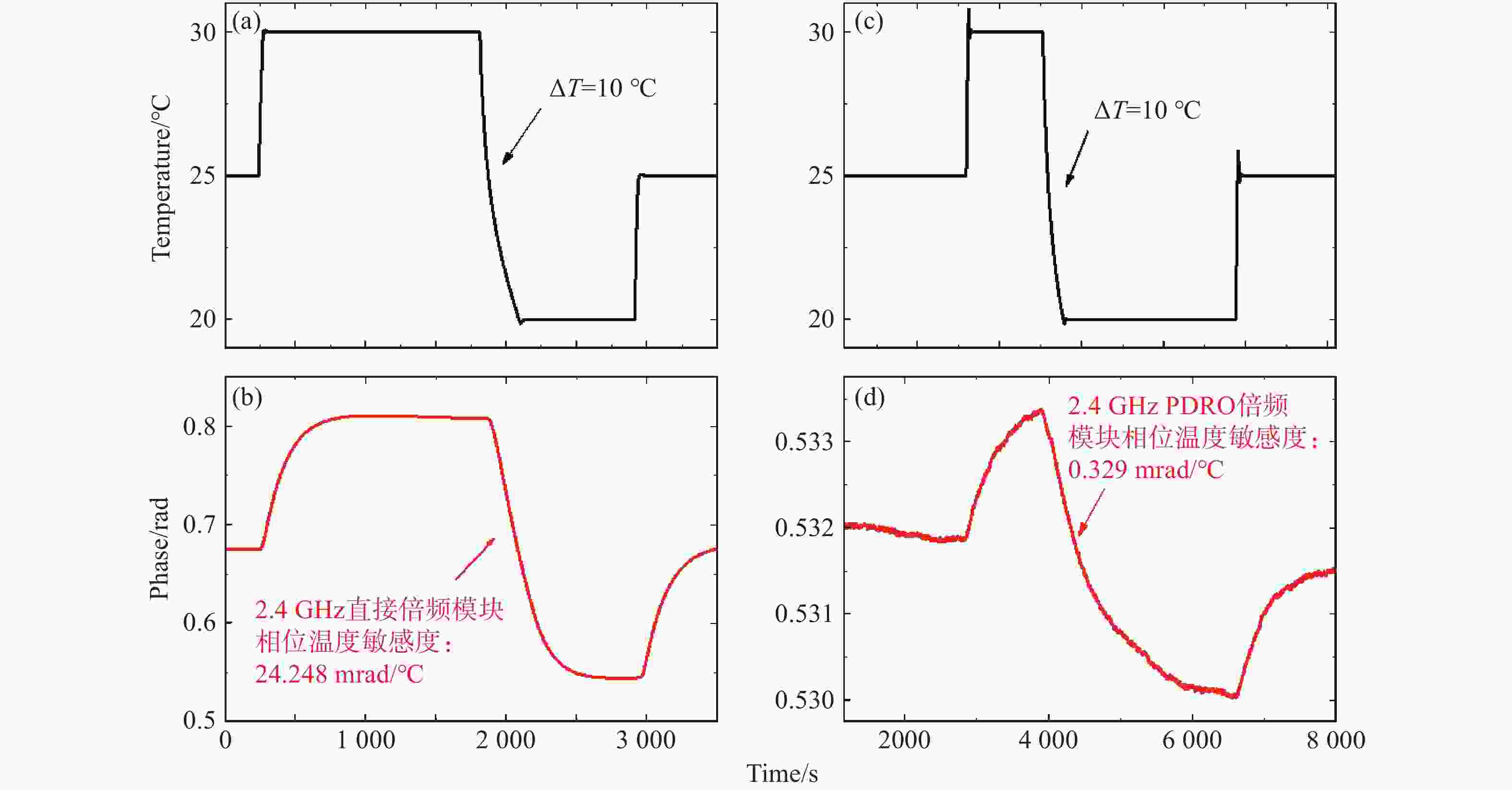
图 8 相位温度敏感度实验结果。(a)、(c)温度变化顺序。(b)24次倍频链路输出微波相位的温度敏感度。(d)PDRO链路输出微波相位的温度敏感度
Figure 8. Experimental results of phase temperature sensitivity. (a) and (c) represent temperature variation sequence; (b) temperature sensitivity of the output microwave phase in the 24-order frequency multiplication system; (d) temperature sensitivity of the output microwave phase in the PDRO
表 1 残余相噪测量结果与太极计划需求
Table 1. Residual phase noise measurement results and Taiji program requirements
(rad·Hz ${}^{-\frac{1}{2}} $ )频偏 太极计划残余相噪
需求2.4 GHz频综
残余相噪75 MHz频综
残余相噪0.1 mHz $ 5.79\times {10}^{-3} $ $ \leqslant 1.06\times {10}^{-3} $ $ 1.06\times {10}^{-3} $ 1 mHz $ 5.93\times {10}^{-5} $ $ \leqslant 8.18\times {10}^{-5} $ $ 8.18\times {10}^{-5} $ 10 mHz $ 6.30\times {10}^{-6} $ $ 1.19\times {10}^{-6} $ $ 7.63\times {10}^{-6} $ 100 mHz $ 6.28\times {10}^{-6} $ $ 2.22\times {10}^{-7} $ $ 1.30\times {10}^{-6} $ 1 Hz $ 6.28\times {10}^{-6} $ $ 6.96\times {10}^{-8} $ $ 1.53\times {10}^{-7} $ -
[1] 吴岳良,胡文瑞, 王建宇, 等. 空间引力波探测综述与拟解决的科学问题[J]. 空间科学学报,2023,43(4):589-599.WU Y L, HU W R, WANG J Y, et al. Review and scientific objectives of spaceborne gravitational wave detection missions (in Chinese)[J]. Chinese Journal of Space Science, 2023, 43(4): 589-599. [2] BARKE S, BRAUSE N, BYKOV I, et al. LISA metrology system - final report[R]. Lyngby: Denmark Technical University of Denmark, 2014. [3] ARMANO M, AUDLEY H, AUGER G, et al. Sub-femto-g free fall for space-based gravitational wave observatories: LISA pathfinder results[J]. Physical Review Letters, 2016, 116(23): 231101. doi: 10.1103/PhysRevLett.116.231101 [4] ARMANO M, AUDLEY H, BAIRD J, et al. Sensor noise in LISA Pathfinder: in-flight performance of the optical test mass readout[J]. Physical Review Letters, 2021, 126(13): 131103. doi: 10.1103/PhysRevLett.126.131103 [5] ARMANO M, AUDLEY H, BAIRD J, et al. Beyond the required LISA free-fall performance: new LISA pathfinder results down to 20 μHz[J]. Physical Review Letters, 2018, 120(6): 061101. doi: 10.1103/PhysRevLett.120.061101 [6] ARMANO M, AUDLEY H, BAIRD J, et al. LISA pathfinder performance confirmed in an open-loop configuration: results from the free-fall actuation mode[J]. Physical Review Letters, 2019, 123(11): 111101. doi: 10.1103/PhysRevLett.123.111101 [7] WANNER G. Space-based gravitational wave detection and how LISA pathfinder successfully paved the way[J]. Nature Physics, 2019, 15(3): 200-202. doi: 10.1038/s41567-019-0462-3 [8] HU W R, WU Y L. The Taiji program in space for gravitational wave physics and the nature of gravity[J]. National Science Review, 2017, 4(5): 685-686. doi: 10.1093/nsr/nwx116 [9] WU Y L, LUO Z R, WANG J Y, et al. China’s first step towards probing the expanding universe and the nature of gravity using a space borne gravitational wave antenna[J]. Communications Physics, 2021, 4(1): 34. doi: 10.1038/s42005-021-00529-z [10] LUO J, BAI Y ZH, CAI L, et al. The first round result from the TianQin-1 satellite[J]. Classical and Quantum Gravity, 2020, 37(18): 185013. doi: 10.1088/1361-6382/aba66a [11] LUO J, CHEN L SH, DUAN H Z, et al. TianQin: a space-borne gravitational wave detector[J]. Classical and Quantum Gravity, 2016, 33(3): 035010. doi: 10.1088/0264-9381/33/3/035010 [12] HUANG SH J, HU Y M, KOROL V, et al. Science with the TianQin observatory: preliminary results on galactic double white dwarf binaries[J]. Physical Review D, 2020, 102(6): 063021. doi: 10.1103/PhysRevD.102.063021 [13] 罗俊, 艾凌皓, 艾艳丽, 等. 天琴计划简介[J]. 中山大学学报(自然科学版),2021,60(1-2):1-19.LUO J, AI L H, AI Y L, et al. A brief introduction to the TianQin project[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2021, 60(1-2): 1-19. (in Chinese). [14] KLIPSTEIN W, HALVERSON P G, PETERS R, et al. Clock noise removal in LISA[J]. AIP Conference Proceedings, 2006, 873(1): 312-318. [15] BARKE S. Inter-spacecraft frequency distribution for future gravitational wave observatories[D]. Hannover: Leibniz University, 2015. [16] BARKE S, TRÖBS M, SHEARD B, et al. EOM sideband phase characteristics for the spaceborne gravitational wave detector LISA[J]. Applied Physics B, 2010, 98(1): 33-39. doi: 10.1007/s00340-009-3682-x [17] ESTEBAN J J, GARCÍA A F, BARKE S, et al. Experimental demonstration of weak-light laser ranging and data communication for LISA[J]. Optics Express, 2011, 19(17): 15937-15946. doi: 10.1364/OE.19.015937 [18] WAND V, GUZMÁN F, HEINZEL G, et al. LISA phasemeter development[J]. AIP Conference Proceedings, 2006, 873(1): 689-696. [19] GERBERDING O. Phase readout for satellite interferometry[D]. Hannover: Gottfried Wilhelm Leibniz Universität Hannover, 2014. [20] GERBERDING O, DIEKMANN C, KULLMANN J, et al. Readout for intersatellite laser interferometry: measuring low frequency phase fluctuations of high-frequency signals with microradian precision[J]. Review of Scientific Instruments, 2015, 86(7): 074501. doi: 10.1063/1.4927071 [21] LIANG Y R. Note: a new method for directly reducing the sampling jitter noise of the digital phasemeter[J]. Review of Scientific Instruments, 2018, 89(3): 036106. doi: 10.1063/1.5011654 [22] DE VINE G, WARE B, MCKENZIE K, et al. Experimental demonstration of time-delay interferometry for the laser interferometer space antenna[J]. Physical Review Letters, 2010, 104(21): 211103. doi: 10.1103/PhysRevLett.104.211103 [23] 江强, 董鹏, 刘河山, 等. 太极计划时钟噪声传递的地面原理验证[J]. 中国光学(中英文),2023,16(6):1394-1403. doi: 10.37188/CO.2023-0012JIANG Q, DONG P, LIU H SH, et al. Ground-based principle verification of clock noise transfer for the Taiji program[J]. Chinese Optics, 2023, 16(6): 1394-1403. doi: 10.37188/CO.2023-0012 [24] ZENG H Y, YAN H, XIE S Y, et al. Experimental demonstration of weak-light inter-spacecraft clock jitter readout for TianQin[J]. Optics Express, 2023, 31(21): 34648-34666. doi: 10.1364/OE.503164 [25] TANG A, SUMNER T J. Removing the trend of drift induced from acceleration noise for LISA[J]. arXiv: 1202.2976, 2012. [26] COLPI M, DANZMANN K, HEWITSON M, et al. LISA definition study report[J]. arXiv: 2402.07571, 2024. [27] JU B W, YUN P, HAO Q, et al. A low phase and amplitude noise microwave source for vapor cell atomic clocks[J]. Review of Scientific Instruments, 2022, 93(10): 104709. doi: 10.1063/5.0096589 [28] LI W B, HAO Q, DU Y B, et al. Demonstration of a sub-sampling phase lock loop based microwave source for reducing dick effect in atomic clocks[J]. Chinese Physics Letters, 2019, 36(7): 070601. doi: 10.1088/0256-307X/36/7/070601 [29] LI X D, YUN P, LI Q L, et al. A low phase noise microwave source for high‐performance CPT Rb atomic clock[J]. Electronics Letters, 2021, 57(17): 659-661. doi: 10.1049/ell2.12222 [30] 温智强, 云恩学, 孙思宇, 等. 微波功率锁定的高性能CPT原子钟频综[J]. 计量学报,2025,46(2):267-273.WEN ZH Q, YUN E X, SUN S Y, et al. A power stabilized low noise frequency synthesizer for CPT atomic clocks[J]. Acta Metrologica Sinica, 2025, 46(2): 267-273. (in Chinese). [31] 薛正辉, 杨仕明, 李伟明, 等. 微波固态电路[M]. 北京: 北京理工大学出版社, 2004.XUE ZH H, YANG SH M, LI W M, et al. Microwave Solid State Circuit[M]. Beijing: Beijing Institute of Technology Press, 2004. [32] 赖寒昱, 李光灿, 杜勇. 基于ADS仿真的梳状谱发生器的设计与实现[J]. 电子科技,2014,27(7):84-86. doi: 10.3969/j.issn.1007-7820.2014.07.023LAI H Y, LI G C, DU Y. Design and realization of a comb generator based on the simulation of ADS[J]. Electronic Science and Technology, 2014, 27(7): 84-86. (in Chinese). doi: 10.3969/j.issn.1007-7820.2014.07.023 [33] IEEE. IEEE Std 1139-2022 IEEE standard definitions of physical quantities for fundamental frequency and time metrology--random instabilities[S]. New York: IEEE, 2022: 1-60. [34] RUBIOLA E, VERNOTTE F. The companion of enrico’s chart for phase noise and two-sample variances[J]. IEEE Transactions on Microwave Theory and Techniques, 2023, 71(7): 2996-3025. doi: 10.1109/TMTT.2023.3238267 [35] LIU H SH, LUO Z R, JIN G. The development of phasemeter for Taiji space gravitational wave detection[J]. Microgravity Science and Technology, 2018, 30(6): 775-781. doi: 10.1007/s12217-018-9625-6 [36] LUO Z R, YU T, LIU H SH, et al. The phasemeter of Taiji-1 experimental satellite[J]. International Journal of Modern Physics A, 2021, 36(11n12): 2140005. doi: 10.1142/S0217751X21400054 [37] 张强涛, 刘河山, 罗子人. 面向空间激光干涉的多通道相位测量系统[J]. 中国光学(中英文),2023,16(5):1089-1099. doi: 10.37188/CO.2022-0258ZHANG Q T, LIU H SH, LUO Z R. Multi-channel phase measurement system for the space laser interferometry[J]. Chinese Optics, 2023, 16(5): 1089-1099. doi: 10.37188/CO.2022-0258 -















 下载:
下载: