Optimization of optical metrology noise link metrics for space-based gravitational wave detection spacecraft
-
摘要:
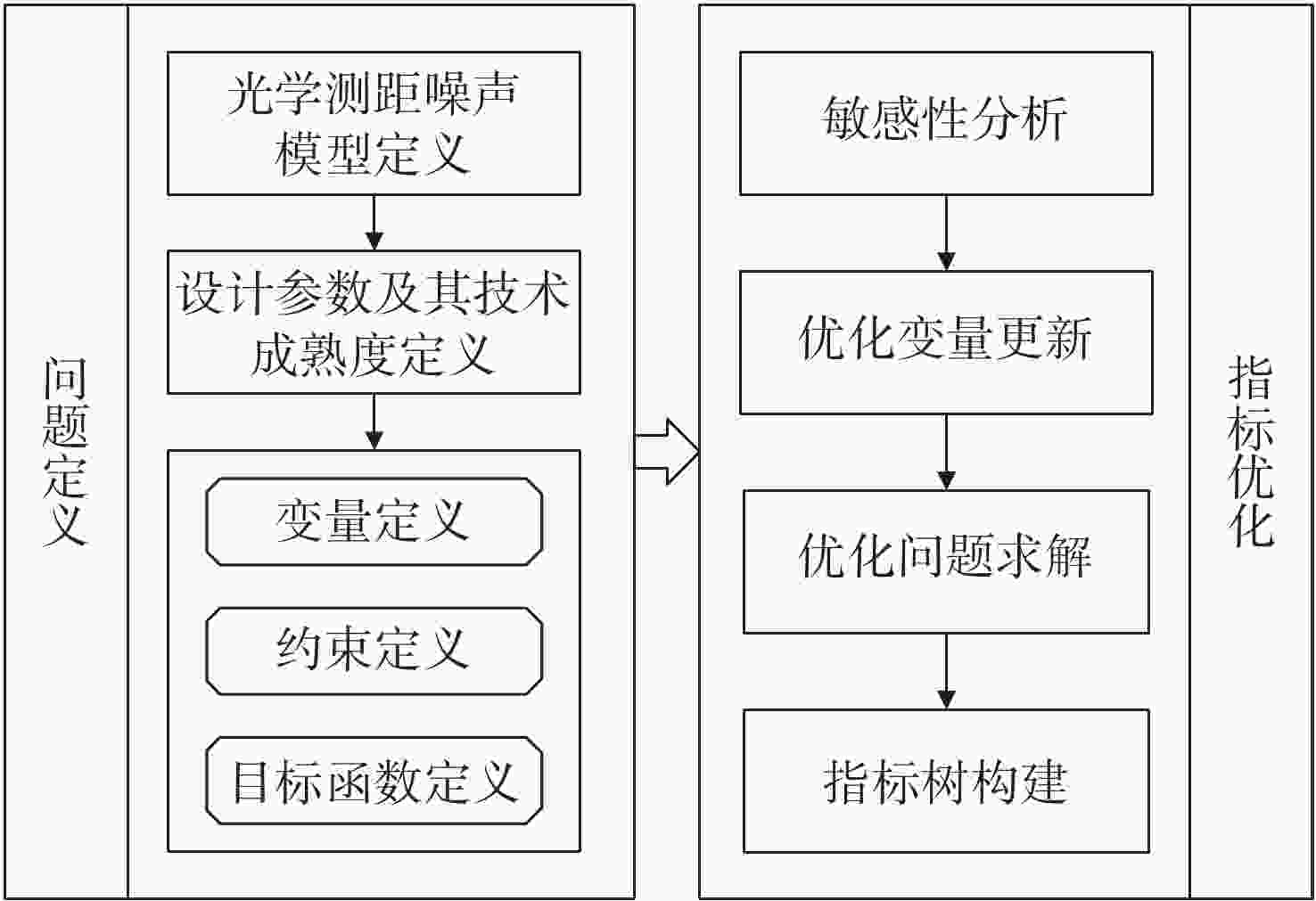
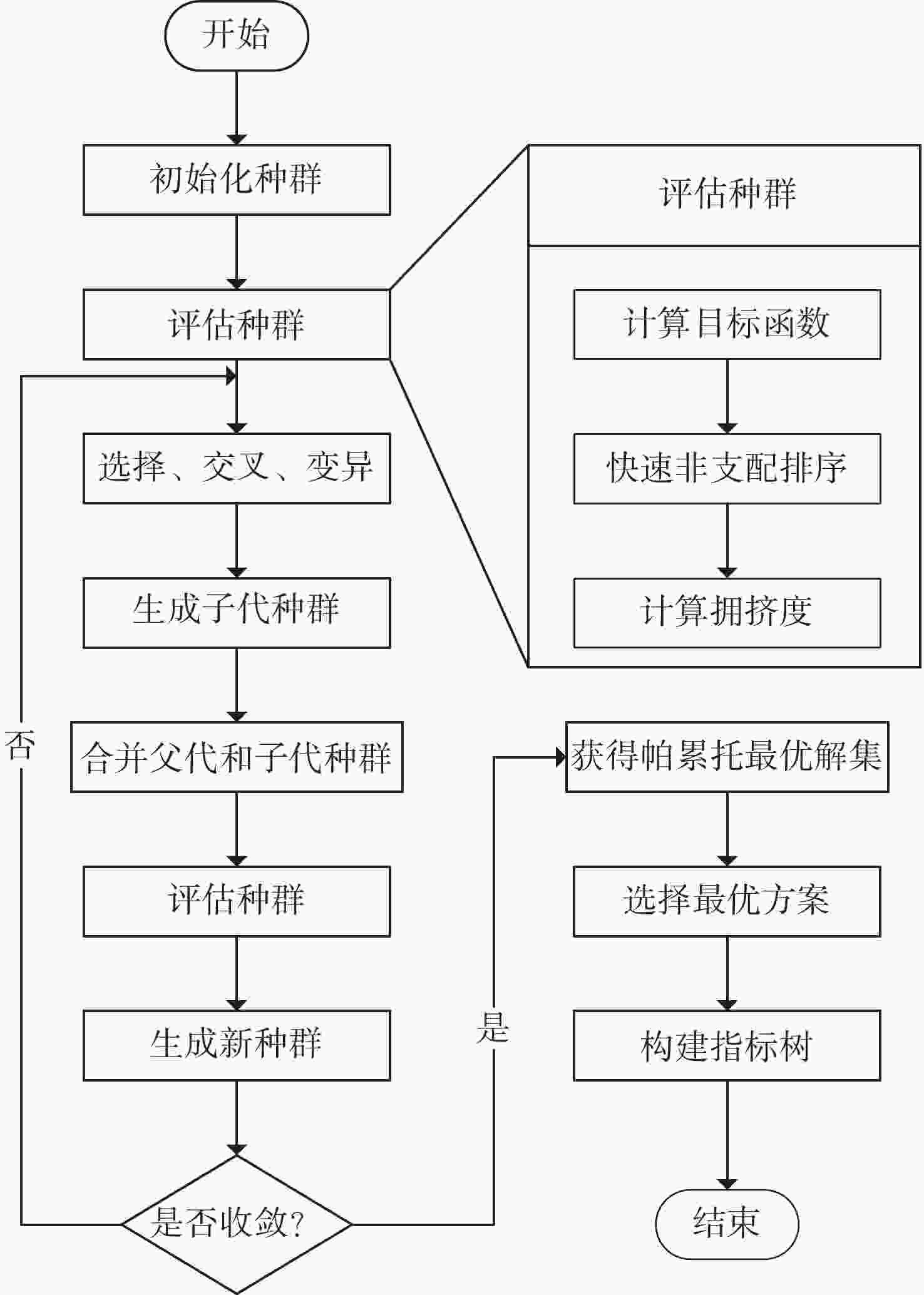
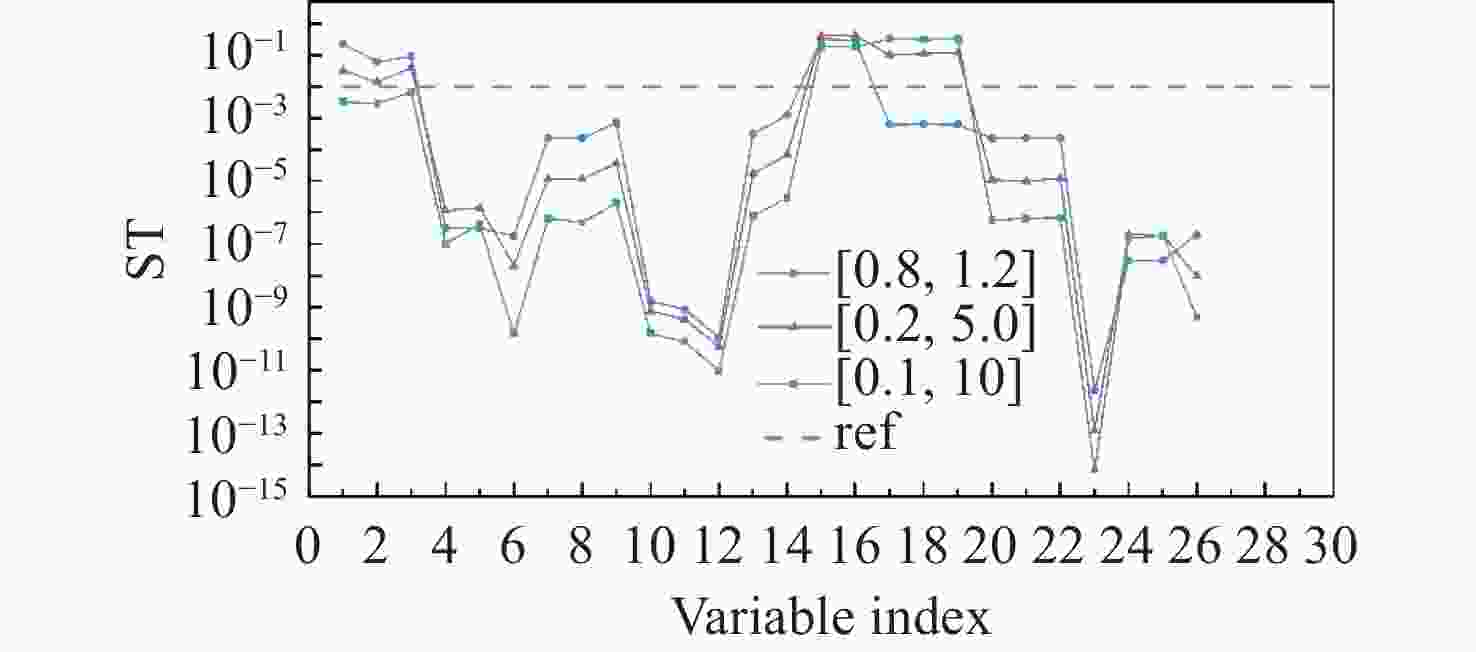
为满足空间引力波探测皮米级测距精度的需求，本文提出了一种星间光学测距噪声链路指标优化方法。该方法通过对设计参数进行优化，在确保星间测距精度的同时提高航天器设计方案的技术可行性。首先，明确优化问题的设计参数及目标函数，结合Sobol敏感性分析有效识别出关键参数。随后，采用非支配排序遗传算法(NSGAII)对优化问题进行求解，从帕累托解集中筛选出符合需求的最优方案。在此基础上，确定各参数的设计指标并初步构建指标树。通过仿真实验验证了方法的可行性。结果表明：采用本文方法优化噪声链路指标，能够在满足
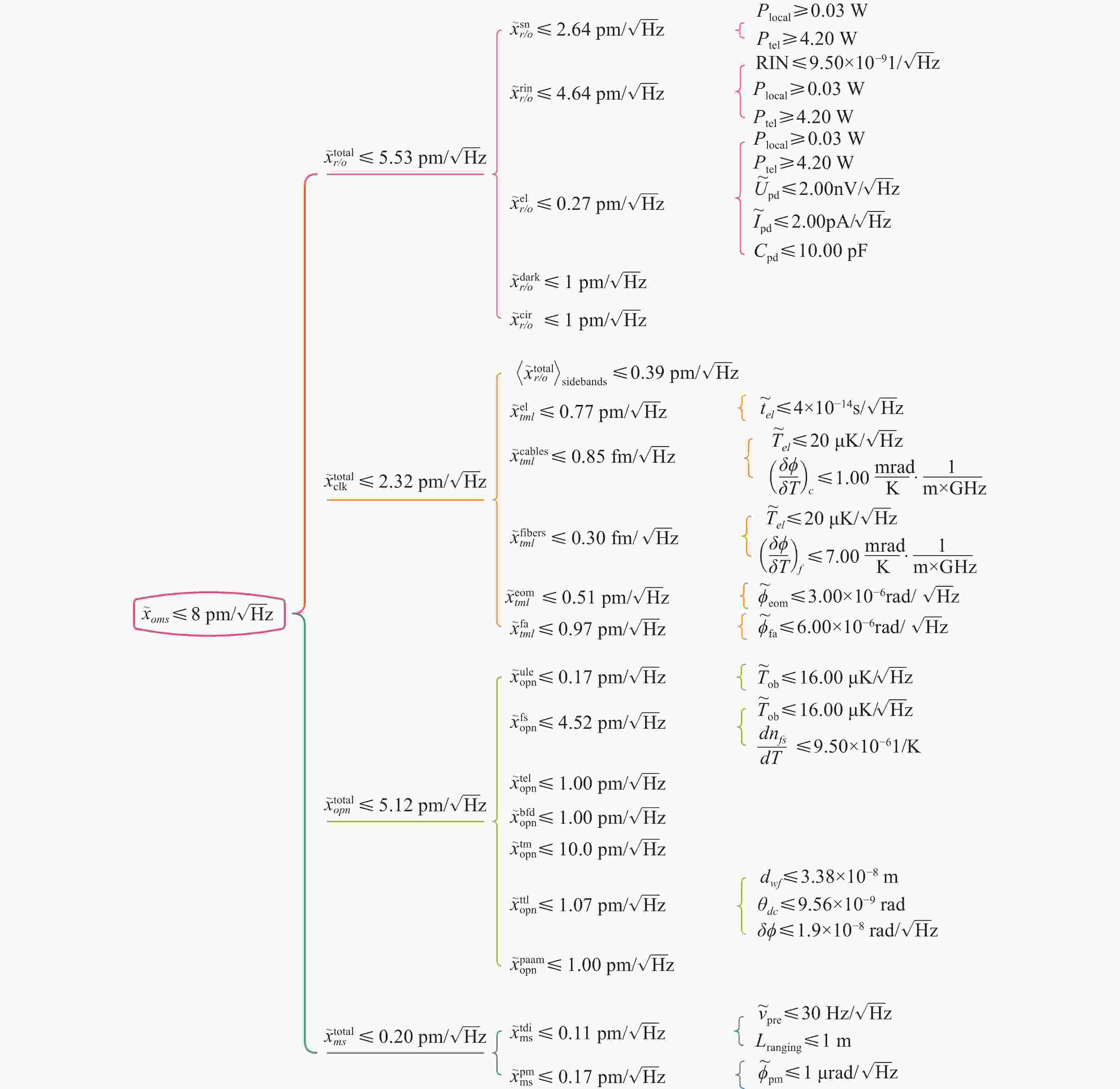
$ 8\;\mathrm{p}\mathrm{m}/\sqrt{\mathrm{H}\mathrm{z}} $ 光学测距噪声要求的同时，获得技术可行性最高的设计方案。本研究为后续航天器设计阶段指标体系的构建提供了有效的参考思路与框架，具有良好的适用性，为未来的引力波探测任务奠定了基础。Abstract:To meet the picometer-level ranging accuracy requirements for space-based gravitational wave detection, this paper proposes an optimization method for the inter-spacecraft optical metrology noise link metrics. The method optimizes the design parameter to ensure the inter-spacecraft ranging accuracy while improving the technical feasibility of the spacecraft design. Firstly, the design parameters and objective functions of the optimization problem are clearly defined, and Sobol sensitivity analysis is used to effectively identify the key parameters. Subsequently, the optimization problem is solved using the Non-dominated Sorting Genetic Algorithm II (NSGA-II), from which the optimal solution is selected from the Pareto front based on the requirements. On this basis, the design metrics for each parameter are determined, and an initial metric tree is constructed. Simulation experiments verify the feasibility of the method. The results show that by optimizing the noise link metrics in accordance with the proposed approach, it is possible to achieve an optical metrology noise level of 8 pm/
$\sqrt{{\mathrm{Hz}}} $ while obtaining the most technically feasible design solution. This study provides a valuable reference framework and approach for the construction of the metric system in the subsequent spacecraft design phase, demonstrating strong applicability and laying the foundation for future gravitational wave detection missions. -
图 3 NSGAII算法求解模型参数优化问题流程
Figure 3. Flowchart of the NSGAII algorithm for solving the model parameter optimization problem
图 10 最优解参数值的相对变化率
Figure 10. Relative variation rate of parameter values for the optimal solution
图 11 非关键参数放松对实施难度指标的影响
Figure 11. Impact of relaxation of non-key parameters on implementation difficulty metric
表 1 任务参数表
Table 1. List of mission parameters
参数 含义 初值 单位 $ {L}_{\rm{arm}} $ 干涉臂长 3×106 km $ {\lambda }_{\rm{laser}} $ 激光器波长 1064 nm $ {n}_{\rm{fs}} $ 熔融石英元件折射率 1.45 N/A $ {f}_{\rm{het}} $ 最大外差频率 1.8 MHz $ {f}_{\rm{mod}} $ 激光调制频率 2.4 GHz $ m $ 调制深度 0.53 N/A $ {N}_{\rm{pd}} $ 光电探测器象限数量 4 N/A $ {d}_{\rm{tel}} $ 望远镜口径 0.4 m $ {OPD}_{\rm{ob}} $ 光学平台上的光程差 565 mm $ {OPD}_{\rm{fs}} $ 熔融石英元件内的光程差 29 mm $ {\alpha }_{\rm{ule}} $ 微晶玻璃的热膨胀系数 2×10−8 1/K $ {\alpha }_{\rm{fs}} $ 熔融石英元件的热膨胀系数 5.5×10−7 1/K $ {l}_{\rm{cables}} $ 电缆长度 2 $ \mathrm{m} $ $ {l}_{\rm{fibers} }$ 光纤长度 5 m $ {\eta }_{\rm{het}} $ 外差检测的效率 0.7 N/A $ {\eta }_{\rm{opt}} $ 接收路径中的光学效率 0.7 N/A $ {\eta }_{\rm{pd}} $ 光电探测器的量子效率 0.8 N/A 
下载: 导出CSV
表 2 读出噪声参数表（1 mHz处）
Table 2. List of readout noise parameters (at 1 mHz)
参数 含义 初值 单位 TRL $ RIN $ 相对强度噪声 1×10−8 $ 1/\sqrt{\mathrm{H}\mathrm{z}} $ 4 $ {P}_{\rm{local}} $ 本地激光功率 0.04 W 5 $ {P}_{\rm{tel}} $ 望远镜出射光功率 4 W 5 $ {C}_{\rm{pd}} $ 光电探测器的电容 10 pF 5 $ {\tilde{U}}_{\rm{pd}} $ 跨阻放大器电压噪声 2 $ \mathrm{n}\mathrm{V}/\sqrt{\mathrm{H}\mathrm{z}} $ 5 $ {\tilde{I}}_{\rm{pd}} $ 跨阻放大器电流噪声 2 $ \mathrm{p}\mathrm{A}/\sqrt{\mathrm{H}\mathrm{z}} $ 5 $ {\tilde{x}}_{r/o}^{\rm{dark}} $ 暗电流噪声 1 $ \mathrm{p}\mathrm{m}/\sqrt{\mathrm{H}\mathrm{z}} $ 2 $ {\tilde{x}}_{r/o}^{\rm{cir}} $ 测量电路噪声 1 $ \mathrm{p}\mathrm{m}/\sqrt{\mathrm{H}\mathrm{z}} $ 2
下载: 导出CSV
表 3 时钟噪声参数表（1 mHz处）
Table 3. List of clock noise parameters (at 1 mHz)
参数 含义 初值 单位 TRL $ {\tilde{t}}_{el} $ 时序抖动噪声 40 $ \mathrm{f}\mathrm{s}/\sqrt{\mathrm{H}\mathrm{z}} $ 3 $ {\tilde{T}}_{el} $ 元件温度噪声 20 $ \text{μ}\mathrm{K}/\sqrt{\mathrm{H}\mathrm{z}} $ 5 $ {\left(\dfrac{\delta \phi }{\delta T}\right)}_{{\mathrm{c}}} $ 电缆温漂系数 7 $ \dfrac{\mathrm{m}\mathrm{r}\mathrm{a}\mathrm{d}}{\mathrm{K}}\dfrac{1}{\mathrm{m}\times \mathrm{G}\mathrm{H}\mathrm{z}} $ 5 $ {\left(\dfrac{\delta \phi }{\delta T}\right)}_{{\mathrm{f}}} $ 光纤温漂系数 1 $ \dfrac{\mathrm{m}\mathrm{r}\mathrm{a}\mathrm{d}}{\mathrm{K}}\dfrac{1}{\mathrm{m}\times \mathrm{G}\mathrm{H}\mathrm{z}} $ 5 $ {\tilde{\phi }}_{\rm{eom}} $ EOM相位噪声 3×10−6 $ \mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ 2 $ {\tilde{\phi }}_{{\mathrm{FA}}} $ FA相位噪声 6×10−6 $ \mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ 2
下载: 导出CSV
表 4 光程噪声参数表（1 mHz处）
Table 4. List of optical path noise parameters (at 1 mHz)
参数 含义 初值 单位 TRL $ {\tilde{T}}_{{ob}} $ 光学平台的温度噪声 20 $ \text{μ}\mathrm{K}/\sqrt{\mathrm{H}\mathrm{z}} $ 5 $ \dfrac{d{n}_{{fs}}}{dT} $ 熔融石英折射率随
温度变化的导数1×10−5 1/K 4 $ {d}_{\rm{wf}} $ 波前畸变 3.55×10−8 m 3 $ {\theta }_{\rm{dc}} $ 角度偏移 1×10−8 rad 5 $ \delta \phi $ 角度抖动 2×10−8 $ \mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ 5 $ {\tilde{x}}_{\rm{opn}}^{\rm{tel}} $ 望远镜光程抖动噪声 1 $ \mathrm{p}\mathrm{m}/\sqrt{\mathrm{H}\mathrm{z}} $ 2 $ {\tilde{x}}_{\rm{opn}}^{\rm{bfd}} $ 光纤延迟噪声 1 $ \mathrm{p}\mathrm{m}/\sqrt{\mathrm{H}\mathrm{z}} $ 2 $ {\tilde{x}}_{\rm{opn}}^{\rm{paam}} $ 光束转向机构噪声 1 $ \mathrm{p}\mathrm{m}/\sqrt{\mathrm{H}\mathrm{z}} $ 2 $ {\tilde{x}}_{\rm{opn}}^{\rm{tm}} $ 检验质量运动噪声 10 $ \mathrm{f}\mathrm{m}/\sqrt{\mathrm{H}\mathrm{z}} $ 2
下载: 导出CSV
表 5 测量系统参数表（1 mHz处）
Table 5. List of measurement noise parameters (at 1 mHz)
参数 含义 初值 单位 TRL $ {\tilde{v}}_{\rm{pre}} $ 激光频率噪声 30 $ \mathrm{H}\mathrm{z}/\sqrt{\mathrm{H}\mathrm{z}} $ 4 $ {L}_{\rm{ranging} }$ 测距误差 1 m 3 $ {\tilde{\phi }}_{\rm{pm}} $ 辅助相位噪声 1 $ \text{μ}\mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ 5
下载: 导出CSV
表 6 技术成熟度等级表（1 mHz处）
Table 6. List of technology readiness levels (at 1 mHz)
TRL 定义 1级 发现和报道了基本原理 2级 提出了技术概念或应用设想 3级 技术应用方案的关键功能或特性
通过了分析与实验室证实4级 在实验室环境下验证了
部件或原理样机的性能5级 部件或原理样机的关键功能
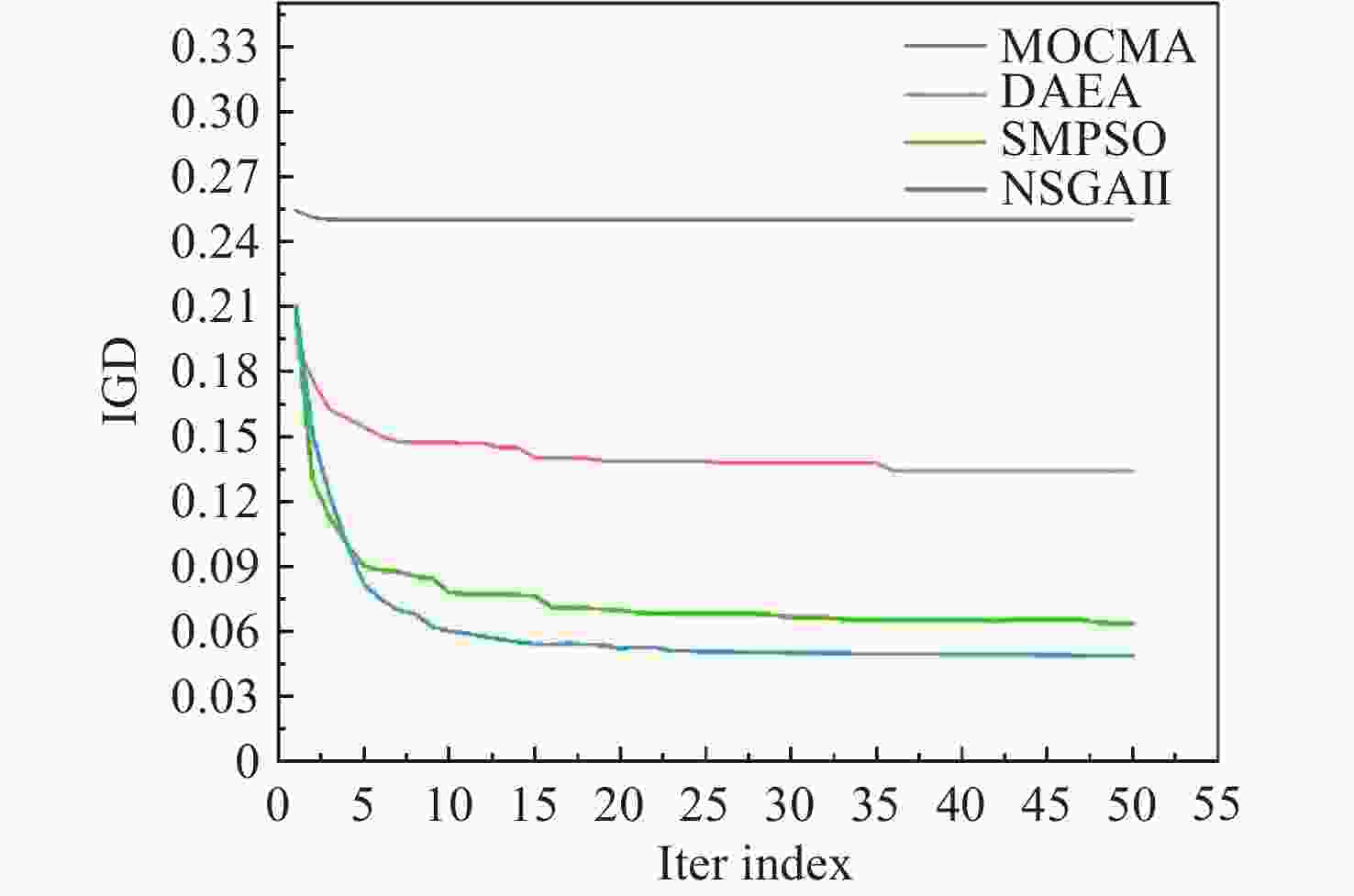
在相关环境下得到了验证
下载: 导出CSV
表 7 各算法优化性能指标对比表
Table 7. Comparison of optimization performance metrics for different algorithms
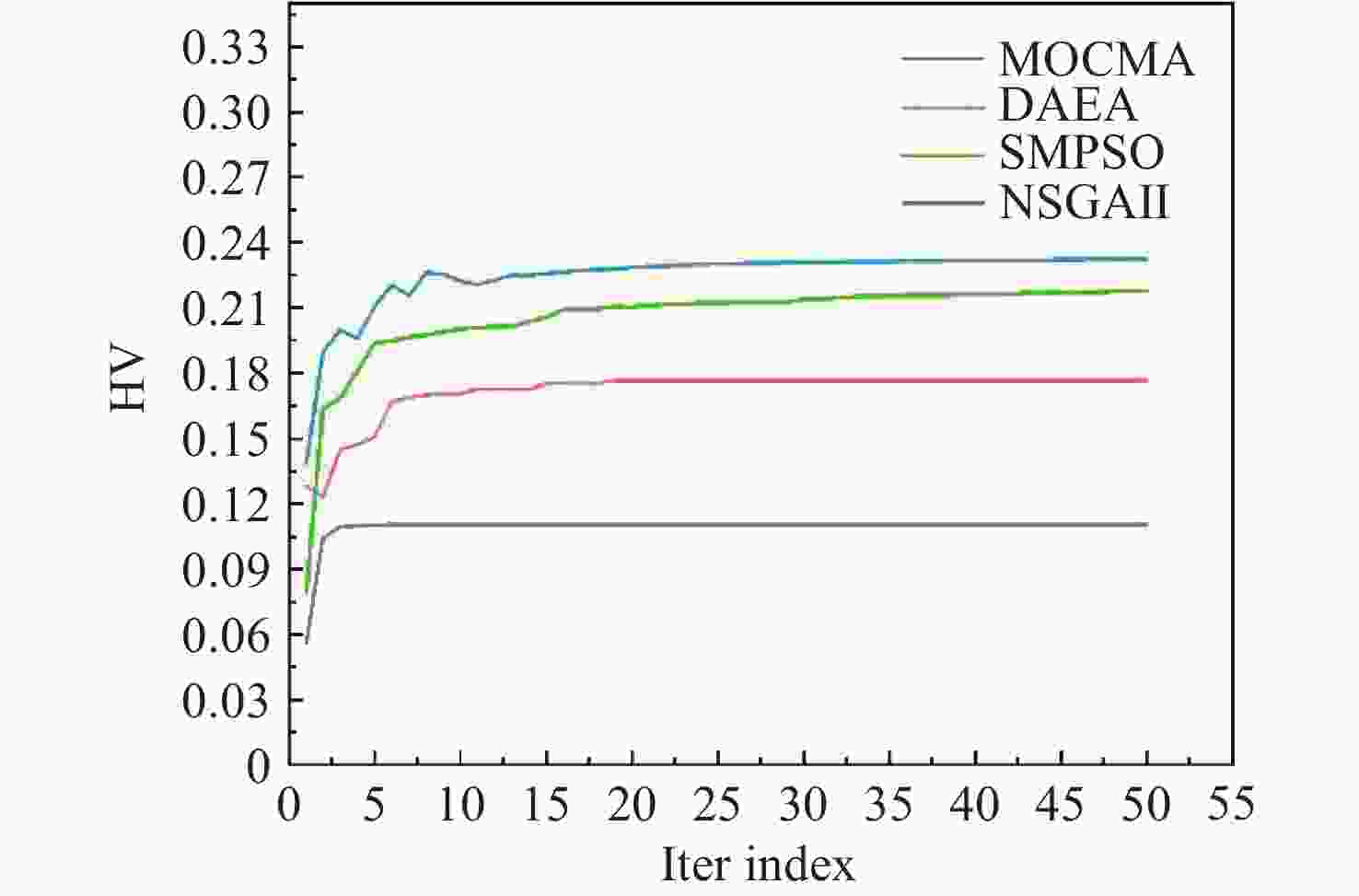
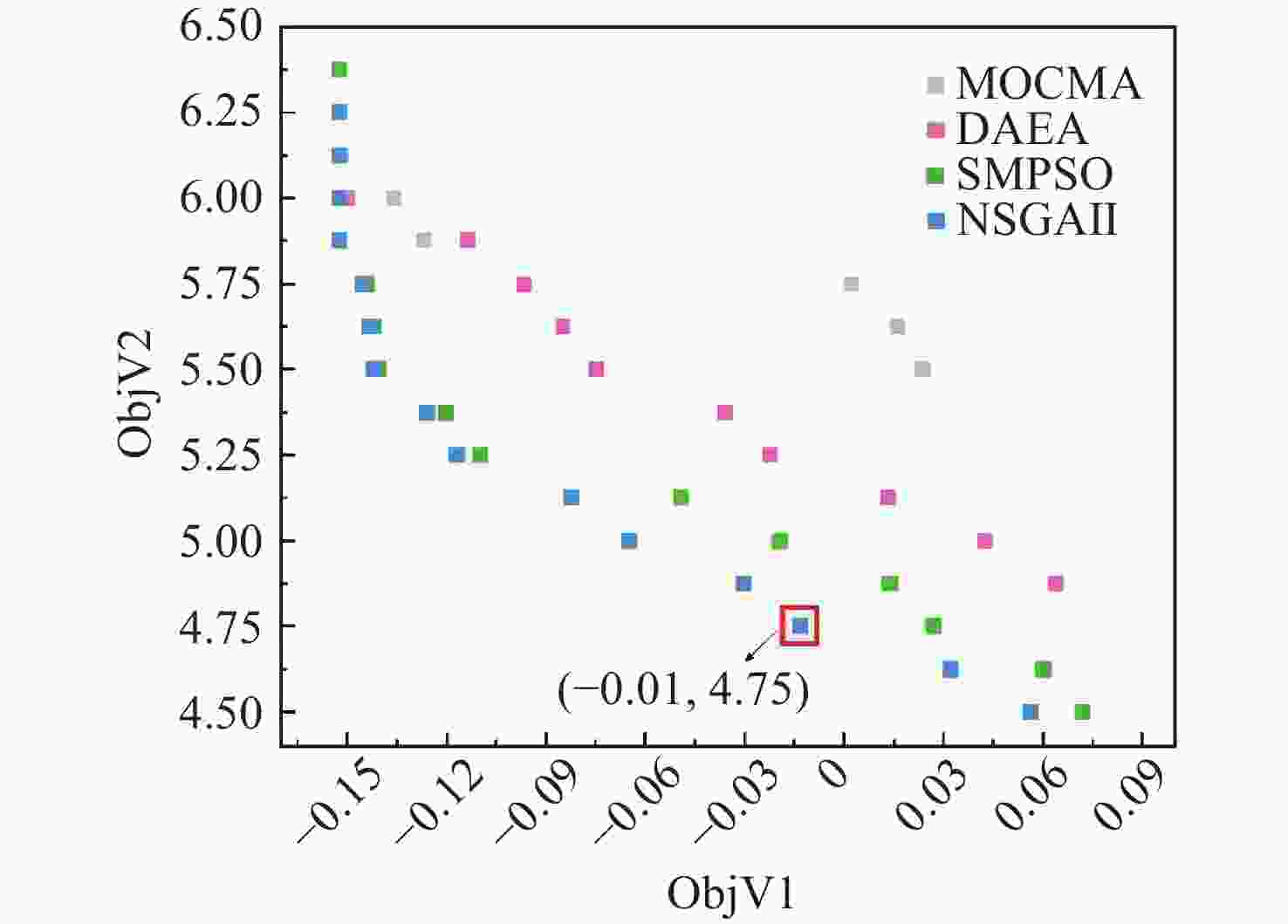
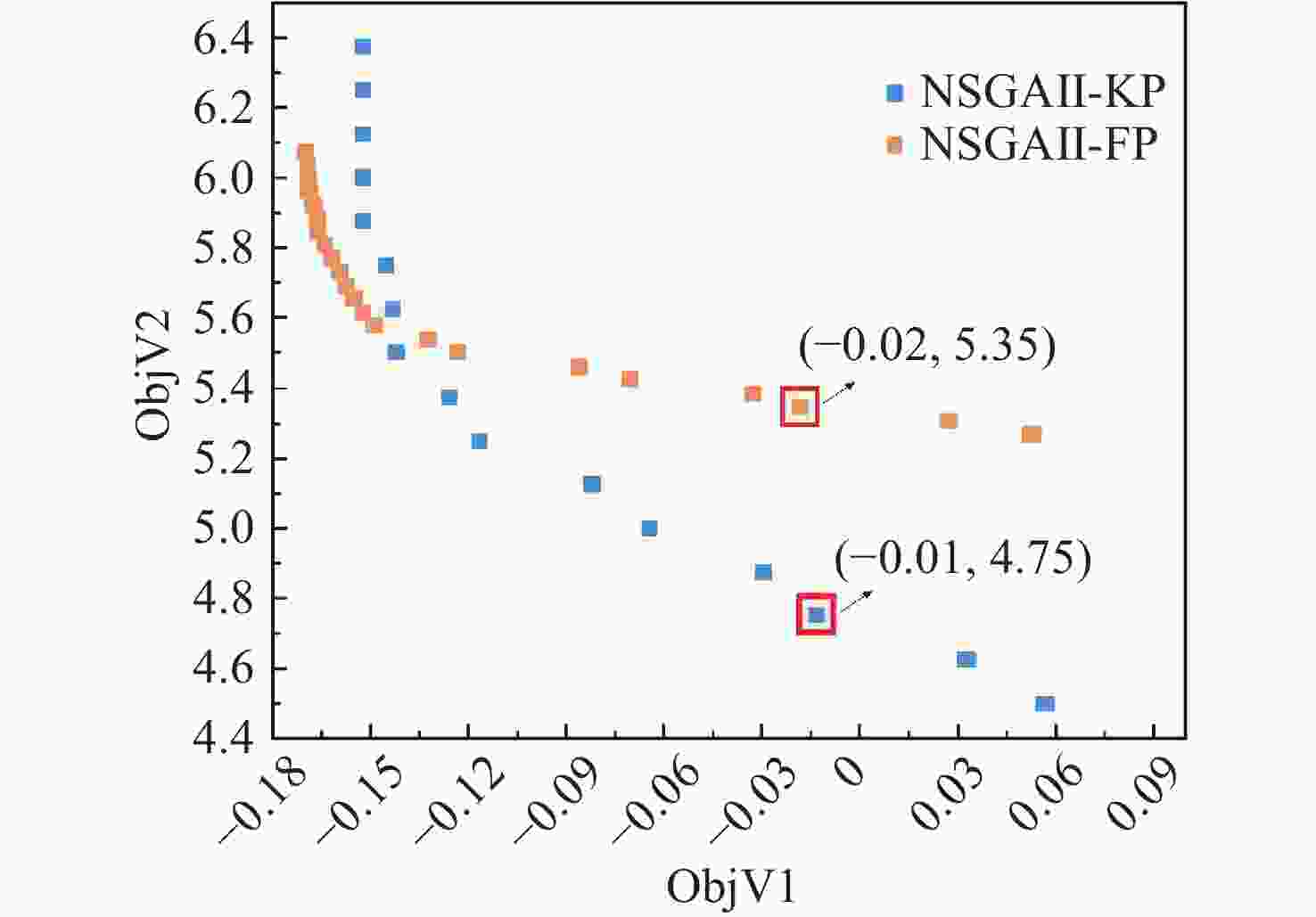
算法 IGD(avg) IGD(std) HV(avg) HV(std) MOCMA 0.2321 0.0268 0.1167 0.0051 DAEA 0.1583 0.0224 0.1649 0.0097 SMPSO 0.0696 0.0059 0.2121 0.0064 NSGAII 0.0488 0.0003 0.2322 0.0002
下载: 导出CSV
表 8 关键参数指标优化结果表
Table 8. Optimization results of key parameter metrics
参数 初值 初始
TRL优化结果 优化后
TRL单位 指标 $ RIN $ 1×10−8 4 9.50×10−9 4 $ 1/\sqrt{\mathrm{H}\mathrm{z}} $ $ RIN\leqslant 9.50 $×10−9 $ {P}_{\rm{local}} $ 0.04 5 0.032 5 W $ {P}_{\rm{local}}\geqslant 0.032 $ $ {P}_{\rm{tel}} $ 4 5 4.197 5 W $ {P}_{\rm{tel}}\geqslant 4.197 $ $ {\tilde{T}}_{\rm{ob}} $ 20 5 16 3 $ \text{μ}\mathrm{K}/\sqrt{\mathrm{H}\mathrm{z}} $ $ {\tilde{T}}_{\rm{ob}}\leqslant 1.60 $×10−5 $ \dfrac{d{n}_{\rm{fs}}}{dT} $ 1×10−5 4 9.50×10−6 4 1/K $ \dfrac{d{n}_{\rm{fs}}}{dT}\leqslant $9.50×10−6 $ {d}_{\rm{wf}} $ 3.55×10−8 3 3.38×10−8 3 m $ {d}_{\rm{wf}}\leqslant 3.38 $×10−8 $ {\theta }_{\rm{dc}} $ 1×10−8 5 9.56×10−9 5 rad $ {\theta }_{\rm{dc}}\leqslant 9.56 $×10−9 $ \delta \phi $ 2×10−8 5 1.90×10−8 5 $ \mathrm{r}\mathrm{a}\mathrm{d}/\sqrt{\mathrm{H}\mathrm{z}} $ $ \delta \phi \leqslant 1.90 $×10−8
下载: 导出CSV
-
[1] DANZMANN K, RÜDIGER A. LISA technology—concept, status, prospects[J]. Classical and Quantum Gravity, 2003, 20(10): S1-S9. doi: 10.1088/0264-9381/20/10/301 [2] LUO Z R, GUO Z K, JIN G, et al. A brief analysis to Taiji: science and technology[J]. Results in Physics, 2020, 16: 102918. doi: 10.1016/j.rinp.2019.102918 [3] LUO J, CHEN L SH, DUAN H Z, et al. TianQin: a space-borne gravitational wave detector[J]. Classical and Quantum Gravity, 2016, 33(3): 035010. doi: 10.1088/0264-9381/33/3/035010 [4] BAILES M, BERGER B K, BRADY P R, et al. Gravitational-wave physics and astronomy in the 2020s and 2030s[J]. Nature Reviews Physics, 2021, 3(5): 344-366. doi: 10.1038/s42254-021-00303-8 [5] PITKIN M, REID S, ROWAN S, et al. Gravitational wave detection by interferometry (ground and space)[J]. Living Reviews in Relativity, 2011, 14(1): 5. doi: 10.12942/lrr-2011-5 [6] BOND C, BROWN D, FREISE A, et al. Interferometer techniques for gravitational-wave detection[J]. Living Reviews in Relativity, 2016, 19(1): 3. doi: 10.1007/s41114-016-0002-8 [7] PRINCE T A, TINTO M, LARSON S L, et al. LISA optimal sensitivity[J]. Physical Review D, 2002, 66(12): 122002. doi: 10.1103/PhysRevD.66.122002 [8] BORWANKAR P, KAPANIA R K, INOYAMA D, et al. Multidisciplinary design analysis and optimization of space vehicle structures[C]. Proceedings of the AIAA SCITECH 2024 Forum, AIAA, 2024: 2898. [9] ISAJI M, TAKUBO Y, HO K. Multidisciplinary design optimization approach to integrated space mission planning and spacecraft design[J]. Journal of Spacecraft and Rockets, 2022, 59(5): 1660-1670. doi: 10.2514/1.A35284 [10] LEE D Y. Multidisciplinary optimization approach for design and operation of constrained and complex-shaped space systems[D]. Ann Arbor: University of Michigan, 2016. [11] LIU CH R, XU ZH B, HAN K, et al. Optimization design of core ultra-stable structure for space gravitational wave detection satellite based on response surface methodology[J]. Aerospace, 2024, 11(7): 518. doi: 10.3390/aerospace11070518 [12] SONG J, FAN W T, FANG S J, et al. Optimized design of a gravitational wave telescope system based on pupil aberration[J]. Applied Optics, 2024, 63(7): 1815-1821. doi: 10.1364/AO.515579 [13] 房思俊, 李博宏, 何斌, 等. 空间引力波望远镜主镜组件结构设计及热稳定性分析[J]. 光电工程,2024,51(2):230157.FANG S J, LI B H, HE B, et al. Design and thermal stability analysis of primary mirror assembly for space-borne gravitational wave telescope[J]. Opto-Electronic Engineering, 2024, 51(2): 230157. (in Chinese). [14] 李博宏, 罗健, 丘敏艳, 等. 引力波探测望远镜超低热变形桁架支撑结构设计技术[J]. 光电工程,2023,50(11):230155.LI B H, LUO J, QIU M Y, et al. Design technology of the truss support structure of the ultra-low thermal deformation gravitational wave detection telescope[J]. Opto-Electronic Engineering, 2023, 50(11): 230155. (in Chinese). [15] 潘宇倩, 冯文婧, 张弓, 等. 导航卫星自主健康管理指标体系构建方法[J]. 航天器工程,2021,30(4):8-14. doi: 10.3969/j.issn.1673-8748.2021.04.002PAN Y Q, FENG W J, ZHANG G, et al. Construction method of navigation satellite health management evaluation index system[J]. Spacecraft Engineering, 2021, 30(4): 8-14. (in Chinese). doi: 10.3969/j.issn.1673-8748.2021.04.002 [16] 谢军, 张建军, 王岗. 北斗卫星导航系统测量误差指标体系[J]. 宇航学报,2018,39(9):977-985. doi: 10.3873/j.issn.1000-1328.2018.09.005XIE J, ZHANG J J, WANG G. Measurement error index system of Bei Dou satellite navigation system[J]. Journal of Astronautics, 2018, 39(9): 977-985. (in Chinese). doi: 10.3873/j.issn.1000-1328.2018.09.005 [17] 朱伊明, 张玉珠, 陈斌, 等. 基于MBSE的空间引力波探测系统指标管理及其探测灵敏度分析[J]. 图学学报,2024,45(2):259-267.ZHU Y M, ZHANG Y ZH, CHEN B, et al. Space gravitational wave detection parameter management and performance analysis based on MBSE[J]. Journal of Graphics, 2024, 45(2): 259-267. (in Chinese). [18] LUO Z R, WANG Y, WU Y L, et al. The Taiji program: a concise overview[J]. Progress of Theoretical and Experimental Physics, 2021, 2021(5): 05A108. doi: 10.1093/ptep/ptaa083 [19] 王娟, 齐克奇, 王少鑫, 等. 面向空间引力波探测的激光干涉技术研究进展及展望[J]. 中国科学: 物理学 力学 天文学, 2024, 54(7): 270405.WANG J, QI K Q, WANG SH X, et al. Advance and prospect in the study of laser interferometry technology for space gravitational wave detection[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2024, 54(7): 270405. (in Chinese). [20] BARKE S. Inter-spacecraft frequency distribution for future gravitational wave observatories[D]. Hannover: Gottfried Wilhelm Leibniz Universität Hannover, 2015. [21] KULKARNI S A. Technology development for ground verification of dimensional stability of the LISA telescope[D]. Gainesville: University of Florida, 2022. [22] FLEDDERMANN R, DIEKMANN C, STEIER F, et al. Sub-pm $ \sqrt{\mathrm{Hz}}^{-1} $ non-reciprocal noise in the LISA backlink fiber[J]. Classical and Quantum Gravity, 2018, 35(7): 075007. doi: 10.1088/1361-6382/aaa276[23] WANNER G, KARNESIS N. Preliminary results on the suppression of sensing cross-talk in LISA Pathfinder[J]. Journal of Physics: Conference Series, 2017, 840(1): 012043. [24] PIJNENBURG J A C M, RIJNVELD N. Picometer stable scan mechanism for gravitational wave detection in space: LISA PAAM[J]. Proceedings of SPIE, 2017, 10565: 105652Z. [25] BENDER P L. Wavefront distortion and beam pointing for LISA[J]. Classical and Quantum Gravity, 2005, 22(10): S339-S346. doi: 10.1088/0264-9381/22/10/027 [26] IGEL C, HANSEN N, ROTH S. Covariance matrix adaptation for multi-objective optimization[J]. Evolutionary Computation, 2007, 15(1): 1-28. doi: 10.1162/evco.2007.15.1.1 [27] XU H, XUE B, ZHANG M J. A duplication analysis-based evolutionary algorithm for biobjective feature selection[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(2): 205-218. doi: 10.1109/TEVC.2020.3016049 [28] NEBRO A J, DURILLO J J, GARCIA-NIETO J, et al. SMPSO: a new PSO-based metaheuristic for multi-objective optimization[C]. Proceedings of the IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making, IEEE, 2009: 66-73. [29] COELLO C A C, CORTÉS N C. Solving multiobjective optimization problems using an artificial immune system[J]. Genetic Programming and Evolvable Machines, 2005, 6(2): 163-190. doi: 10.1007/s10710-005-6164-x [30] ZITZLER E, THIELE L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J]. IEEE Transactions on Evolutionary Computation, 1999, 3(4): 257-271. doi: 10.1109/4235.797969 -
下载:
计量
- 文章访问数: 102
- HTML全文浏览量: 30
- PDF下载量: 9
- 被引次数: 0
