Measurement of large off-axis convex asphere by systemic stitching testing method
-
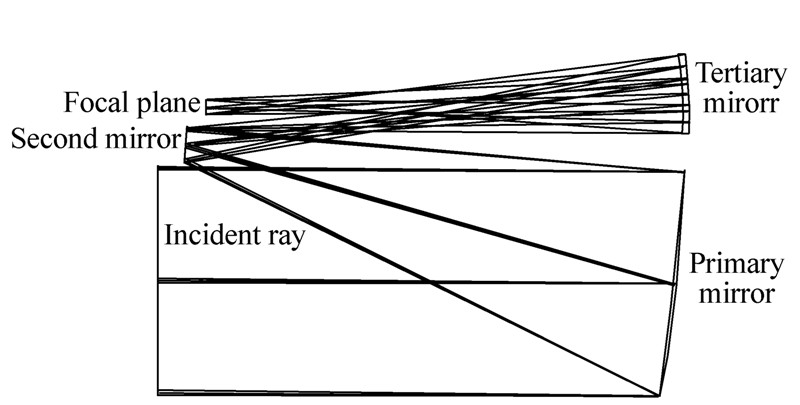
摘要: 针对大口径离轴凸非球面面形检测的困难,本文将光学系统波像差检验技术与子孔径拼接干涉技术相结合,提出了凸非球面系统拼接检测方法。对该方法的基本原理和具体实现过程进行了分析和研究,并建立了合理的子孔径拼接数学模型。当离轴三反光学系统的主镜和三镜加工完成以后,对整个系统进行装调和测试,并依次测定光学系统各视场的波像差分布,通过综合优化子孔径拼接算法和全口径面形数据插值可以求解得到大口径非球面全口径的面形信息,从而为非球面后续加工和系统的装调提供了依据和保障。结合工程实例,对一口径为287 mm×115 mm的离轴非球面次镜进行了系统拼接测试和加工,经过两个周期的加工和测试,其面形分布的RMS值接近1/30λ(λ=632.8 nm)。Abstract: In order to overcome the difficulty of testing large off-axis convex asphere, the convex asphere systemic stitching testing method combining with wave aberration testing and subaperture stitching interferometry(SSI) is proposed.The basic principle and flow chart of this method are analyzed and researched, and the stitching mathematical model is established.When the primary mirror and second mirror of the three mirror astigmatism(TMA) system have been fabricated, we align and calibrate the optical system, and test wave aberration of all the fields successively.Then we can obtain the phase map of the whole aperture by the synthetical optimization stitching algorithm and interpolation, which provides the guarantee of the subsequent fabrication and systemic testing.With engineering examples, a large convex mirror with the aperture of 287 mm×115 mm is tested by the method, and the value of RMS of the surface error is close to 1/30λ(λ=632.8 nm) after two cycles of fabricating and testing.
-
-
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] -






 下载:
下载: